一、路由选择算法概述
- 路由选择算法的目标:找到“从源节点到目的节点的最低开销路径”
- 路由选择算法的第一种分类
- centralized routing algorithm集中式路由选择算法
- 集中式路由选择算法需要计算者具有“网络拓扑的全局连通性”和“全局链路开销”方面的完整信息。
- 具有全局状态信息的算法又被称作链路状态算法——Link State(LS)算法,即该算法必须知道网络中每条链路的开销。
- 代表算法——Dijkstra-Link-State算法
- decentralized routing algorithm分散式路由选择算法
- 路由器以迭代、分布式的方式计算出最低开销路径。
- 没有节点拥有关于所有网络链路开销的完整信息,相反,每个节点仅有与其直接相连链路的开销信息便可开始工作。
- 通过迭代计算及相邻节点间的信息交换,一个节点逐渐计算出到达某个目的节点的最低开销路径。
- 代表算法——Distance-Vector距离向量算法,之所以叫DV算法,是因为每个节点维护到网络中所有其他节点的开销估计向量。
- centralized routing algorithm集中式路由选择算法
- 路由选择算法的第二种分类
- 静态路由选择算法
- 人工调整路由
- 动态路由选择算法
- 随着网络流量负载或拓扑发生变化而改变路由选择路径。
- 静态路由选择算法
- 路由选择算法的第三种分类:负载敏感/迟钝
- 负载敏感算法
- 负载敏感算法认为:在网络中,链路开销会动态地反映出底层链路当前的拥塞水平。
- 若当前拥塞的一条链路与高开销相联系,则路由选择算法趋向于绕开该拥塞链路来选择路由,如早期的ARPAnet。
- 负载迟钝算法
- 负载迟钝算法认为:某条链路的开销无法明确地反映链路当前或最近的拥塞水平。
- 如RIP、OSPF、BGP算法。
- 负载敏感算法
二、Dijkstra算法原理【注意:我们直接通过实例来学习该算法】
2.1 Dijkstra算法原理
- Dijkstra算法属于链路状态LS算法
- 在链路状态算法中,需要“用作LS算法输入”的“网络拓扑”和“所有的链路开销”都是透明已知的。
- 实践中,为了让上述信息成为透明已知,可通过让网络中的每个节点向网络中所有其他节点广播链路状态分组来实现。其中每个链路状态分组包含该节点所连接的链路的标识和开销。节点广播的结果是:网络中所有节点都具有该网络的“统一、完整的拓扑及开销视图”,因此每个节点都能够运行LS算法并计算出相同的最低开销路径集合。
- Dijkstra算法同时属于迭代算法
- 经过算法的第k次迭代后,可知晓“到k个目的节点的最低开销路径”
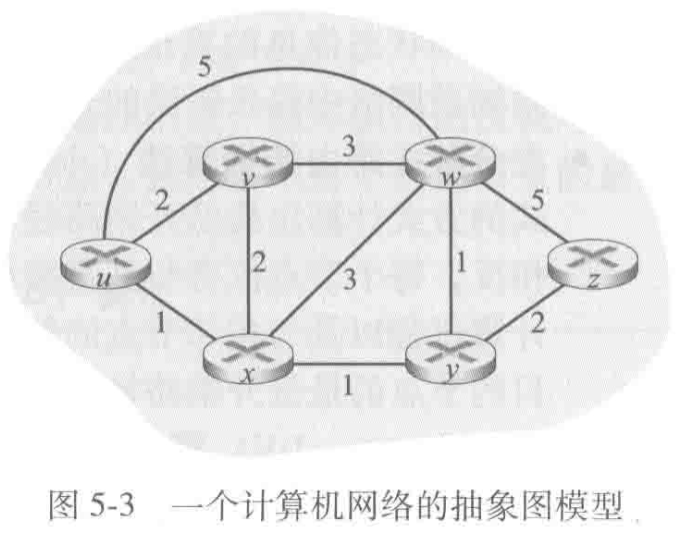
- 实例网络拓扑【LS算法中拓扑结构和链路开销都是透明已知的】
2.1.1 符号说明
- D(a):到算法的本次迭代,从源节点到目的节点a的“最低开销路径”的总开销
- p(a):当前“源节点到a节点的最短开销路径”的a节点的前一节点
- N':节点子集;如果从源节点到a节点的最低开销路径已确定,则将a节点放入节点子集N'
- c(a,b):若“a adj b”(两节点相邻),则“c(a,b) = 两节点之间的开销”,否则“c(a,b) = ∞”
2.1.2 网络拓扑中,源节点 u 的Dijkstra链路状态算法(伪代码)示例
# Initialization:即初始化,同时也是一次迭代,统计出源节点到所有邻接节点的开销
N' = {u}
for all nodes a: # “a”泛指所有目的节点if a is neighbor of uD(a) = c(u,a)elseD(a) = ∞
# 迭代内容
while N' != N: # 如果源节点到所有目的节点的最低开销路径没有确定,则持续迭代计算if(s not in N' && D(s) is minimum): # “s”特指在当前一轮迭代计算后,从源到所有目的节点路径开销最小的那个目的节点add s to N'update D(a) for each neighbor ‘a’ of ‘s’ and not in N':D(a) = min(D(a), D(s)+c(s,a)) # 此处为算法核心点,需要注意D(a)、D(s)、c(s,a)的定义!
2.1.3 实例计算表格如下

- 初始化后:源节点 u 到每个目的节点a(a=v、w、x、y、z)的初始最低开销显示在步骤0一行。可以看到,由于节点v、w、x与源节点u相邻,故其链路开销为拓扑图中链路上的具体值;节点y、z不与源节点u相邻,故其链路开销暂且为 ∞ 。同时,由p(a)定义可知,当前的p(v)、p(w)、p(x)均为u。在所有D(a)中,D(x)值最小,因此将节点x放入节点子集N'中。
- 第一次迭代:依据计算公式
D(a) = min(D(a), D(s)+c(s,a))及网络拓扑,其中公式中的s为节点x,我们可以得到第一次迭代后的“源节点到各目的节点的”最低开销D(a)(a=v、w、y、z)。同时,由p(a)定义可知,当前的p(v)=u、p(w)=x、p(y)=x,以p(w)=x为例,这表明当前从源节点到节点w的最短路径为“u->x->w”。在所有D(a)中,D(v)和D(y)值最小,因此我们任选其一,将节点y放入节点子集N'中。 - 第二次迭代:同第一次迭代。
- ......
- 第五次迭代:由于(N' = N),因此退出迭代。最终形成“从源节点到各目的节点的最低开销”D(a)a(a=v、w、x、y、z)以及从源节点到各目的节点的最低开销路径。
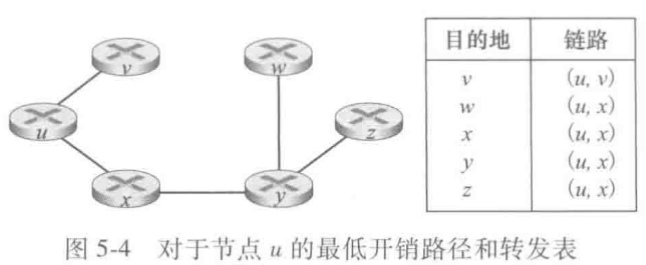
- 以节点w为例:最终D(W)=3意味着“从源节点u到节点w的最低开销”为3,同时,p(w)=y,意味着在“从源节点u到节点w的最低开销路径”中,节点w的上一节点为节点y;我们再观察最终的p(y)=x,可知道在“从源节点u到节点y的最低开销路径”中,节点y的上一节点为节点x;我们再观察最终的p(x)=u,可知道在“从源节点u到节点x的最低开销路径”中,节点x的上一节点为节点u(源节点);综上,从源节点u到目的节点w的最低开销路径为“u->x->y->w”。以此种方式,我们便可以构建从源节点到所有目的节点的最低开销路径。
- 我们在每个节点中均使用该算法,因此每个节点都会形成最低开销路径图及转发表,同时,我们将计算结果分发到网络中的其他节点中用于形成其他节点的路由表(本文重点在于路由算法的讲解,结果分发方式及路由表的建立待更新详解)。以节点u为例,经过计算后,节点u内部生成的最低开销路径图及转发表如下
2.1.4 算法复杂度
$O(\frac {n(n+1)}{2})$ = $O(\ n^{2})$,即每轮迭代计算的节点个数由n依次递减。
2.1.5 算法本身存在的问题及解决方法
- 拥塞敏感的路由选择的震荡(待详解)
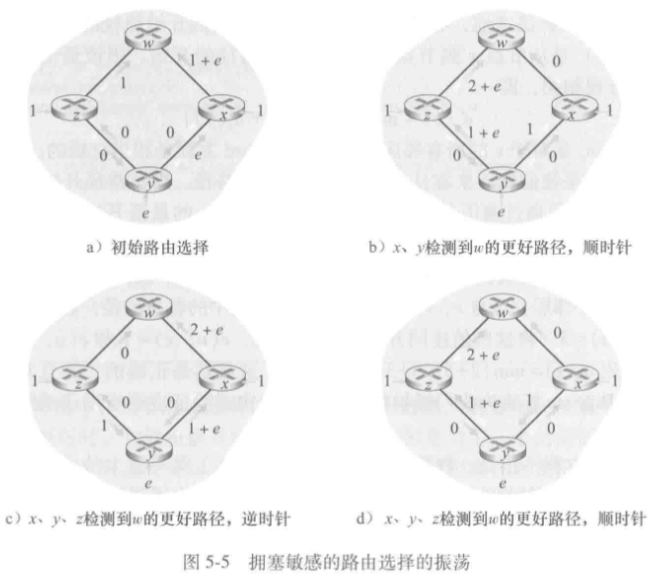
- 解决方案:通过“让每台路由器发送链路通告的时间随机化”,避免路由器自同步运行LS算法,即可确保所有路由器不同时运行LS算法,
三、Distance-Vector距离向量路由选择算法原理
3.1 Distance-Vector算法原理
- 介绍DV算法前,讨论存在于最低开销路径的开销之间的一种重要关系——Bellman-Ford方程
$d_x(y) = min_v[c(x,v)+d_v(y)]$- $d_x(y)$:从节点x到节点y的最低开销路径的实际开销
- v:指$d_x(y)$中下标节点x的所有邻居节点
- $min_v$:该最小函数是对x的所有相邻节点v而言的
3.1.1 Distance-Vector算法特点
- 迭代计算:计算过程持续到相邻节点间无更多信息要交换,要注意,该算法没有计算应该停止的信号,即为自我终止。
- 异步计算:不要求所有节点的计算过程同步。
- 分布式计算:每个节点都要从一个或多个直接相邻节点接收信息执行计算,并将计算结果分发给相邻节点。
3.1.2 Distance-Vector算法基本思想
- 每个节点x维护下列路由选择信息
- $c(x,v)$:从节点x到所有直接相连邻居v的开销
- $\overline{D_x}=[D_x(y):y \in N]$:其中,$\overline{D_x}$是从x到N中所有其他节点y的开销估计向量。该向量包含了节点x到N中所有目的地y的开销估计值,N即为网络中的节点集,
- $\overline{D_v}=[D_v(y):y \in N]$:节点x同时存储维护每个邻居的距离向量
- 在该分布式、异步算法中,每个节点不时地向它的邻居发送它的距离向量副本。
- 当节点x从它的任何一个邻居v接收到一个新的距离向量$\overline{D_v}=[D_v(y):y \in N]$后,节点x使用Bellman-Ford方程更新节点x自己的距离向量:$D_x(y) = min_v[c(x,v)+D_v(y)]$
- 若节点x的距离向量因更新步骤而发生改变,则节点x接下来将向它的所有邻居发送自己更新后的距离向量,这将使所有邻居更新邻居们自己的距离向量。
- 按照上述方式不断进行异步交换距离向量,每个开销估计值$D_x(y)$均会收敛到$d_x(y)$,$d_x(y)$为从节点x到节点y的实际最低开销路径的开销。
3.1.3 距离向量(DV)算法伪代码描述

- 注意:为了更新节点x的转发表,节点x真正需要知道的不是到目的节点y的最低开销路径的开销值,而是从节点x沿着最低开销路径到目的节点y的下一跳邻居节点$v*(y)$。该下一跳路由节点$v(y)$即为在DV伪代码算法的第14行中取得最小值的邻居节点v(若有多个取得最小值的邻居v,则任取一个最小值邻居节点v)。因此,在伪代码的第13~14行,节点x同时决定$v^(y)$并更新节点x对目的地y的转发表。
3.1.4 LS与DV算法的简要区别
- LS算法是一种全局算法,即LS算法要求每个节点在运行Dijkstra算法前,首先需要获得该网络的完整信息。
- DV算法是分布式的,该算法不需要全局信息,节点具有的唯一信息是它到直接相连邻居的链路开销及它从邻居中接收到的信息。每个节点等待来自任何邻居的更新(伪代码第1011行),当接收到一个新的更新时,节点计算它的新距离向量并向它的邻居通告其新距离向量(伪代码第1617行)。
- 实践中,许多类似DV的算法被用于多种路由选择协议中,包括RIP、BGP及早期的ARPAnet。
3.2 Distance-Vector算法运行实例
- 实例中,算法的运行以同步的方式显示,即所有节点同时从其邻居接收报文,计算其新距离向量,如果距离向量发生了变化则通知其邻居节点。异步的方式同样也能正确运行,即异步方式中可在任意时刻出现节点计算与“更新的产生和接收”。
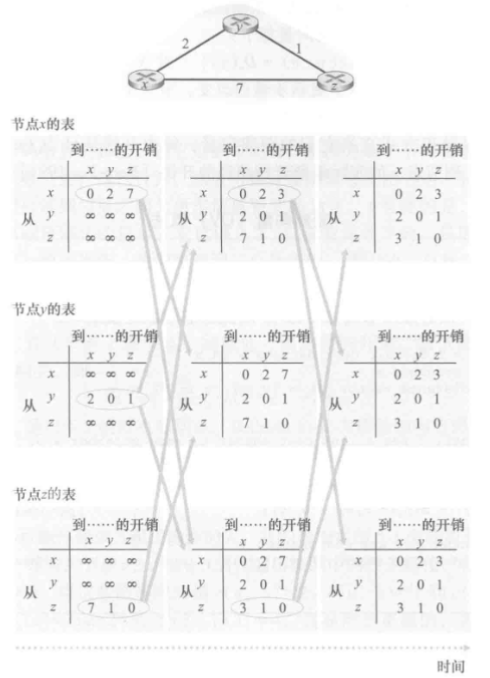
- 注意:当各节点中D(a)计算值不发生改变时,节点停止发送更新通告进入静止等待状态,当链路开销发生改变时,节点计算再次启动。
3.2.1 链路开销发生改变的情况
- 链路开销减少实例
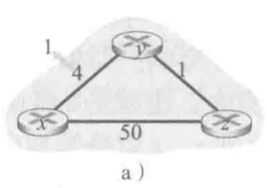
- 节点链路开销表变化如下
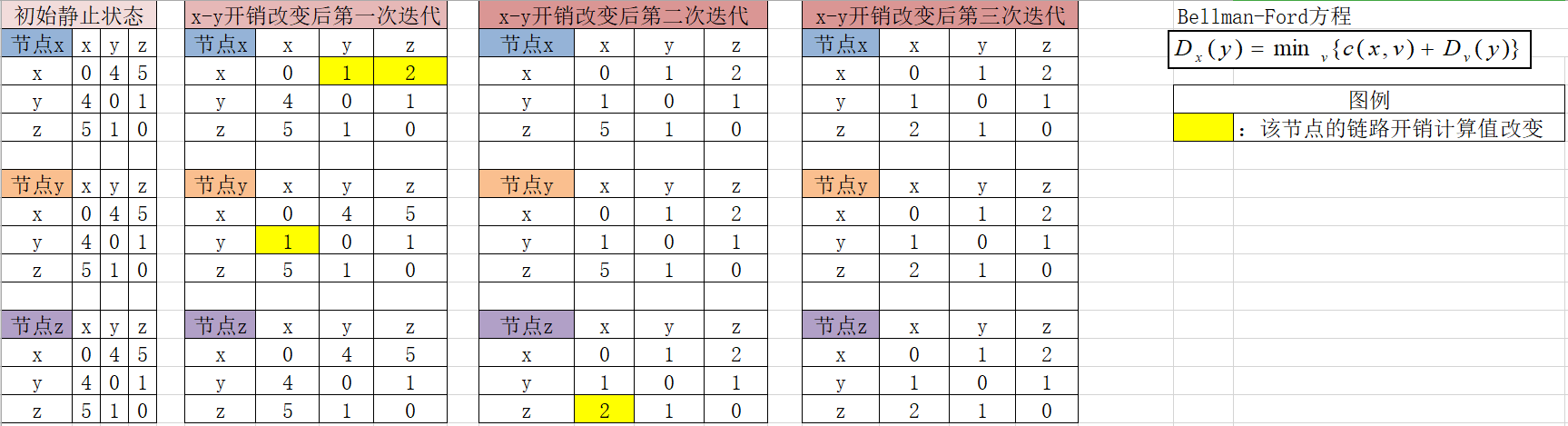
- 由此可以看出,对于链路开销减少的好消息,所有节点仅用三次迭代就完成了所有节点的链路开销更新。
- 节点链路开销表变化如下
- 链路开销增加实例
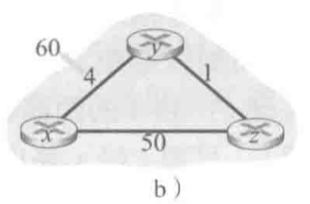
- 节点链路开销表变化如下
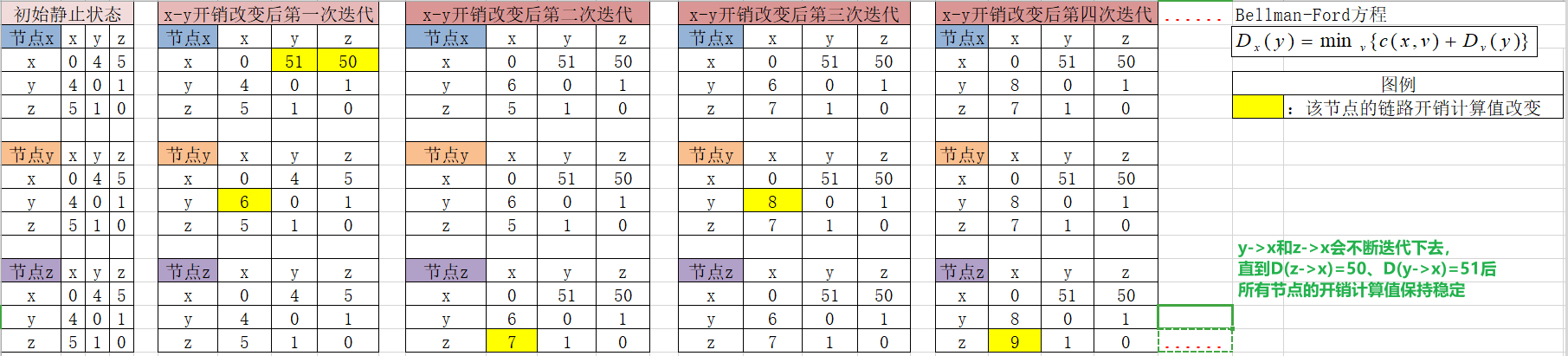
- 由此可以看出,关于链路开销增加的坏消息,所有节点需要用较多的迭代次数才能完成所有节点的链路开销更新,若$c(y,x)$由4便为10000且$c(z,x)$为9999,那么各节点的迭代次数将会非常多,因此,该问题称为count-to-infinity无穷计数问题。要想解决解决该问题,我们可以使用一种名为“posioned reverse毒性逆转”的计数加以避免。
- 节点链路开销表变化如下
3.2.2 posioned reverse毒性逆转
- 基本思想
- 若节点z通过节点y路由选择到目的节点x,则节点z将通告节点y,节点z到节点x的链路开销时∞,即$D_z(x)=∞$。只要节点z经过节点y路由选择到节点x,则节点z就持续地向节点y通告这条信息(谎言)。而因为节点y相信节点z没有到节点x的路径,即在节点y的表项中,$D_z(x)=∞$,因此节点y将永远不会示图经过节点z路由选择到节点x。
- 解决问题实例(结合3.2.1 链路开销增加实例产生的无穷计数问题)
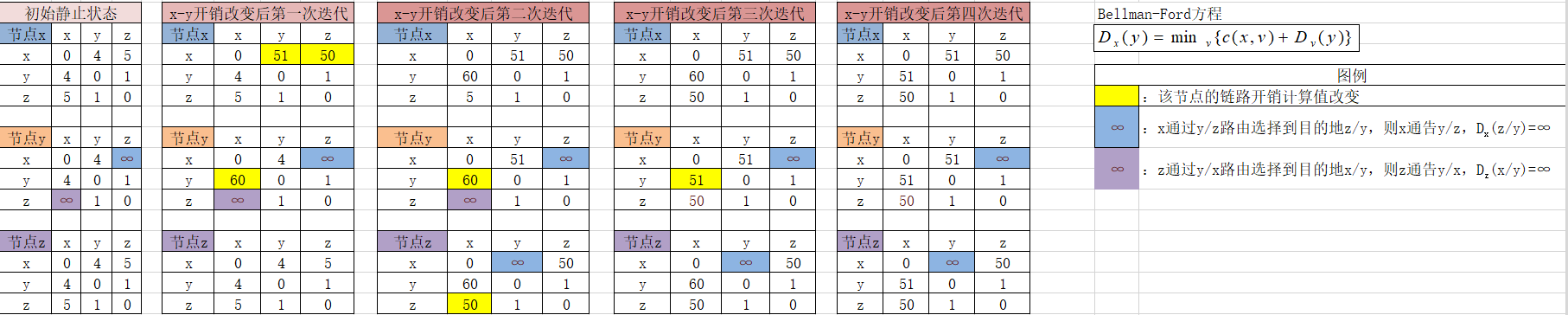
- 需要注意,poisoned reverse方法无法解决一般性的无穷计数问题,即当网络中节点存在涉及3个或更多节点的环路时将无法使用毒性逆转计数解决。
四、LS与DV路由算法的比较
- 报文复杂性
- LS算法
- LS算法要求每个节点均知晓网络中每条链路的开销,因此要求发送$O(|N||E|)$个报文,且无论何时有一条链路的开销发生改变,必须向所有节点发送新的链路开销。
- DV算法
- DV算法要求在每次迭代时,各节点在直接相连的邻居之间交换报文。当某条链路开销改变时,DV算法仅要求该节点在“新的链路开销导致该节点的某条最低开销链路的开销”发生改变时,该节点才传播已改变的链路开销。
- LS算法
- 收敛速度
- LS算法
- $O(|N|^2)$
- DV算法
- DV算法收敛较慢,且在收敛过程中可能会遇见路由选择环路、无穷计数问题。
- LS算法
- 健壮性
- LS算法
- 每个LS节点仅计算自己的转发表,因此在LS算法中,路由计算在某种程度上是分离的,这提供了一定程度的健壮性。
- DV算法
- DV算法中,每个节点可能会想邻居节点通告不正确信息,即各节点之间的耦合性较强,因此健壮性较弱。
- LS算法
- 综上,LS与DV算法没有明显的赢家,双方在因特网中均有应用。
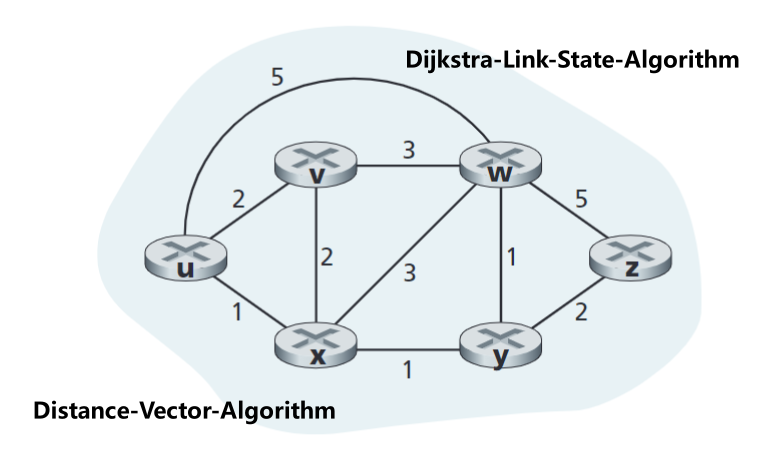 本文重点介绍Dijkstra算法及Distance-Vector(DV)算法原理。
本文重点介绍Dijkstra算法及Distance-Vector(DV)算法原理。