【CodeForces训练记录】CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)

训练情况

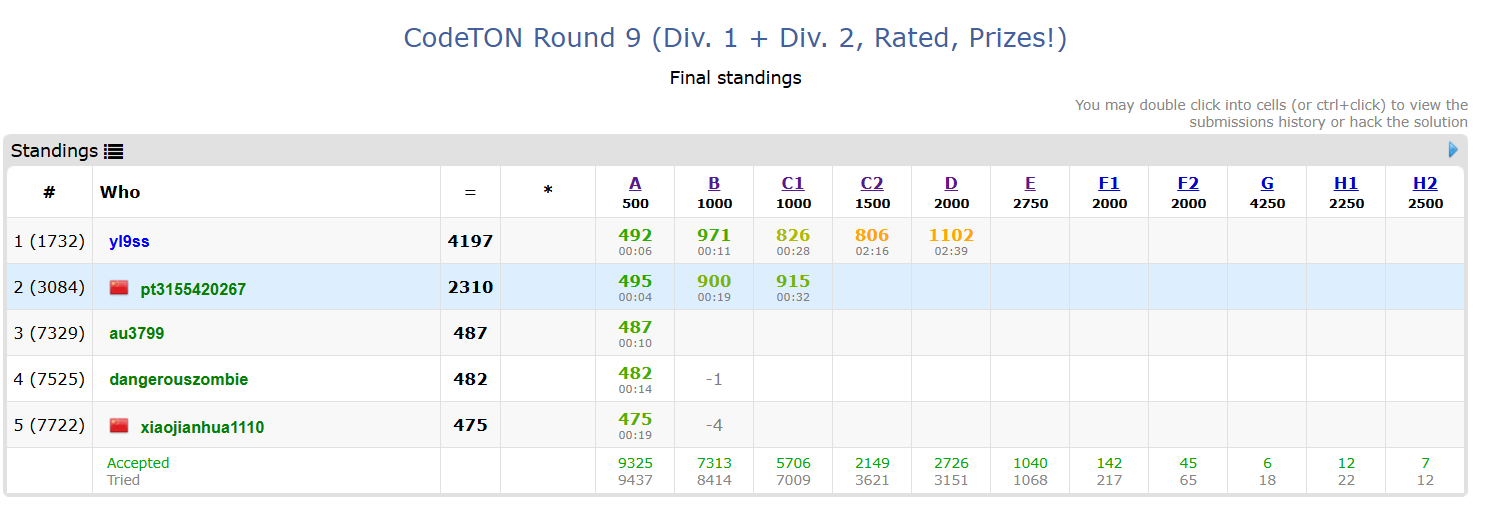
赛后反思

发现自己越来越能猜结论了，连续两题结论猜对了，一把rating上青了。

A题

构造一个数组使得模数互不相同，考虑构造一个模数为 \([0,1,2,3,4,5]\) 的数列，所以一个全是奇数的数列 \([1,3,5,7,9]\) 符合条件，直接输出 \(1 \sim n\) 的奇数即可。

#include <bits/stdc++.h>
// #define int long long
#define endl '\n'using namespace std;void solve(){int n; cin>>n;vector<int> cnt(103,0);int j = 1;for(int i = 0;i<n;i++){for(;j<=100;j++){if(j%(i+1)==i&&!cnt[j]){cnt[j]++;cout<<j<<" ";break;}}}cout<<endl;
}signed main(){int T; cin>>T; while(T--)solve();return 0;
}

B题

定义函数 \(f(s)\) 为字符串 \(s\) 的非空子串，非空子串的个数要为偶数，考虑较小的情况，连续的两个相同 \(f(s)\) 为偶数，例如 \(f(aa) = a + aa = 2\)，或者连续三个互不相同，例如 \(f(abc) = a + b + c + ab + bc + abc = 6\)，所以我们只要判断字符串中是否有连续两个相同，或者连续三个互不相同即可。

#include <bits/stdc++.h>
// #define int long long
#define endl '\n'using namespace std;void solve(){string s; cin>>s;int n = s.size();for(int i = 0;i<n-2;i++){string t = s.substr(i,3);bool flag = true;for(int j = 0;j<3;j++){for(int k = j+1;k<3;k++){if(t[j] == t[k]) flag = false;}}if(flag){cout<<t<<endl;return;}}for(int i = 0;i<n-1;i++){string t = s.substr(i,2);bool flag = t[0]==t[1];if(flag){cout<<t<<endl;return;}}cout<<-1<<endl;
}signed main(){int T; cin>>T; while(T--)solve();return 0;
}

C题

使得 xor（异或） 后能被 \(x,y\) 整除，首先 \(a \mod b\) 时，如果 \(b>a\) 那么模数一定不为零，所以如果 xor 后把 \(x\) 最高位的更高位变成 \(1\)，那么之后的模数一定不为零，所以这题枚举的上界就为 \(min(2x,m)\)。

#include <bits/stdc++.h>
#define int long long
#define endl '\n'using namespace std;void solve(){int x,m; cin>>x>>m;int ans = 0;for(int i = 1;i<=min(m,x*2);i++){if(x == i) continue;if(x%(x^i) == 0 || i%(x^i) == 0){ans++;// cout<<i<<endl;}}cout<<ans<<endl;// cout<<endl;
}signed main(){int T; cin>>T; while(T--)solve();return 0;
}