感觉今天脑子特别不清醒AWA
A.Strange Table
CF原题链接
题目大意:
给出两种矩阵的排列方式:
- 竖排
- 横排
每次给出\(n,m,k\),求在\(n\times m\)的矩阵中,对于竖排数字为\(k\)的位置,横排数字是多少\((1\leqslant n,m\leqslant 10^{6},1\leqslant k\leqslant n\times m)\)
解题思路:
直接做做完了。通过一些加减乘除求出数字\(k\)在竖排中的位置坐标\((x,y)\),再通过一些加减乘除求出横排中\((x,y)\)的数即可。
可恶啊,刚开始取模的时候没特判0
小代码
#incIude <bits/stdc++.h>
#define int long long
using namespace std;
int T;
int n,m,x;
signed main()
{scanf("%lld",&T);while (T--){scanf("%lld%lld%lld",&n,&m,&x);int r=x%n,c=(x+n-1)/n;if (r==0) r=n;printf("%lld\n",(r-1)*m+c);}return 0;
}
B.Partial Replacement
CF原题链接
题目大意:
给出一个由' . '和' * '组成的字符串\(s\),每次操作需要将一个' * '改为' x ',使得对于所有\(s_{i}=s_{j}=' x\ '\),满足\(j-i\leqslant k\)
特别地,要求第一个与最后一个' * '必须变为' x '。
求使字符串满足条件时,最少的操作次数。保证给出数据有合法解。\((1\leqslant k\leqslant n\leqslant 500)\)
解题思路:
直接模拟做做完了。用\(pre\)记录上一个变为' x '的位置,用\(lst\)记录上一个' * '的位置,若当前\(i-pre>k\),那么\(lst\)就一定要变成' x '。注意特判第一个和最后一个,额外\(+1\)的时候不要重复加。
小代码
#incIude <bits/stdc++.h>
#define int long long
using namespace std;
int T;
int n,k;
string str;
int cnt,tol;signed main()
{cin>>T;while (T--){cin>>n>>k>>str;cnt=tol=0;int _size=str.size();int pre=-1,lst=0;for (int i=0;i<_size;i++){if (str[i]!='*') continue;if (pre==-1) lst=i;if (i-pre>k||pre==-1) cnt++,pre=lst;lst=i,tol++;}if (tol>1) cnt++;printf("%lld\n",cnt);}return 0;
}
C.Double-ended Strings
CF原题链接
题目大意:
给出两个字符串\(a,b\),每次操作可以删去一个字符串的第一个字符或最后一个字符,求至少需要多少次操作可以使得\(a,b\)完全相同。\((1\leqslant |a|,|b|\leqslant 20)\)
解题思路:
逆转题意,我们可以将题意转化为:求\(a,b\)的最长公共子串长度\(len\),输出\(|a|+|b|-len\times 2\)。注意到极小的数据量,我们可以直接设状态\(f_{i,j}\)表示以\(a_{i},b_{j}\)结尾的最长公共子串的长度,状态转移方程也很好想,就是
小代码
#incIude <bits/stdc++.h>
#define int long long
using namespace std;
const int N=25;
int T;
string a,b;
int f[N][N];
int ans;signed main()
{cin>>T;while (T--){cin>>a>>b;int size1=a.size(),size2=b.size();a=" "+a,b=" "+b;ans=0;for (int i=1;i<=size1;i++){for (int j=1;j<=size2;j++){if (a[i]==b[j]) f[i][j]=f[i-1][j-1]+1;else f[i][j]=0;ans=max(ans,f[i][j]);}}cout<<size1+size2-ans*2<<'\n';}return 0;
}
D.Epic Transformation
CF原题链接
题目大意:
给出一个长度为\(n\)的序列\(a\),每次操作可以选择\(i,j\) 满足\(a_{i}\neq a_{j}\)并删除\(a_{i},a_{j}\),求序列\(a\)经过若干次操作后最少有多少个数。\((1\leqslant \Sigma n\leqslant 2\times 10^{5},1\leqslant a_{i}\leqslant 10^{9})\)
解题思路:
注意到什么情况下会剩下数。设\(k\)为序列中值为某数的个数,只要\(k\leqslant \lfloor\frac{n}{2}\rfloor\)那么一定有法两两匹配;但若是存在\(k>\lfloor \frac{n}{2}\rfloor\),那么一定会剩下 \(k\times2-n\) 个数无法匹配。显然,这样的数在整个序列中最多只会存在一个,所以统计最大的\(k\)值即可。再次注意到\(a_{i}\)的值域,再次用\(map\)当桶数组。
注意到两两匹配,那么还需要判断一下\(n\)的奇偶再输出。
小代码
#incIude <bits/stdc++.h>
#define int long long
using namespace std;
const int N=2e5+5;
int T;
int n,a[N];
map <int,int> bx;
int k;signed main()
{scanf("%lld",&T);while (T--){k=0;bx.clear();scanf("%lld",&n);for (int i=1;i<=n;i++){scanf("%lld",&a[i]);bx[a[i]]++;k=max(k,bx[a[i]]);}if (k<=n/2) printf("%lld\n",n%2);else printf("%lld\n",k*2-n);}return 0;
}
E.Restoring the Permutation
CF原题链接
题目大意:
给出一个长度为\(n\)的序列\(q\),要求分别输出字典序最小、字典序最大的合法排列\(p\)。我们认为排列\(p\)合法,当且仅当:
- \(p\)是长度为\(n\)的排列
- 对于\(\forall i\in [1,n]\),有\(q_{i}=max\{p_{1},p_{2},…,p_{i}\}\)
\((1\leqslant n\leqslant 2\times 10^{5},1\leqslant q_{i}\leqslant n)\)
解题思路:
翻译题意后,原题相当于:给出一个排列的前缀最大值数组\(q\),要求输出字典序最大、最小的原排列\(p\)。
直接模拟做完了。用\(set\)维护剩下可选的数,若\(q_{i}\neq q_{i-1}\),那么一定满足\(p_{i}=q_{i}\);若\(q_{i}=q_{i-1}\),那么贪心考虑\(p_{i}\)即可。
小代码
#incIude <bits/stdc++.h>
#define int long long
using namespace std;
const int N=2e5+5;
int T;
int n,q[N];
int ans1[N],ans2[N];
set <int> st1,st2;signed main()
{scanf("%lld",&T);while (T--){scanf("%lld",&n);for (int i=1;i<=n;i++) scanf("%lld",&q[i]);for (int i=1;i<=n;i++) st1.insert(i),st2.insert(i);for (int i=1;i<=n;i++){if (q[i]!=q[i-1]) {ans1[i]=ans2[i]=q[i];st1.erase(q[i]),st2.erase(q[i]);continue;}set <int> ::iterator it=st2.lower_bound(q[i]);it--;ans2[i]=*it;st2.erase(*it);set <int> ::iterator it2=st1.begin();ans1[i]=*it2;st1.erase(*it2);}for (int i=1;i<=n;i++) printf("%lld ",ans1[i]);printf("\n");for (int i=1;i<=n;i++) printf("%lld ",ans2[i]);printf("\n");}return 0;
}
F.Triangular Paths
CF原题链接
题目大意:
考虑一个多层三角形,第\(k\)层有\(k\)个节点,层数从\(1\)开始标号。对于节点\((r,c)\),它分别有一条连向\((r+1,c),(r+1,c+1)\)的边。若\(r+c\)是偶数,那么到\((r+1,c)\)的边是有效边,否则到\((r+1,c+1)\)的边有效。
一开始在位置\((1,1)\),每次操作可以通过有效边到达下一层,或耗费1的代价,使得对于节点\((r,c)\),原本有效边变无效、原本无效边变有效。
现在给出\(n\)个点的标号\((r_{i},c_{i})\),要求输出可以全部经过这些点的最小大家。\((1\leqslant \Sigma n\leqslant 2\times 10^{5},1\leqslant c_{i}\leqslant r_{i}\leqslant 10^{9})\)
解题思路(口胡):
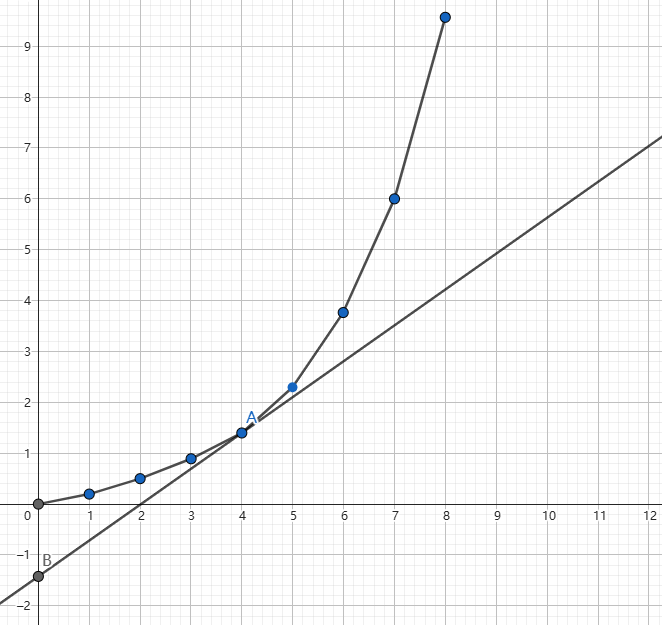
原题的图不助于理解题意,于是有了下图。

容易发现,原本的图形成了若干个不相交的子图,而同一个子图中\(\lfloor \frac{r-c}{2}\rfloor\)相等。在一个子图中,在左边的节点可以直接走到,在右边的需要代价,那么分类讨论一下。
若点\((r,c)\)满足\(r+c\mod 2=0\),那么这个点一定需要一定代价才能走到,统计需要新建的边即可。
若点\((r,c)\)满足\(r+c\mod 2=1\),那么它通过一些新建的边到达它所在的子图即可,统计它所在子图所需的代价即可。





![[EULAR2023]CLASSIC研究未达终点](https://img2024.cnblogs.com/blog/779861/202411/779861-20241124153844085-355998340.png)