强连通分量,缩点算法:Tarjan
代码及模板
强连通图:有向图,任意两点有路径
强连通分量:有向图,强连通子图数量
前置知识:dfs树(dfs序构成的树)
成分:
1.树边:dfs树上的边
(以下三种边是dfs树上没有但原图上有的边)
2.前向边:dfs树的祖先到儿子的边。
3.返祖边(后向边):儿子到祖先的边
4.横向边:旁系亲戚的边(没有直接的祖父关系,可能是兄弟节点之类的)
性质:返祖边和横向边的dfn(dfs序)u < v (不然被直接更新成树边)且因为是dfs,所以v已经判断完了。
所以可以每次遇到一条dfn[u] < dfn[v] 的边,都可以更新low[u] = min(low[u], low[v])
每次递归搜索的时候,都要更新low[u] = min(low[u], low[v])子节点有可能找到了返祖边,那么父节点的low也是儿子的low
循环结束后,如果low[u] = dfn[u],说明u是环的根,栈后面的元素都属于该强联通图,染色,出栈。
具体的代码实现有点有趣。
#include <stack>int dfn[MAXN], tot = 0;
bool instack[MAXN];
int low[MAXN];
int co[MAXN], col = 0;
std::stack<int> stk;void Tarjan(int u)
{dfn[u] = ++tot;low[u] = dfn[u]; // 一开始low[u]是自己,有后向边再更新stk.push(u);instack[u] = true;for(int e = first[u]; e; e = nxt[e]){int v = go[e];if(!dfn[v]){Tarjan(v);low[u] = min(low[u], low[v]); // 子节点更新了,我也要更新// 若子节点没更新,则min能够保证low[u] == dfn[u]}else if(instack[v]) // v访问过且在栈中,意味着u→v是后向边{low[u] = min(low[u], dfn[v]);}}if(low[u] == dfn[u]) // 是SCC中的第一个被访问的节点{co[u] = ++col;while(stk.top() != u) co[stk.top()] = col, instack[stk.top()] = false, stk.pop();// 染色,弹栈instack[u] = false;stk.pop(); // 最后把u弹出去}
}
缩点
即把同一强连通分量的点变成一个点,新点权为scc里所有点权之和
割点
定义:删了该点图不连通的点叫割点
换句话说:若x是割点,则存在 y∈T(x) 满足y不经过 x 能到达的所有点均属于 T(x)。(注:T(x)表示x的dfs子树)
所有的儿子节点的low小于\(dfn_u\)
使得$ low_v \geq dfn_u $,即不能回到祖先,那么 u 点为割点。
割边(桥)
当枚举到边u-v时,若low_v > low_u时,该边为桥。
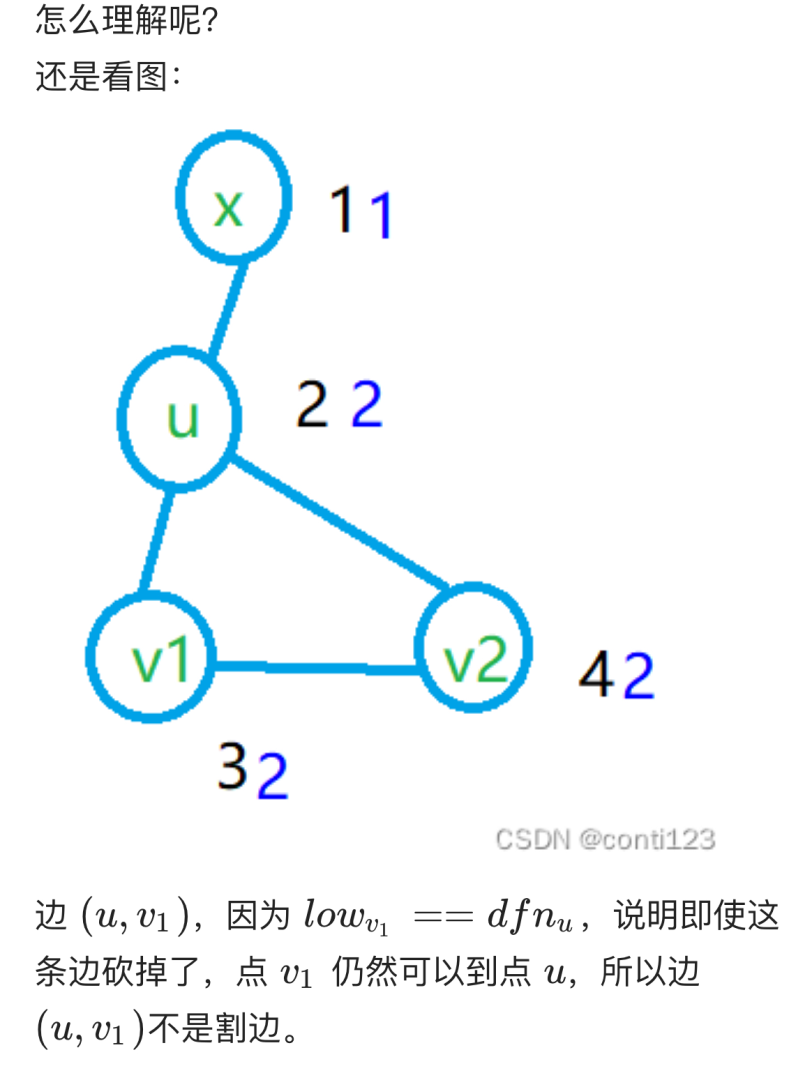
边,点双连通分量
定义:
在一张连通的无向图中,对于两个点 u 和 v,如果无论删去哪条边(只能删去一条)都不能使它们不连通,我们就说 u 和 v 边双连通。
在一张连通的无向图中,对于两个点 u 和 v,如果无论删去哪个点(只能删去一个,且不能删 u 和 v 自己)都不能使它们不连通,我们就说 u 和 v 点双连通。
边双连通具有传递性, 而点双连通不具有传递性
一个边/点双连通分量 == 边/点双连通子图
边双连通分量求法:
在 DFS 生成树上的一个强连通分量,在原无向图中是边双连通分量。可以发现,求边双连通分量的过程实际上就是求强连通分量的过程。
最后记得判重边****
桥(割边)的求法
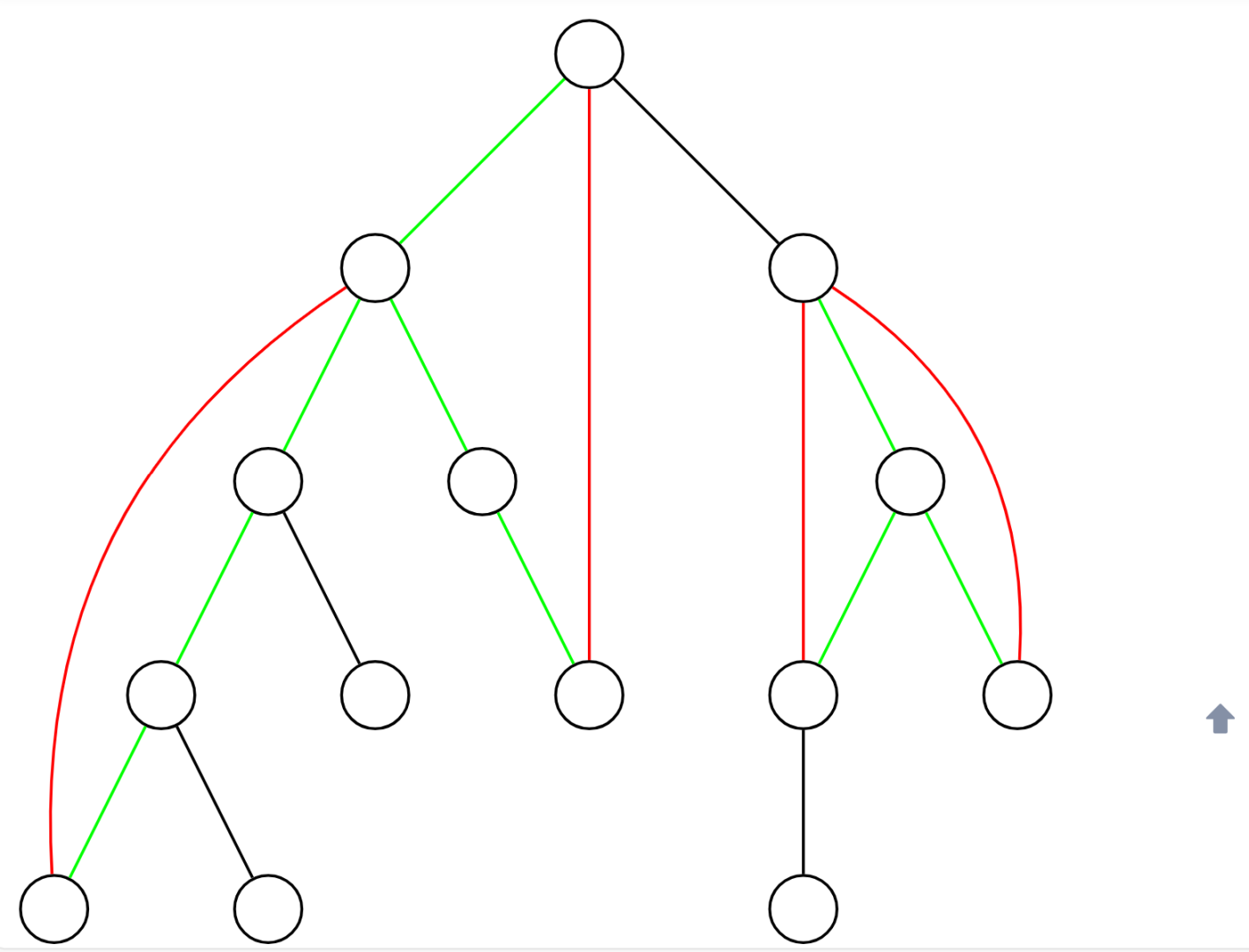
如上图所示,黑色与绿色边为树边,红色边为非树边。每一条非树边的两个端点都唯一对应了树上的一条由树边构成的简单路径,我们说这条非树边 覆盖 了这条简单路径上所有的边。
在图中,绿色的树边 至少 被一条非树边覆盖,黑色的树边不被 任何 非树边覆盖。
显然,非树边 和 绿色的树边 一定不是桥,黑色的树边 一定是桥。
首先考虑一个暴力的做法,对于每一条非树边,都逐个地将它覆盖的每一条树边置成绿色,时间复杂度为 O(nm)。
考虑用差分优化。对于每一条非树边,在其树上深度较小的端点处打上 -1 标记,在其树上深度较大的端点处打上 +1 标记,然后 O(n) 求出每个点的子树内部的标记和。
对于一个点 u,其子树内部的标记之和等于覆盖了 u 和 fa_u 之间的树边的非树边数量。若这个值等于 0,则 u 和 fa_u 之间的树边是 桥。
void TJ(int u, int fa){dfn[u] = ++cnt, low[u] = dfn[u]; sta.push(u);for(auto v : edge[u]) if(v != fa)/*防止回环*/{if(!dfn[v]) TJ(v, u);low[u] = min(low[u], low[v]);}if(dfn[u] == low[u]){//??? co[++col].push_back(u);while(sta.top() != u) {int x = sta.top();scc[x] = col;co[col].push_back(x), sta.pop();}scc[u] = col;sta.pop();}
}//我自创的优美边双写法
点双的求法 模板
题解 (个人感觉题解写得就很好)
oi-wiki
可能有且只有割点可能同时存在两个点双图中。
每遇到一个割点(见割点的求解方法),就弹出一些点放到一个点双中。
void TJ(int u, int rt) {dfn[u] = low[u] = ++ tot;if(u == rt && !edge[u].size()) //孤立点的特判 scc[++ col].push_back(u);stk[++ tp] = u;for(auto v : edge[u]) {if(!dfn[v]) {TJ(v, rt);low[u] = min(low[u], low[v]);if(low[v] >= dfn[u]) {//点u一定为割点 scc[++ col].push_back(u);while(stk[tp] != v) {//割点点u不会被弹出 scc[col].push_back(stk[tp]);-- tp;} scc[col].push_back(stk[tp]);-- tp; //注意到 if(low[v] >= dfn[u])是在TJ(v)后的,所以实际执行时间比较晚 //故弹栈中元素最多只能弹到v,剩下的元素要让之前的某个u(dfn更小的节点)来弹出 }}else low[u] = min(low[u], dfn[v]);//}
}