前言
这篇博客主要用于记录一些关于电机一些专有名词分析的事情,特此记录,一方面便于日后自己的温故学习,另一方面也比便于大家的学习和交流。如有不对之处,欢迎评论区指出错误,你我共同进步学习!
这里摘要自b站的这位老师的视频,原视频很长,这里做出一定程度的总结:
点击跳转至原视频
正文
一、力矩
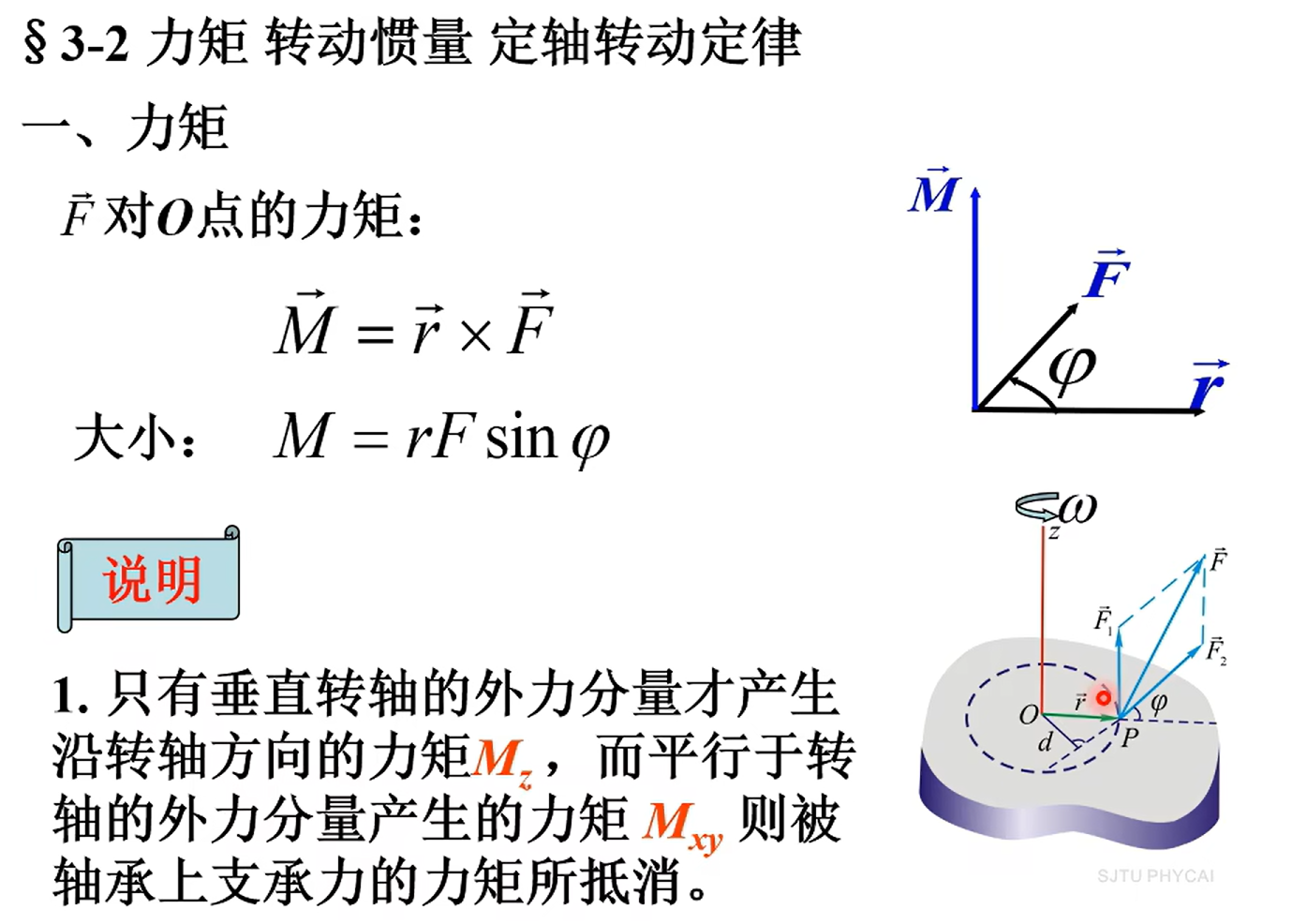
二、角速度和线速度

角速度,指的是单位时间内转过的角度值
线速度,指的是单位时间内转过的距离值
角加速度,指的是单位时间内,角速度的增加值
线加速度,指的是单位时间内,线加速度的增加值
转速,可以指的是一分钟转多少圈r/min,也可以是r/s
三、转动惯量
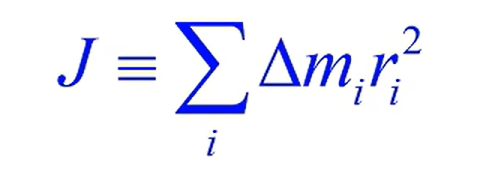
刚体对于转轴的转动惯量,刚体在受到外力力矩作用下能够保持原来运动状态的惯性量度的大小。
【单位】 \(kg * m^2\)

【转动惯量的先决条件】是关于哪个转轴来说的。。
我自己的直观理解是,这个变量除了可以类比质量m外,利用牛一(惯性定理去理解),也可以认为是一种保持的变量。就是转动惯量大的话,一般惯性越大,就像载满货物的火车不好刹车,因为它惯性大,同样,转动惯量大的电机一旦转起来也就不好停下来。
那我自己的机器人举一个简单的例子,一开始我给关节电机的转动惯量很小,就导致受到一点点的力就可以把机器人整体拉飞起来(懂我意思吧,电机不好保持原来的状态了),就很塑性。
四、刚体定轴转定定律

其实这里可以和牛顿第二定律进行类比,方便进行理解

五、电机的扭矩
先说计算公式:
\(P = \frac{(F\times S)}{t}\)
F是做功的力,S是距离,t是时间
因为距离除以时间等于速度,所以功率又可以用来表示为:
\(P = F \times v\)
我们又引入了转速n,单位是rpm,表示每分钟转多少圈: \(n = \frac{Revolutions}{Per Minute}\)。
同时我们又知道线速度: \(v = n \times 2 \pi R\) ,表示每分钟电机转动的距离,类比于速度,一秒钟走过的距离。其中R为半径.
带入上式可以得到功率的表达式:
\(P = F\times n \times 2 \pi R\)
又因为电机产生的扭矩为:
\(M = F \times R\)
所以综合上述得到电机的扭矩公式为:
\(M = F \times R = \frac{P}{n \times 2 \pi R} \times R = \frac{P}{2\pi n}\)
通常习惯上用每分钟转过圈数表示,就是英语中的Revolutions Per minute(rpm),没有单位;
电机功率通常用千瓦表示;
扭矩用牛顿每米表示,即牛米。
统一单位后公式变为:
\(M = \frac{1000P}{\frac{n}{60}\times 2\times \pi}\)
整理以下常数部分:
\(\frac{1000 \times 60}{2\pi} \approx 9549.296748407161\)
大致取常数9550
所以最后就得到了扭矩和转速的公式:
\(M = \frac{9550\times P}{n}\)
P的单位是Kw
n的单位是rpm
可以看到,在功率一定的情况下,电机扭矩和转速是成反比的,当电机转速越大,扭矩越小;当电机扭矩越大,则电机转速越小。