pencil
挺板的,点\(u\)的答案是\(dis(1,u)+dis(u,n)\),边\(e=(u,v)\)的答案是\(\min(dis(1,u)+dis(v,n),dis(1,v)+dis(u,n))+w(e)\)。其中\(dis(u,v)\)表示\(u\)到\(v\)的最短路。
从\(1\)和\(n\)各跑一次Dijkstra,预处理出到\(1\)和到\(n\)的最短路即可。
点击查看代码
#include<bits/stdc++.h>
#define PII pair<int,int>
#define int long long
#define N 100010
#define M 200010
using namespace std;
struct edge{int to,w;};
vector<edge> G[N];
int n,m,d[N],d2[N],uu[M],vv[M],ww[M];
priority_queue<PII,vector<PII>,greater<PII>> q;
void dijkstra(vector<edge> G[],int d[N],int s){memset(d,0x3f,N*sizeof(int));d[s]=0,q.push({0,s});while(!q.empty()){auto t=q.top();q.pop();int u=t.second,dis=t.first;if(dis>d[u]) continue;for(auto i:G[u])if(dis+i.w<d[i.to])d[i.to]=dis+i.w,q.push({d[i.to],i.to});}
}
signed main(){ios::sync_with_stdio(false);cin.tie(nullptr),cout.tie(nullptr);cin>>n>>m;for(int i=1;i<=m;i++){cin>>uu[i]>>vv[i]>>ww[i];G[uu[i]].emplace_back((edge){vv[i],ww[i]});G[vv[i]].emplace_back((edge){uu[i],ww[i]});}dijkstra(G,d,1),dijkstra(G,d2,n);for(int i=1;i<=n;i++) cout<<d[i]+d2[i]<<"\n";for(int i=1;i<=m;i++)cout<<min(d[uu[i]]+d2[vv[i]],d[vv[i]]+d2[uu[i]])+ww[i]<<"\n";return 0;
}
arrangement
题面勘误:要计算的是\(q\)的个数,而非\(p\)。
原问题显然可以反过来考虑\(p\)转成\(s\)。
由于\(q\)是一个排列,所以每相邻两个数必须恰好交换\(1\)次。也就是说,如果在\(k\)处完成了交换,\(p[1,k]\)和\(p[k+1,n]\)就是相互独立的了,只能内部交换。
所以我们考虑区间DP。设\(f[i][j]\)表示\(p[i,j]\)转成\(s[i,j]\)的情况数。对于区间\([i,j]\),它可以分割为\(p[1,k]\)和\(p[k+1,n]\)来计算贡献,当且仅当下面的条件全部成立:
- \(k\in [i,j)\)。
- \(p[l,k]\)恰好包含\([l,k-1]\)以及\(k+1\)。
- \(p[k+1,r]\)恰好包含\(k\)以及\([k+2,r]\)。
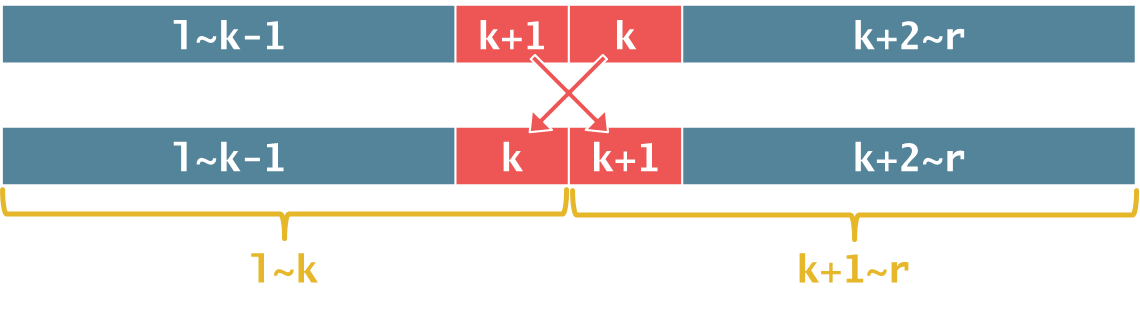
理解:因为交换\(k\)与\(k+1\)后,\(p[l,k]\)和\(p[k+1,r]\)就独立了,所以为了使得最终\(p[i]=s[i]=i\),必须抓住此次交换的机会,使得\(p[l,k]\le k,p[k+1,r]>k\)。
对于满足条件的\(k\),有转移\(f[i][j]=\sum\limits_{k}(f[i][k]\times f[k+1][j]\times C_{j-i-1}^{k-i})\)。
转移方程也比较好理解,因为左右独立所以顺序可以随意选择。除去\(k\)的交换,左右区间一共交换\(j-i-1\)次,从这个区间中选取哪些交换属于右区间,就得到\(C_{j-i-1}^{k-i}\)了。
代码实现中,check()函数用于检查\(k\)是否满足转移的条件。
总时间复杂度应该是\(O(n^4\log n)\),其中:
- 转移复杂度是\(O(n^2\log n)\),其中\(O(n)\)枚举\(k\),\(O(n\log n)\)排序。
- 枚举状态是\(O(n^2)\)。
点击查看代码
#include<bits/stdc++.h>
#define int long long
#define mod 1000000007
#define N 52
using namespace std;
int n,p[N],f[N][N],C[N][N],tmp[N];
bitset<N> bi;
bool check(int l,int r,int k){memcpy(tmp+l,p+l,(r-l+1)*sizeof(int));for(int i=l;i<=k;i++) bi[p[i]]=0;for(int i=k+1;i<=r;i++) bi[p[i]]=1;sort(tmp+l,tmp+r+1);swap(tmp[k],tmp[k+1]);for(int i=l;i<=k;i++) if(bi[tmp[i]]) return 0;for(int i=k+1;i<=r;i++) if(bi[tmp[i]]^1) return 0;return 1;
}
signed main(){cin>>n;for(int i=1;i<=n;i++) cin>>p[i];C[0][0]=1;for(int i=1;i<=n;i++){C[i][0]=1;for(int j=1;j<=i;j++){C[i][j]=(C[i-1][j]+C[i-1][j-1])%mod;}}for(int i=1;i<=n;i++) f[i][i]=1;for(int len=2;len<=n;len++){for(int i=1;i+len-1<=n;i++){int j=i+len-1;for(int k=i;k<j;k++){if(!check(i,j,k)) continue;f[i][j]=(f[i][j]+f[i][k]*f[k+1][j]%mod*C[j-i-1][k-i]%mod)%mod;}}}cout<<f[1][n]<<"\n";return 0;
}
似乎网上有\(O(n^2)\)的做法?这几天补出来。
divide
题面勘误:“计算最终的\(b-a\)”\(\Longrightarrow\)“计算最终的\(a-b\)”。
看似博弈,实则DP。
首先我们对\(a\)进行排序(同时去重也可以,因为相同大小的糖果最多选\(1\)堆)。
我们把整局的先手称为A,后手称为B。
我们定义:
- \(f[i]\)表示第\(i\)堆被A选择后,\(i\sim n\)的总答案。
- \(g[i]\)表示第\(i\)堆被B选择后,\(i\sim n\)的总答案。
A的选择对答案\(a-b\)的贡献为正,B则为负。
有转移:
-
当\(i\)之后存在\(j\)满足\(j\in(i,n],a[j]-a[i]\le k\),那么对于所有的\(j\),有转移:
- \(f[i]=\min(g[j])+a[i]\);
- \(g[i]=\max(f[j])-a[i]\)
这是因为一个人完成操作后,足够聪明的另一个人会选择对ta最优的操作,因此这里我们需要考虑最坏的情况。最后累加\(a[i]\)的贡献。
-
当不存在这样的\(j\)时,\(f[i]=a[i],g[i]=-a[i]\),因为\(a[i]\)无论被谁选择,游戏都结束了,所以不再累加其他贡献。
点击查看代码
#include<bits/stdc++.h>
#define int long long
#define N 10010
using namespace std;
int n,k,a[N],g[N],f[N],ans=INT_MIN;
signed main(){ios::sync_with_stdio(false);cin.tie(nullptr);cin>>n>>k;for(int i=1;i<=n;i++) cin>>a[i];sort(a+1,a+1+n);for(int i=n;i>=1;i--){int maxx=INT_MIN,minn=INT_MAX;for(int j=i+1;j<=n;j++){if(a[j]-a[i]>k) break;maxx=max(maxx,f[j]);minn=min(minn,g[j]);}f[i]=(minn!=INT_MAX?minn+a[i]:a[i]);g[i]=(maxx!=INT_MIN?maxx-a[i]:-a[i]);}for(int i=1;i<=n;i++){if(a[i]>k) break;ans=max(ans,f[i]);}cout<<ans<<"\n";return 0;
}
然后我们发现\(f\)和\(g\)其实是对称的操作,\(f[i]\)和\(g[i]\)互为相反数。所以我们可以将\(g\)省去,然后用\(-maxx\)代替\(minn\)。
点击查看代码
#include<bits/stdc++.h>
#define int long long
#define N 10010
using namespace std;
int n,k,a[N],f[N],ans=INT_MIN;
signed main(){ios::sync_with_stdio(false);cin.tie(nullptr);cin>>n>>k;for(int i=1;i<=n;i++) cin>>a[i];sort(a+1,a+1+n),memset(f,-0x3f,sizeof f);for(int i=n;i>=1;i--){int maxx=INT_MIN;//minn=-maxxfor(int j=i+1;j<=n;j++){if(a[j]-a[i]>k) break;maxx=max(maxx,f[j]);}f[i]=(maxx!=INT_MIN?a[i]-maxx:a[i]);}for(int i=1;i<=n;i++){if(a[i]>k) break;ans=max(ans,f[i]);}cout<<ans<<"\n";return 0;
}
zerone
作为最后一道题,算比较无脑的了。
先考虑链的特殊性质。显然当且仅当“区间大小为偶数,且区间内\(1\)的个数为奇数”时,组不成回文串。我们可以用线段树来维护区间内\(1\)的个数。对于输出Yes的情况,我们为了让修改后的字典序最小,肯定得把\(1\)往中间靠,直接线段树区修即可。注意区间大小为奇数,\(1\)的个数为偶数时,最中间一位要空出来成为\(0\),时间复杂度\(O((n+q)\log n)\)。
至于树上的情况,套一个树剖即可解决。时间复杂度是\(O(n\log n+q\log^2 n)\)。
代码太长不太想写了,放个std。
点击查看代码
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cstdio>
#include<assert.h>
using namespace std;
char s[100005];
int a[100005],dep[100005],L,R,n,m,mjy;
int dfn[100005],siz[100005],big[100005],fa[100005],seq[100005],C,top[100005];
int x,y,tot,ver[200005],nxt[200005],head[100005];
int sum[2],c[2];
void add(int x,int y){ver[++tot]=y;nxt[tot]=head[x];head[x]=tot;ver[++tot]=x;nxt[tot]=head[y];head[y]=tot;
}
int cnt[2][500005],num[500005],flag[2][500005];
void update(int now){int lson=now<<1,rson=now<<1|1;cnt[0][now]=cnt[0][lson]+cnt[0][rson];cnt[1][now]=cnt[1][lson]+cnt[1][rson];
}
void pushdown(int now){int lson=now<<1,rson=now<<1|1;int op=flag[0][now] ? 0:1;if(flag[op][now]){flag[op][lson]=1;cnt[op][lson]=num[lson];flag[op^1][lson]=cnt[op^1][lson]=0;flag[op][rson]=1;cnt[op][rson]=num[rson];flag[op^1][rson]=cnt[op^1][rson]=0; }flag[op][now]=0;
}
void build(int now,int l,int r){if(l==r){cnt[a[seq[l]]][now]=1;cnt[a[seq[l]]^1][now]=0; num[now]=1;return;}int mid=(l+r)>>1;int lson=now<<1,rson=now<<1|1;build(lson,l,mid);build(rson,mid+1,r);update(now);num[now]=num[lson]+num[rson];
}
void check(int now,int l,int r){if(l>=L&&r<=R){sum[1]+=cnt[1][now];sum[0]+=cnt[0][now];return;}pushdown(now);int mid=(l+r)>>1;int lson=now<<1,rson=now<<1|1;if(L<=mid) check(lson,l,mid);if(R>mid) check(rson,mid+1,r);
}
void change(int now,int l,int r,int op){if(L>R) return;if(l>=L&&r<=R){flag[op][now]=1;cnt[op][now]=num[now];cnt[op^1][now]=flag[op^1][now]=0;return;}pushdown(now);int mid=(l+r)>>1;int lson=now<<1,rson=now<<1|1;if(L<=mid) change(lson,l,mid,op);if(R>mid) change(rson,mid+1,r,op);update(now);
}
void dfs1(int now,int an){fa[now]=an;siz[now]=1;big[now]=0;dep[now]=dep[an]+1;for(int i=head[now];i;i=nxt[i]){if(ver[i]!=an){dfs1(ver[i],now);siz[now]+=siz[ver[i]];if(big[now]==0||siz[ver[i]]>siz[big[now]])big[now]=ver[i];}}
}
void dfs2(int now,int TOP){top[now]=TOP;dfn[now]=++C;seq[C]=now;if(big[now]) dfs2(big[now],TOP);for(int i=head[now];i;i=nxt[i])if(ver[i]!=fa[now]&&ver[i]!=big[now])dfs2(ver[i],ver[i]);
}
int LCA1(int x,int y){sum[0]=0;sum[1]=0;while(top[x]!=top[y]){if(dep[top[x]]<dep[top[y]]) mjy=y,y=x,x=mjy;L=dfn[top[x]];R=dfn[x]; check(1,1,n);x=fa[top[x]];}if(dep[x]>dep[y]) mjy=y,y=x,x=mjy;L=dfn[x];R=dfn[y];check(1,1,n);if((sum[1]&1)&&(sum[0]&1)) return 0;else return dfn[x];
}
int work(int &x,int op,int lca){c[0]=sum[0]>>1,c[1]=sum[1]>>1;while(1){if(!c[op]) op^=1;if(!c[op]) return 0;R=dfn[x];L=dfn[top[x]];if(dep[top[x]]<dep[seq[lca]]) L=lca;if(R-L+1>c[op]) L=R-c[op]+1;change(1,1,n,op);c[op]=c[op]-(R-L+1);if(L==lca) return 1;if(L<=R) x=fa[seq[L]];}
}
void LCA2(int x,int lca){if(work(x,0,lca)) return;int op= (sum[1]&1) ? 1:0;if(sum[op]&1){L=R=dfn[x];change(1,1,n,op);x=fa[x];}work(x,1,lca);
}
int main(){ scanf("%d%d%s",&n,&m,s+1);for(int i=1;i<=n;i++)a[i]=s[i]-'0';for(int i=1;i<n;i++){scanf("%d%d",&x,&y);add(x,y);}dfs1(1,0);dfs2(1,1);build(1,1,n);int lca;for(int i=1;i<=m;i++){scanf("%d%d",&x,&y);if(lca=LCA1(x,y)){puts("Yes");LCA2(x,lca);LCA2(y,lca);}elseputs("No"); }return 0;
}