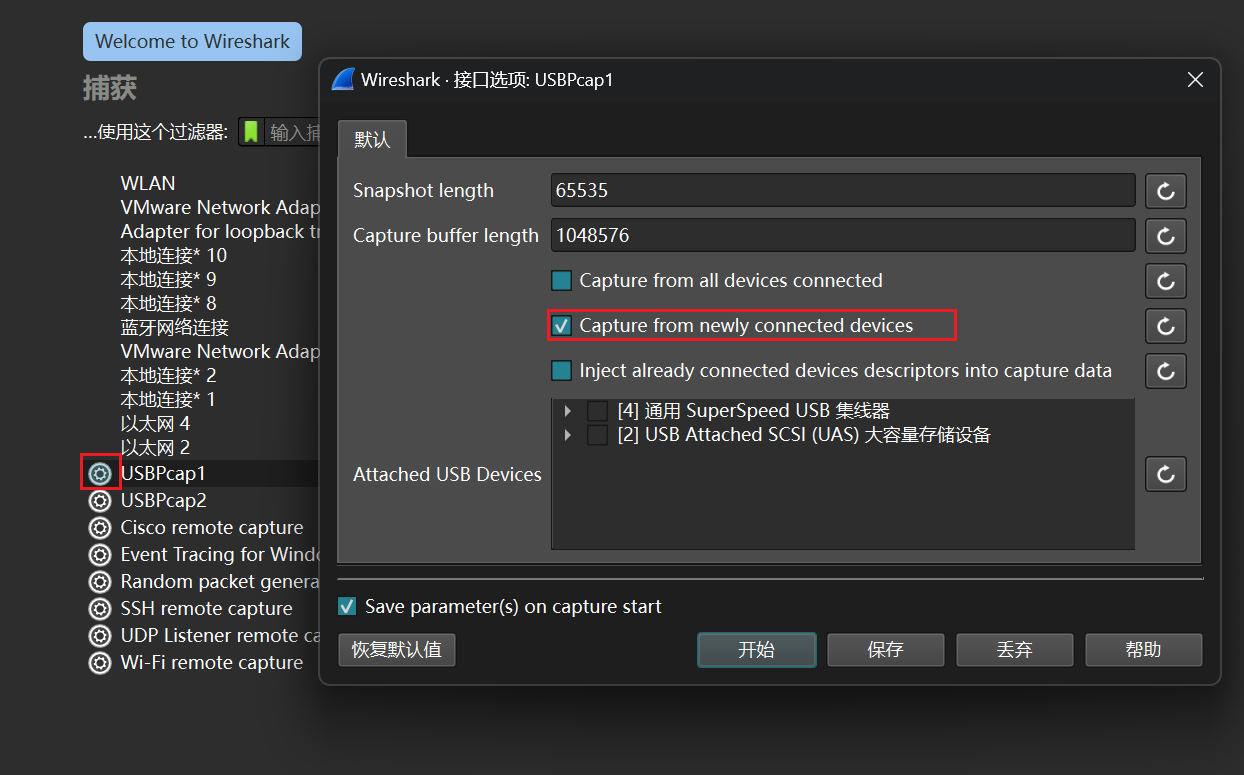
符号说明(部分)
存在唯一:\(\exist|\) 或 \(\exist!\)
使得:\(\operatorname{s.t.}\)(so that/such that)
非:\(\neg\)
正整数:\(\mathbb{Z}^+,\mathbb{N}_+,\mathbb{Z}_+,\mathbb{N}^+\)
定义为:\(\triangleq\) 或 \(\dot=\)
笛卡尔乘积
\(A\times B=\{(a,b)|a\in A,b\in B\}\)(\((a,b)\) 为有序对)
\(A\times B\times C=\{(a,b,c)|...\}\) VS \((A\times B)\times C=\{((a,b),c)|...\}\)
\(\mathbb{R}^2=\mathbb{R}\times \mathbb{R}\)
映射
仅讨论单值函数。
三要素:\((f,A,B)\)
\(A\):定义域。\(B\):值集。\(f(A)=\{f(x)\in B|x\in A\}\):值域。
一元实值函数:\((f,A)\)(\(B=\mathbb{R}\))。
未给出 \(A\),自然定义域,使得其有意义的所有实数(?)。
单射、满射、双射。
有限集、无限集
若 \(\exist n\in\mathbb{Z}^{+}\),s.t. \(A\) 与 \({1,2,3,\dots,n}\) 存在一个双射,则称 \(A\) 为有限集,且 \(\#A=n\)。
不是有限集的集合被称为无限集。
可列集
若 \(A\) 与 \(\mathbb{Z}^+\) 之间存在一个双射,则称 \(A\) 为可列集。
等势
证明 \((0,1)\) 不是可列集(康托对角线法,反证法):
假设 \((0,1)=\{r_n\}_{n=1}^{+\infin}\),
\(r_i=0.\overline{x_1^{(i)}x_2^{(i)}x_3^{(i)}\dots}\),其中 \(x_{i}^{(j)}\in\{0,1,\dots,9\}\)。
令 \(r=0.\overline{x_1x_2x_3\dots}\),满足 \(x_i\in\{1,2,\dots,8\}-\{x_i^{(i)}\}\),
则 \(r\in(0,1)\) 且 \(r\not\in \{r_n\}_{n=1}^{+\infin}\),矛盾。
故 \((0,1)\) 为不可数集。
数集与确界原理
约定:\(\empty\) 是有界集(有上界和下界)。
实数集
上确界
\(\sup S\)
定义:设 \(A\) 是一个 \(\R\) 的非空子集。
若 \(\exist \eta \in \R\),\(\texttt{s.t.}\):
-
\[\forall x\in A, x\le \eta \]
-
\[\forall(\alpha\in \R 且)\alpha < \eta,\exist x_0\in A, \texttt{s.t.}x_0 > \alpha \]
等价于:
\[\forall \epsilon \in \R 且 \epsilon>0,\exist x_0\in A,\texttt{s.t.} x_0>\eta-\epsilon \]
下确界
\(\inf S\)
定义:与上确界类似。
确界原理
非空有界(实)数集必存在确界。
例题:设 \(A=\{\frac{1}{n}|,n\in\Z^+\}\),证明:\(\sup A=1,\inf A = 0\)。
证明:先证 \(\sup A = 1\)
-
\[\forall x\in A, x\le 1 \]
-
\[\forall \alpha < 1,取x_0=1\in A,x_0=1>\alpha \]
再证 \(\inf A = 0\)
-
\[\forall x \in A, x\ge 0 \]
-
\[\forall \beta>0,取 y_0=\frac{1}{\lfloor\frac{1}{\beta}\rfloor+1},则有 y_0<\beta \]
证明阿基米德性质
\(\forall x,y\in \R\),且 \(x>0\),一定 \(\exist n_0\in\Z^+\),s.t. \(n_0x>y\),证明:
令 \(A=\{nx|n\in \Z^+\}\),下用反证法证明。
假设上述结论不成立,即有 \(\forall n\in \Z^+\) 成立 \(nx\le y\),
故有 \(A\) 为一个非空的有上界实数集。
由确界原理知:\(\sup A\in \R\),不妨设 \(\sup A = \alpha\)。
因为 \(x>0\),所以 \(-x<0\),从而 \(\alpha-x<\alpha\)。
由于 \(\alpha = \sup A\),所以 \(\alpha - x\) 必不是 \(A\) 的上界。
所以 \(\exist m\in \Z^+\),s.t. \(\alpha -x<mx\),即 \(\alpha<(m+1)x\)。
因为 \((m+1)x\in A\),所以 \(\alpha<(m+1)x\) 与 \(\alpha\) 是上确界矛盾。
Dirichlet 函数
\(D:\R\to \R\)
Riemann 函数
\(R:[0,1]\to \R\)
隐函数
与显函数相对,无显式表达式,例如:\(x^2+y^2=1\)。
复合函数
其他
具有某些特性的函数
有界函数
设 \(f:A\to \R\) 是一个函数、
若 \(f(A)\) 是一个有界集,则称 \(f\) 是一个有界函数。
\(\Leftrightarrow \exist M>0,\forall x\in A,|f(x)|\leqslant M\)。
约定 \(\sup f(A)写成\sup_\limits{x\in A} f(x)\),称为 “\(f\) 在 \(A\) 上的上确界”。下确界类似。
单调函数
设 \(f:D\to \R\) 是一个函数。
若\(\forall x_1,x_2\in D,x_1<x_2\),有 \(f(x_1)\leqslant(\geqslant)f(x_2)\),称 \(f\) 在 \(D\) 上单增(减),简记作 \(f\nearrow\)(应该为一个往右弯曲的箭头)。
注意区分“单调递增”和“严格单调递增”(\(\uparrow\))。
反函数定理:若 \(f:D\to f(D)\) 是一个严格单增的函数,则 \(f\) 必存在反函数 \(g:f(D)\to D\),s.t.\(f\circ g=id_{f(D)}\),\(g\circ f=id_D\)。
证明:仅需证明 \(f:D\to f(D)\) 为单射。
反证法:若 \(f:D\to f(D)\) 不是单射,则存在 \(x_1,x_2\in D\) 且 \(x_1 \neq x_2\),s.t. \(f(x_1)=f(x_2)\),
于是若 \(x_1<x_2\),由 \(f\uparrow\)……矛盾。
下证 \(g\uparrow\):
任取 \(y_1,y_2\in f(D)\),满足 \(y_1<y_2\)。
\(\exist x_1,x_2\in D, \texttt{s.t.} x_1=g(y_1),x_2=g(y_2)\)。
因为 \(y_1<y_2\),所以 \(x_1<x_2\)。(\(x_1=x_2\) 不合题意,\(x_1>x_2\Rightarrow y_1>y_2\))。
2024.9.19
幂
\(\forall a, b\in \R,n\in\Z^+,b^{n}-a^n=(b-a)(a^{n-1}+a^{n-2}b+\dots+b^{n-1})\).
当 \(b>a>0,n\in \Z^{+}-\{1\}\) 时有 \(b^n-a^n<(b-a)\times n\times b^{n-1}\)。
命题:设 \(a>0,n\in \Z^{+}-\{1\}\),则 \(\exist! x\in \{y\in \R|y>0\}\),s.t. \(x^{n}=a\)。
证明:先证唯一性
假设有 \(x_1,x_2\in R\),s.t. \((x_1)^n=(x_2)^n=a\),则
\(0=a-a=(x_1)^n-(x_2)^n=(x_1-x_2)((x_1)^{n-1}+\dots+(x_2)^{n-1})\),故 \(x_1-x_2=0\),\(x_1=x_2\)。
再证存在性:
令 \(E=\{t\in\R|t>0 且 t^n<a\}\),
令 \(\tilde t=\frac{a}{a+1}\in\R\),则 \(0<\tilde t<1 且 \tilde t<a\),故 \((\tilde t)^n<\tilde t<a\),故 \(\tilde t\in E\),所以 \(E\neq\varnothing\)。
令 \(t^*=a+2\),下可证明 \(t^*\) 是 \(E\) 的一个上界。
\(t^*>a 且 t^*>1\),故 \((t^*)^{n}>t^*>a\)。
从而 \(\forall t\in E\),有 \(t^{n}<a<(t^*)^{n}\Rightarrow(t^*)^{n}>t^n\),从而 \(t^*\) 是 \(E\) 的一个上界。
从而 \(E\) 是一个有上界的非空实数集,由确界原理知 \(\sup E\in \R\)。
令 \(\sup E=\alpha\),首先 \(\alpha\geqslant \frac{a}{1+a}\),下证 \(\alpha^n=a\)。
假设 \(\alpha^n<a\),选取一个 \(h\in(0,1)且 h<\frac{a-\alpha^n}{n(1+\alpha)^{n-1}}\)。
于是 \((\alpha + h)^n-\alpha^n<hn(\alpha+h)^{n-1}<h\times n(1+\alpha)^{n-1}<a-\alpha^n\Rightarrow(\alpha+h)^n<a\)
\(\Rightarrow(\alpha+h)\in E\) 与 \(\alpha=\sup E\) 矛盾。
假设 \(\alpha^{n}>a\),令 \(k=\frac{\alpha^n-a}{n\alpha^{n-1}}\),则 \(0<k<\alpha\)。
如果 \(t\in \R\) 且 \(t\ge \alpha -k>0\),则有
\(\alpha^n-t^n\le \alpha^n-(\alpha-k)^n<k\times n\alpha^{n-1}=\alpha^n-a\Rightarrow t^{n}>a\Rightarrow t\not\in E\)
\(\Rightarrow \alpha-k\) 是 \(E\) 的一个上界,与 \(\alpha=\sup E\) 矛盾。
设 \(a>0,b\in \R\),定义 \(a^b\)
-
当 \(b\in \Z^+\) 时,\(a^b\triangleq a\times a\times\dots a\)(\(n\) 个 \(a\) 相乘)。
\(b=0,a^{0}\triangleq 1\)。
-
当 \(b\in \Z-\N\) 时,\(a^b\triangleq \frac{1}{a^{-b}}\)。
-
当 \(b=\frac{m}{n}\in Q,m\in\Z,n\in\Z^+\) 时 \(a^b=(a^{\frac{1}{n}})^m\)。
\[\begin{aligned} f:&\Q\to\R\\ &x\to a^x \end{aligned} \] -
当 \(b\in\R-\Q\) 时
\[a^b\triangleq \begin{cases} \sup\{a^x|x\in \Q 且 x<b\}&,a>1\\ \inf\{a^x|x\in\Q 且 x<b\}&,a\in(0,1) \end{cases} \]易证上述两个集合均非空。
奇(偶)函数
设 \(f:D\to \R\) 是一个函数,又设 \(D\) 关于原点对称(即 \(\forall x\in D,-x\in D\))。
若 \(\forall x\in D,f(-x)=-f(x)\),则 \(f\) 为奇函数。
若 \(\forall x\in D,f(-x)=f(x)\),则 \(f\) 为偶函数。
周期函数
(一般)又设 \(D\) 满足:\(\exist T\neq 0\),s.t. \(\forall x\in D, x+T\in D\),又 \(f\) 满足:\(\forall x\in D,f(x+T)=f(x)\),称 \(T\) 是 \(f\) 的一个周期。
(书上)设 \(f:D\to \R\) 是一个函数,\(D\) 满足 \(\exist \sigma >0,\forall x\in D,x\pm \sigma \in D\),又 \(f\) 满足:\(\forall x\in D,f(x\pm\sigma)=f(x)\),则称 \(f\) 是一个周期函数。
按照一般的定义,\(f:(0,+\infin)\to \R\) 也可以是周期函数(单侧)。
数列极限
设
称 \(\{a_n\}\) 是一个(实)数列,称 \(a_n\) 为数列 \(\{a_n\}\) 的通项。
注意:存在双侧数列,下标取遍 \(\Z\)。
设 \(\{a_n\}\) 是一个数列,若 \(\exist a\in \R\),使得 \(\forall(\epsilon\in \R且)\epsilon>0,\exist N\in\Z^+,\forall(n\in\Z^+且)n>N\),成立 \(|a_n-a|<\epsilon\),则称数列 \(\{a_n\}\) 收敛于 \(a\),记作 \(\lim_{n\to+\infin}a_n=a\),或 \(a_n\overset{n\to +\infin}{\longrightarrow} a(a_n\to a(n\to+\infin))\)。
否则,则称 \(\{a_n\}\) 发散:\(\forall a\in \R\),使得 \(\exist \epsilon_0>0,\forall N\in\Z^+,\exist n>N\),成立 \(|a_n-a|\ge\epsilon_0\)。
("\(\epsilon-N\)" 语言)
例题:书上 P22 例3~6。
收敛与发散
设 \(\{a_n\}\) 是一个数列。
收敛
若 \(\exist a\in \R\),有 \(\forall \epsilon>0,\exist N\in \Z^+,\forall n>N\),成立 \(|a_n-a|<\epsilon\),则称 \(\{a_n\}\) 收敛于 \(a\)。
若 \(\exist a\in \R\),有 \(\forall \epsilon>0\),\(\{a_n\}\) 中仅有有限多项不属于 \((a-\epsilon,a+\epsilon)\) 中,则称 \(\lim_{n\to +\infin}a_n=a\)。
发散
若 \(\forall a\in \R\),有 \(\exist \epsilon_0>0,\forall N\in\Z^+,\exist n_N>N\),成立 \(|a_{n_{N}}-a|\ge\epsilon_0\),则称 \(\{a_n\}\) 发散。
若 \(\forall a\in \R\),有 \(\exist \epsilon>0\),\(\{a_n\}\) 中有无限多项不属于 \((a-\epsilon,a+\epsilon)\) 中,则称 \(\{a_n\}\) 发散。
例
证明 \(\{(-1)^{n+1}\}\) 发散。
证:
-
\(a=1\),取 \(\epsilon_0=\frac{1}{2}>0\),\(\forall N\in\Z\),取 \(n_N=2N>N\),成立 \(|(-1)^{n_N+1}-1|=2\ge \frac{1}{2}=\epsilon\)。
由数列不以 \(a\) 为极限的定义得于是可得 \(1\) 不是 \(\{(-1)^{n+1}\}\) 的极限。 -
类似的,可以证明 \(a=-1\) 不是 \(\{(-1)^{n+1}\}\) 的极限。
-
\(a\neq 1\) 且 \(a\neq -1\),令 \(\epsilon_0=min\{|a-1|,|a+1|,\frac{1}{2}\}>0\),\(\forall N\in \Z^+\),取 \(n_N=2N>N\),成立 \(|(-1)^{n_N+1}-a|=|-1-a|\ge \epsilon_0\)。
于是可得,\(a\) 不是 \(\{(-1)^{n+1}\}\) 的极限。
综上所述,\(\{(-1)^{n+1}\}\) 发散。
另证:\(\lim_{n\to+\infin}a_{2n}=x\) 且 \(\lim_{n\to+\infin} a_{2n-1}=y\),则 \(\{a_n\}\) 收敛等价于 \(x=y\)。
子列
定义(书上 P31 定义 1)。
特别的,若 \(\{a_n\}\) 的子列 \(\{a_{n_k}\}\) 从第 \(i\) 项开始和 \(\{a_n\}\) 从第 \(j\) 项开始”一摸一样“,则称 \(\{a_{n_k}\}\) 是 \(\{a_n\}\) 的一个平凡子列。(注意:\(i,j\) 可以相同也可以不同,要求 \(n_i=j,n_{i+1}=j+1\dots\))即”去掉 \(\{a_n\}\) 中有限多项得到平凡子列 \(\{a_{n_k}\}\)“。否则称为非平凡子列。
例题
P24 例8,例9
无穷大数列
\(\{a_n\}\) 是无穷大数列等价于 \(\lim_{n\to\infin}a_n=\infin\),定义为(”\(M-N\)“ 语言):
\(\forall M>0,\exist N\in\Z^+,\forall n>N(\Leftrightarrow n\in\cup(+\infin)\cap\Z^+\Leftrightarrow n\in(N,+\infin)\cap\Z^+)\),有 \(|a_n|>M\)。
称当 \(n\) 趋向于 \(+\infin\) 时,\(a_n\) 趋向于 \(\infin\)。记作 \(a_n\to \infin(n\to+\infin)\) 或把括号内的写在箭头上。
例:\(\{(-1)^nn\}\)。
另:正(负)无穷大数列……:\(\{n\}\)(\(\{-n\}\))。
收敛数列的性质
-
唯一性:若 \(\lim\limits_{n\to+\infin}a_n=a\in\R\) 且 \(\lim\limits_{n\to+\infin}a_n=b\in\R\),则 \(a=b\)。
证明:
\(\because\)\(\lim\limits_{n\to+\infin}a_n=a\in\R\) 且 \(\lim\limits_{n\to+\infin}a_n=b\in\R\)
\(\therefore\forall \epsilon>0\),\(\exist N_1\in\Z^+,\forall n>N_1\),有 \(|a_n-a|<\epsilon\),\(\exist N_2\in\Z^+,\forall n>N_2\),有 \(|a_n-b|<\epsilon\),
令 \(N=N_1+N_2\in\Z^+\),\(\forall n>N\) 有 \(|a-b|\le|a_{2N}-a|+|b-a_{2N}|<2\epsilon\) \(\Rightarrow a=b\)。
-
有界性:若 \(\lim\limits_{n\to+\infin}a_n=a\in\R\),则 \(\{a_n\}\) 有界。
证明:\(\because\)……特别地,取 \(\epsilon=1\),\(\exist N\in\Z^+,\forall n>N\),有 \(|a_n-a|<1\),即 \(|a_n|<|a|+1\)。
-
保号性:若 \(\lim\limits_{n\to+\infin}a_n=a>0(<0)\),则 \(\exist N\in\Z^+,\forall n>N\),有 \(a_n>(<)0\)。
证明:……特别地,取 \(\epsilon=\frac{a}{2}>0\),\(\exist N\in\Z^+,\forall n>N\),有 \(|a_n-a|<\epsilon=\frac{a}{2}\Rightarrow a_n>\frac{a}{2}>0\)。
-
保不等式性
若两数列存在极限且从某一项开始 \(a_n\le b_n\) 恒成立,则 \(a=\lim a_n\le \lim b_n=b\)(反证法:令 \(\epsilon=\frac{|b-a|}{3}\),\(n\) 足够大时 \(a_n\in(a-\epsilon,a+\epsilon)\),\(b_n\in(b-\epsilon,b+\epsilon)\),\(a_n\) 必然比 \(b_n\) 大)。
注意,就算 \(a_n<b_n\),极限也是 \(\le\),例如 \(\{\frac{1}{n+1}\}\) 和 \(\{\frac{1}{n}\}\)。
-
迫敛性(夹逼原则、两边夹法则)
设 \(\{a_n\},\{b_n\},\{c_n\}\) 是三个数列,若 \(\exist N_0\in\Z^+\),\(\forall n>N_0\) 有 \(a_n\le c_n\le b_n\),且 \(\lim\limits_{n\to+\infin}a_n=\lim\limits_{n\to+\infin}b_n=a\in\R\),则 \(\lim\limits_{n\to+\infin}c_n=a\)。
证明:\(\because\)…… \(a-\epsilon< a_n\le c_n\le b_n<a + \epsilon\)……
例
设 \(a_n\ge 0,n=1,2,\dots\),且 \(\lim\limits_{n\to+\infin}a_n=a\in \R\),证明 \(\lim\limits_{n\to+\infin}\sqrt {a_n}=\sqrt a\)。
证明:
-
若 \(a=0\),因为 \(\lim\limits_{n\to+\infin}a_n=0\),所以 \(\forall \epsilon>0,\exist N\in\Z^+,\forall n>N,|a_n|<\epsilon^2\Rightarrow |\sqrt{a_n}|<\epsilon\)。
-
若 \(a\neq 0\)(分母有理化),\(|\sqrt{a_n}-\sqrt a|=\frac{|a_n-a|}{|\sqrt{a_n}+\sqrt a|}\)。
\(\because \lim\limits_{n\to+\infin}a_n=a>0\),\(\therefore \exist N\in\Z^+,\forall n>N,a_n>\frac{a}{4}\Rightarrow\sqrt{a_n}>\frac{\sqrt{a}}{2}\Rightarrow0<\frac{1}{\sqrt{a_n}+\sqrt a}<\frac{2}{3\sqrt{a}}\)。
又 \(\forall \epsilon>0,\exist \tilde N>N,\forall n>\tilde N\) 有 \(|a_n-a|<\frac{3\sqrt{a}}{2}\times \epsilon\)……即证。
例(迫敛性)
证明 \(n^{\frac{1}{n}}\to 1(n\to +\infin)\)。
证明:令 \(h_n=n^{\frac{1}{n}}-1\),则 \(d\),则 \(0<h_n<\frac{2}{n}\)……
例
证明:\(\lim_{n\to+\infin}\frac{1}{\sqrt[n]{n!}}=0\)
证:\(\forall \epsilon>0\),因为 \(\lim_{n\to+\infin}\frac{\left(\frac{1}{\epsilon}\right)^n}{n!}=0\)(上节课证明过),
由极限定义知:
所以 \(\exist N\in\Z^+,\forall n>N\),有 \(\frac{\left(\frac{1}{\epsilon}\right)^n}{n!}<1\),即 \(\frac{1}{\sqrt[n]{n!}}<\epsilon\)。
或者用 Stirling 公式。
收敛数列四则运算
设 \(\lim_{n\to+\infin}a_n=a\in\R\),\(\lim_{n\to+\infin}b_n=b\in\R\),则:
-
\[\lim_{n\to+\infin}(a_n\pm b_n)=a\pm b \]
证明:
\[0\le|a_n+b_n-(a+b)|\le|a_n-a|+|b_n-b| \]两边的极限都是 \(0\)。
-
\[\lim_{n\to+\infin}(a_nb_n)=a\cdot b \]
证明:
\[\begin{aligned} 0\le|a_nb_n-ab|&=|a_nb_n-a_nb+a_nb-ab|\\ &\le|a_n||b_n-b|+|b||a_n-a| \end{aligned} \]两边极限都是 \(0\)。(\(a_n\) 有界,故可以找到绝对值的上界)。
-
若 \(\forall n\in\Z^+,b_n\neq 0,b\neq 0\),则有
\[\lim_{n\to+\infin}\frac{a_n}{b_n}=\frac{a}{b} \]
命题:数列 \(\{a_n\}\) 收敛 \(\Leftrightarrow\) \(\{a_n\}\) 的所有非平凡子列收敛。
证明:\(\Rightarrow\) 对于任意 \(\{a_{n_{k}}\}\) 是 \(\{a_n\}\) 的非平凡子列,总有 \(n_{k}\ge n\),易证。
\(\Leftarrow\) \(\{a_{2k}\},\{a_{3k}\},\{a_{2k-1}\}\) 都是 \(\{a_n\}\) 的非平凡子列。由题知:他们均收敛。
\(\{a_{6k}\}\) 是 \(\{a_{3k}\}\) 和 \(\{a_{2k}\}\) 的公共子列,且也是 \(\{a_{n}\}\) 的非平凡子列。设其极限为 \(a\)…… \(\{a_{2k}\},\{a_{3k}\}\) 极限均为 \(a\)。
又 \(\{a_{6k-3}\}\) 是 \(\{a_{2k-1}\}\) 和 \(\{a_{3k}\}\)……从而 \(\lim_{n\to+\infin}a_{2n-1}=a\)。
于是有 \(\lim_{n\to+\infin}a_n=a\)。
数列极限存在的一些判定条件
单调有界定理:
(在实数系中,)若 \(\{a_n\}\) 单调(递增/递减)有(上/下)界,则 \(\{a_n\}\) 收敛。
证明:
-
设 \(\{a_n\}\) 单增有上界,令 \(E=\{a_n|n\in \Z^+\}\sub \R\),且 \(E\neq \varnothing\) 且 \(E\) 有上界,有确界原理知:\(E\) 存在上确界,令 \(\alpha=\sup E\in \R\),下证明:\(\lim_{n\to+\infin}a_n=\alpha\)。
因为 \(\alpha=\sup E\),所以:
- \(\forall n\in\Z^+,a_n\le\alpha\)。
- \(\forall \epsilon>0,\exist a_{n_0}\in E\),使得 \(a_{n_{0}}>\alpha-\epsilon\)。
于是有对于任意的 \(\epsilon>0\),取 \(N=n_0\in\Z^+,\forall n>N\),有 \(a-\epsilon<a_{n_0}\le a_n\le \alpha\le\alpha+\epsilon\)。
即 \(|a_n-\alpha|<\epsilon\)。
-
单减同理。
-
例:\(a_n=\sum_{i=1}^n\frac{1}{n^2}\),证明其收敛。
只需证明 \(a_n\) 单增并用裂项相消求任意上界(比如 \(2\))。
-
例:\(a_{n}=\sum_{i=0}^n\frac{1}{n!}\),证明收敛。
单增。裂项,有上界 \(3\)。
-
P34 例三
-
重要极限:P34 例四
\(\forall n\in\Z^+\),令 \(b_n=\left(1+\frac{1}{n}\right)^n\),证明 \(\{b_n\}\) 收敛。
证明:\(b_1=2,n\in\Z^+-\{1\}\)。
\[\begin{aligned} b_{n}&=\left(1+\frac{1}{n}\right)^n\\ &=\sum_{k=0}^{n}\binom{n}{k}\left(\frac{1}{n}\right)^k\\ &=1+1+\sum_{k=2}^{n}\frac{n(n-1)\dots(n-k+1)}{k!n^k}\\ &=2+\sum_{k=2}^n\frac{1}{k!}(1-\frac{1}{n})\dots(1-\frac{k-1}{n})\\ b_{n+1}&=2+\sum_{k=2}^{n+1}\frac{1}{k!}(1-\frac{1}{n+1})\dots(1-\frac{k-1}{n+1}) \end{aligned} \]所以 \(\forall n\in\Z^+,b_n<b_{n+1}\)。
\[b_n\le2+\sum_{k=2}^n\frac{1}{k!}<3 \](由上面第二个例题知)故有界。
-
P35 例五,证明任意数列都存在单调子列。
致密性定理
任何一个有界数列必有收敛子列。
证明:任何数列必有单调子列(P35例五),该子列有界,故……
柯西收敛准则
P36
\(\{a_n\}\) 收敛等价于 \(\forall\epsilon>0,\exist N\in\Z^+,\forall n,m>N\) 有 \(|a_n-a_m|<\epsilon\),则称 \(\{a_n\}\) 是一个 Cauchy 列(基本列)。
等价定义:\(\forall\epsilon>0,\exist N\in\Z^+,\forall n>N,p\in \Z^+\) 有 \(|a_n-a_{n+p}|<\epsilon\)。
书上 P36 证明等价。
证明 Cauchy 列 \(\{a_n\}\) 有界:
特别地,对于 \(\epsilon=1\),有 \(\exist N\in\Z^+,\forall n>N,p\in\Z^+\),有 \(|a_{n+p}-a_n|<\epsilon\)
\(\Rightarrow \forall p\in\Z^+,|a_{N+1+p}|<|a_{N+1}|+1\),则其有界 \(\max\{|a_1|,|a_2|,\dots,|a_{N+1}|+1\}\)。
则由致密性定理知:存在子列 \(\{a_{n_k}\}\) 有极限 \(\zeta\)。
则 \(\forall \epsilon>0,\exist N\in\Z^+\),使得 \(\forall n>N\) 有 \(|a_n-\zeta|=|a_n-a_{n_{N+K}}+a_{n_{N+K}}-\zeta|\le|a_n-a_{n_{N+K}}|+|a_{n_{N+K}}-\zeta|<\epsilon\)。
习题课:
\(\sum_{i=1}^{n}\frac{1}{i}=\ln n+\epsilon_n\)
\(\sum_{i=1}^{n}(-1)^{i-1}\frac{1}{i}=(\sum_{i=1}^{2n}\frac{1}{i})-(\sum_{i=1}^{n}\frac{1}{i})=\ln 2+\epsilon_{2n}-\epsilon_n\)
确界原理 \(\Rightarrow\) 单调有界定理 \(\Rightarrow\) 致密性定理 \(\Rightarrow\) Cauchy 收敛准则。
证明:\(\{a_n=\sum_{k=1}^n\frac{1}{k}\}\) 不收敛
证:只需证明 \(\{a_n\}\) 不是柯西列
\(\exist \epsilon_0>0,\forall N\in\Z^+,\exist n_N>N,\exist p_N\in\Z^+\),有 \(|a_{n_N+p_N}-a_{n_N}|\ge \epsilon_0\)。
因为:\(1,\frac{1}{2},\frac13+\frac14,\frac15+\frac16+\frac17+\frac18,\dots\) 均大于等于 \(\frac12\)。
设 \(D\subseteq \R\) 且 \(x_0\in\R\),若 \(\exist\{x_n\}\) 满足 \(\forall n\in\Z^+,x_n\in D,\forall n,m\in\Z^+ 且 n\neq m,则 x_n\neq x_m\),且 \(\lim_{n\to+\infin}x_n=x_0\),则称 \(x_0\) 是 \(D\) 的一个聚点。
函数极限
设 \(f:D\to \R\) 是一个函数。
共 30 种可能。
先考虑极限存在的情况:
-
(\(\epsilon-M\) 语言)若 \(+\infin\) 是 \(D\) 的一个无限聚点,若 \(\exist a\in\R,\forall \epsilon>0,\exist M>0,\forall x\in D且 x>M\),有 \(|f(x)-a|<\epsilon\)。称 \(f\) 当 \(x\) 趋向于 \(+\infin\) 时以 \(a\) 为极限,记作 \(\lim_\limits{x\to+\infin\\x\in D}f(x)=a\)(\(x\in D\) 可不写)。
-
\(-\infin\) 类似 1。
-
若 \(\infin\) 是 \(D\) 的一个无限聚点,若…… \(\forall x\in D 且 |x|>M\) ……
例 证明:\(\lim_\limits{x\to+\infin}\frac{1}{x}=0\),\(\lim_\limits{x\to-\infin}\frac{1}{x}=0\),\(\lim_\limits{x\to\infin}\frac{1}{x}=0\)。
只证第一个:\(\forall \epsilon>0,\exist M=\frac1{\epsilon}\),则 \(\forall x>M\) 有 \(|\frac1x-0|=\frac{1}{x}<\frac1M=\epsilon\)。
-
(\(\epsilon-\delta\) 语言)若 \(x_0\) 是 \(D\) 的一个聚点,若 \(\exist a\in \R\),\(\forall \epsilon>0,\exist \delta>0,\forall x\in D 且 0<|x-x_0|<\delta\),有 \(|f(x)-a|<\epsilon\),称当 \(x\to x_0\) 时以 \(a\) 为极限,记作 \(\lim_\limits{x\to x_0}f(x)=a\)。
-
若 \(x_0\) 是 \(D\) 上一个聚点且 \(\exist\{x_n\}\) 两两不同,\(x_n>x_0\) 且 \(x_n\in D\),s.t. \(\lim_\limits{n\to+\infin}x_n=x_0\),若 \(\exist a\in \R\),\(\forall \epsilon >0,\exist\delta>0,\forall x\in D 且 0<x-x_0<\delta\),有 \(|f(x)-a|<\epsilon\),则称 \(f\) 当 \(x\to x_0+\) 时以 \(a\) 为极限,记作 \(\lim_\limits{x\to x_0+}f(x)=a\)。
-
类似 5。
函数极限的性质
以下为了方便总假设 \(f\) 在 \(\mathring{U}(x_0;\tilde\delta)\) 上有定义(\(x_0\in\R,\tilde\delta>0\))。
-
唯一性:若 \(\lim_{x\to x_0} f(x)=a\in\R\),又 \(\lim_{x\to x_0} f(x)=b\in\R\),则 \(a=b\)。
-
局部有界性:若 \(\lim_{x\to x_0} f(x)=a\in\R\),则 \(\exist \delta>0,M>0,\forall x\in\mathring U(x_0;\delta)\),有 \(|f(x)|\le M\)。
-
局部保号性:若 \(\lim_{x\to x_0} f(x)=a\in\R\),且 \(a>0\),则 \(\exist \delta>0,\forall x\in\mathring U(x_0;\delta)\),有 \(f(x)>\frac{a}{2}>0\)。\(a<0\) 同理。
-
局部保不等式性:若 \(\lim_{x\to x_0} f(x)=a\in\R,\lim_{x\to x_0} g(x)=b\in\R\),且 \(\exist \delta_1>0,\forall x\in\mathring U(x_0;\delta_1)\),有 \(f(x)\le g(x)\),则 \(a\le b\)。(反过来叙述:若 \(a<b\),则 \(f(x)\le g(x)\))。
-
(迫敛性)夹逼原理:设 \(f,g,h\) 在 \(x_0\) 的一个去心邻域 \(\mathring U(x_0;\tilde\delta)\) 内有定义,且满足 \(\forall x\in\mathring U(x_0;\tilde\delta)\),有 \(f(x)\le g(x)\le h(x)\),又 \(\lim_{x\to x_0} f(x) = \lim_{x\to x_0} h(x)=a\in\R\),则 \(\lim_{x\to x_0}g(x)=a\)。
-
(四则运算):设 \(\lim_{x\to x_0}f(x)=a\in\R,\lim_{x\to x_0}g(x)=b\in\R\),则有
- \(\lim_{x\to x_0}(f(x)\pm g(x))=a\pm b\)。
- \(\lim_{x\to x_0} f(x)\cdot g(x)=ab\)。
- 若 \(b\neq 0\),则 \(\lim_{x\to x_0}\frac{f(x)}{g(x)}=\frac{a}{b}\)。
注意:需要保证极限均存在。
-
复合函数求极限的一些充分条件
例:若 \(\lim_{x\to a}g(x)=A,\lim_{y\to A}f(y)=B\),问:是否有 \(\lim_{x\to a}f(g(x))=B\)?
否,反例:
\[\begin{aligned} g(x)&\equiv 0\\ f(x)&=\begin{cases} 1&,y=0\\ 0&,y\neq 0 \end{cases} \end{aligned} \]设 \(\lim_{x\to a}g(x)=A,\lim_{y\to A} f(y)=B\),存在 \(a\) 的某个去心邻域 \(\mathring U(a)\),使得 \(\forall x\in\mathring U(a),g(x)\in D_f\),如果满足以下条件之一:
-
\(\exist a\) 的某个去心邻域 \(\tilde{\mathring{U}}(a)\sub \mathring U\),且 \(\forall x\in\tilde{\mathring U},g(x)\neq A\)。
证明:
\[\lim_{y\to A}f(y)=B\Leftrightarrow\forall \epsilon>0,\exist \delta>0,\forall y\in\{t\in D_f|0<|t-A|<\delta\},|f(y)-B|<\epsilon \]\[\lim_{x\to a}g(x)=A\Leftrightarrow\forall \delta>0,\exist \gamma>0,\forall x\in\{s\in D_g|0<|s-a|<\gamma\},|g(x)-A|<\delta \]由条件知 \(0<|g(x)-A|\),故可用变量替换 \(g(x)\)。
-
\(\lim_{y\to A} f(y)=f(A) 且 A\in \R\)。(常用)
-
\(A=\infin(+\infin 或 -\infin),B\in \R\)。
则有 \(\lim_{x\to a}f(g(x))=\lim_{y\to A}f(y)=B\)。(变量替换)
-
海涅定理(Heine Theorem)
设 \(f\) 在 \(\mathring U(x_0;\delta)\) 内有定义,则有
-
若 \(\lim_{x\to x_0}f(x)\) 存在,则 \(\forall \{x_{n}\}(x_n\in\mathring U(x_0;\delta))\) 且 \(\lim_{n\to +\infin}x_n=x_0\),由 \(\lim_{n\to+\infin}f(x_n)\) 存在且等于 \(\lim_{x\to x_0}f(x)\)。(易证)
-
若 \(\forall \{x_n\}(x_n\in\mathring U(x_0;\delta))\) 且 \(\lim_{n\to +\infin}x_n=x_0\),对应的函数值数列 \(\{f(x_n)\}\) 均收敛,则 \(\lim_{x\to x_0}f(x)\) 必存在。\(\exist a\in \R\),使得:
-
\(\lim_{n\to+\infin}f(x_n)=a\)。
证明:取 \(\{y_n\}\) 满足 \(y_n\in\mathring U(x_0;\delta)\) 且 \(\lim_{n\to +\infin}y_n=x_0\),由题意 \(\{f(y_n)\}\) 收敛,不妨设 \(\lim_{n\to+\infin}f(y_n)=a\in\R\)。
再任取 \(\{x_n\}\),满足 \(x_n\in\mathring U(x_0;\delta)\) 且 \(\lim_{n\to+\infin}x_n=x_0\),由题意 \(\{f(x_n)\}\) 收敛。
再任取 \(\{z_n\}\),\(z_{2k-1}=y_k 且 z_{2k}=x_k\),则满足 \(z_n\in\mathring U(x_0;\delta)\) 且 \(\lim_{n\to+\infin}z_n=x_0\),由题意 \(\{f(z_n)\}\) 收敛且极限与 \(\{f(y_n)\}\) 和 \(\{f(x_n)\}\) 相同,故 \(\lim_{n\to+\infin}f(x_n)=a\)。
-
\(\lim_{x\to x_0}f(x)=a\)。
若 \(f(x)\) 当 \(x\to x_0\) 时不以 \(a\) 为极限,则 \(\exist \epsilon_0>0,\forall \delta>\tilde\delta>0,\exist x\in\mathring U(x_0;\tilde\delta)\) 有 \(|f(x)-a|\ge\epsilon_0\)
依次取 \(\tilde\delta=\min\{\delta,\frac1n\}\)(\(n=1,2,\dots\)),\(\exist x_n\in\mathring U(x_0;\tilde\delta)\),使得 \(|f(x_n)-a|\ge \epsilon_0\),则 \(x_n\in\mathring U(x_0,\delta)\),且 \(\lim_{n\to+\infin}x_n=x_0\),由 2.1 知 \(\{f(x_n)\}\) 收敛于 \(a\),与 \(|f(x_n)-a|\ge \epsilon_0\) 矛盾,故 \(\lim_{x\to x_0} f(x) = a\)。
-
柯西准则
设 \(f\) 在 \(\mathring U(x_0;\rho)\) 上有定义,则 \(\lim_{x\to x_0} f(x)\) 存在等价于 \(\forall \epsilon>0,\exist\delta >0,\forall x_1,x_2\in\mathring U(x_0;\delta)\),有 \(|f(x_1)-f(x_2)|<\epsilon\)。
(充分性好证)
必要性证明:
在 \(\mathring U(x_0;\rho)\) 中任取一个数列 \(\{x_n\}\) 满足 \(\lim_{n\to+\infin}x_n=x_0\),……,从而得到 \(\{f(x_n)\}\) 是一个 Cauchy 列,由数列极限的柯西收敛原理知:\(\{f(x_n)\}\) 收敛,设为 \(\lim_{n\to+\infin}f(x_n)=a\in\R\)。
对于题设中的 \(\epsilon>0\),\(\exist N_1\in\Z^+,\forall n>N_1\),有 \(|f(x_n)-a|<\epsilon\)(且 \(x_{n}\in\mathring U(x_0,\delta)\)),\(\forall x\in\mathring U(x_0;\delta)\),有 \(|f(x)-a|\le|f(x)-f(x_{N+1})|+|f(x_{N+1})-a|<2\epsilon\)。
由题知:\(\lim_{x\to x_0}f(x)=a\)。得证。
重要极限
-
\(\lim_{x\to 0}\frac{\sin x}{x}=1\)
\(\forall x\in(0,\frac{\pi}{2}),\sin x<x<\tan x\),故 \(\cos x < \frac{\sin x}{x}<1\),当 \(x\to 0+\) 时,三者极限均为 \(1\)。
-
\(\lim_{x\to\infin}(1+\frac{1}{x})^x=e\)
证明基础:\(\lim_{n\to+\infin}(1+\frac{1}{n})^n=e\)。
书上 P54
无穷小量与无穷大量
无穷小量
设 \(x_0\in\R,\rho >0\) 为常数,\(f\) 在 \(\mathring U(x_0;\rho)\) 上面有定义,若 \(\lim_{x\to x_0}f(x)=0\),则称 \(f\) 为当 \(x\to x_0\) 时的无穷小量,记作 \(f(x)=o(1),x\to x_0\)
若 \(f\) 在某个 \(x_0\) 的上有界,则称 \(f\) 为当 \(x\to x_0\) 时的有界量。
无穷小量阶的比较
注意:两个无穷小量的比值可能不存在,这组无穷小量不能比较。
设 \(f,g\) 都是当 \(x\to x_0\) 时的无穷小量。
-
若 \(\lim_{x\to x_0} \frac{f(x)}{g(x)}=0\):则称当 \(x\to x_0\) 时,\(f\) 是 \(g\) 的高阶无穷小量,也称当 \(x\to x_0\) 时,\(g\) 是 \(f\) 的低阶无穷小量,记作 \(f(x)=o(g(x)),x\to x_0\)。
\(o(g(x))\) 的含义(“小欧 ”):
\[o(g(x))=\left\{在 \mathring U(x_0) 上有意义的 f|\lim_{x\to x_0}\frac{f(x)}{g(x)}=0\right\} \]所以上面的 \(=\) 其实是 \(\in\),只是记作 \(=\)。
例:\(o(x^2)+o(x)=o(x)\)。
-
若存在两个正数 \(K\le L\) 及一个 \(x_0\) 的去心邻域 \(\mathring U(x_0)\),使得 \(\forall x\in \mathring U(x_0)\),有 \(K\le\left|\frac{f(x)}{g(x)}\right|\le L\),则称 \(f\) 和 \(g\) 为当 \(x\to x_0\) 时的同阶无穷小量。
特别地,若 \(\lim_{x\to x_0}\frac{f(x)}{g(x)}=c\neq 0\),则 \(f\) 和 \(g\) 为当 \(x\to x_0\) 时的同阶无穷小量。
注意:\(x^2\) 和 \(x^2\sin\frac1x\) 不是 \(x\to 0\) 时的同阶无穷小量,但是 \(x^2\) 和 \(x^2(\sin\frac1x+2)\) 是 \(x\to 0\) 时的同阶无穷小量,即使他们相除的极限不存在。
若 \(\exist L>0\),以及一个 \(\mathring U(x_0)\),使得 \(\forall x\in \mathring U(x_0)\),有 \(|\frac{f(x)}{g(x)}|\le L\),则记作 \(f(x)=O(g(x)),x\to x_0\)(“大欧”,不要求 \(f,g\) 均为无穷小量)。(几乎不用)
-
等价无穷小量。
若 \(\lim_{x\to x_0}\frac{f(x)}{g(x)} = 1\),则称 \(f\) 和 \(g\) 为当 \(x\to x_0\) 时的等价无穷小量,记作 \(f(x)\sim g(x),x\to x_0\)。
等价替换定理:设 \(f,g,h\) 在 \(\mathring U(x_0)\) 上有定义,且 \(f(x)=o(1),x\to x_0\),\(g(x)=o(1),x\to x_0\),且 \(f(x)\sim g(x),x\to x_0\),则有:
- 若 \(\lim_{x\to x_0}f(x)h(x)=A\in \R\),则 \(\lim_{x\to x_0} g(x)h(x)=A\);
- 若 \(\lim_{x\to x_0}\frac{h(x)}{f(x)}=B\in\R\),则 \(\lim_{x\to x_0}\frac{h(x)}{g(x)}=B\)。
无穷大量
设 \(f\) 在 \(\mathring U(x_0,\rho),(\rho >0)\) 上有定义,若 \(\forall G>0,\exist 0<\delta <\rho,\forall x\in \mathring U(x_0,\delta)\),成立 \(f(x)>G\),则称 \(f\) 当 \(x\to x_0\) 时以 \(+\infin\) 为“极限”,记作 \(\lim_{x\to x_0}f(x)=+\infin\),(\(-\infin,\infin\) 同理)。
例:证明 \(\lim_{x\to+\infin}e^x=+\infin\)
证:
例:\(\lim_{x\to+\infin}a^x=+\infin\Rightarrow \lim_{x\to-\infin}a^x=0\)。
证:由题 \(\forall G>0,\exist M>0,\forall x>M,a^x>G\)。
所以 \(\forall \epsilon>0\),令 \(G=\frac{1}{\epsilon}>0,\exist M>0,\forall x>M\),有 \(a^x>G=\frac1\epsilon\),于是令 \(x=-t\),有 \(\frac{1}{a^t}>\frac1\epsilon\),\(\forall t<-M\),有 \(0<a^t<\epsilon\)。
渐近线
称 \(y=f(x),x\in D\) 的函数图像是一条“曲线”(平面曲线)。
- 连续曲线
- 光滑曲线
- 分段光滑曲线
如果点 \((x,y)\) 沿着曲线 \(y=f(x)\) 连续变化如下:
当点 \((x,y)\) 的两个坐标之一趋向于无穷时,此点到某一定直线 \(y=kx+b\)(或 \(x=C\)(\(C\) 是常数))的距离趋向于 \(0\),则称此直线为曲线 \(y=f(x)\) 的一条渐近线。
-
\(y=C\) 水平渐近线
-
\(x=C\) 垂直渐近线
若 \(\exist x_0\in D_f'\),且 \(\lim_{x\to x_0+}f(x)=\infin\)(或 \(\pm\infin\))或 \(\lim_{x\to x_0-}f(x)=\infin,\pm\infin\),称 \(x=x_0\) 为 \(y=f(x)\) 的垂直渐近线。
-
\(y=kx+b\) 斜渐近线..
\(k,b\) 为待定常数。
\[\begin{aligned} &\lim_{x\to +\infin}\frac{|f(x)-(kx+b)|}{\sqrt{1+k^2}}=0\\ \Rightarrow&\lim_{x\to+\infin}(f(x)-(kx+b))=0\\\end{aligned} \]若 \(\lim_{x\to+\infin}\frac{f(x)}{x}=k\in\R\) 且 \(\lim_{x\to +\infin}(f(x)-kx)=b\in\R\),则称 \(y=kx+b\) 是 \(y=f(x)\) 的一条(右)斜渐近线。
左渐近线同理。
例:求曲线 \(y=\frac{x^2}{\sqrt{x^2-1}}\) 的渐近线。
解:函数 \(y=\frac{x^2}{\sqrt{x^2-1}}\) 的定义域为 \((1,+\infin)\cup(-\infin,-1)\)。
\(\because \lim_{x\to1+}\frac{x^2}{\sqrt{x^2-1}}=+\infin,\therefore x = 1\) 是曲线 \(y=f(x)\) 的一条垂直渐近线。(\(x\to-1-\) 同理)
所以 \(y=x\) 是 \(y=f(x)\) 的(右)(斜)渐近线,左斜渐近线同理。
*例:求 \(y=\ln x\) 的渐近线。
解:\(\lim_{x\to0+}\ln x=-\infin\),所以 \(x=0\) 是 \(y=\ln x\) 的渐近线。
\(\lim_{x\to+\infin}\frac{\ln x}{x}=0\)(后面再证,\(\lim_{n\to+\infin}\frac{n^k}{a^n}=0\))……
函数连续定理
设 \(f:D\to\R\) 是一个函数,\(x_0\in D\),
若 \(\forall \epsilon>0,\exist \delta>0,\forall x\in U(x_0,\delta)\cap D\),有 \(|f(x)-f(x_0)|<\epsilon\),则称 \(f\) 在 \(x_0\) 处连续。
(孤立点的定义:设 \(D\) 是 \(\R\) 的一个非空子集,若 \(x_0\in D\) 且 \(\exist \delta >0\),s.t. \(U(x_0;\delta)\cap D=\{x_0\}\),则称 \(x_0\) 为 \(D\) 的一个孤立点。)
注:
- 若 \(x_0\in D'\),则 \(f\) 在 \(x_0\) 处连续 \(\Leftrightarrow\lim_{x\to x_0}f(x) =f(x_0)\)。
- \(f\) 在 \(D\) 的孤立点处“自动”连续
\(\forall x\in D,x_0\in D\),令 \(\Delta x=x-x_0\),称 \(\Delta x\) 为自变量 \(x\) 的增量
\(\forall y\in f(D),y_0\in f(D)\),令 \(\Delta y=y-y_0\),称 \(\Delta y\) 为因变量 \(y\) 的增量
称 \(\Delta y|_{x=x_0}\) 为函数 \(y=f(x)\) 在 \(x=x_0\) 处的函数增量。
若 \(f\) 在 \(x_0\) 处连续,则有 \(\lim_{x\to x_0}f(x)=f(\lim_{x\to x_0}x)\)。
右连续:\(\lim_{x\to x_0+}f(x)=f(x_0)\),左同理。
\(f\) 在 \(x_0\) 处连续等价于 \(f\) 在 \(x_0\) 处既左连续又右连续。
间断点(不连续点)及其分类
设 \(f:D\to \R\) 是一个函数。
(间断点的考虑范围是 \(D'\cup D\) 记作 \(\overline D\)(称作 \(D\) 的闭包))(\(D'\) 应该是 \(\{x|\forall \delta>0,U(x,\delta)\cap D\neq \varnothing\}\))
-
可弃间断点:若 \(\lim_{x\to x_0+}f(x)=\lim_{x\to x_0-}f(x)=a\),且 \(f(x)\) 在 \(x_0\) 处无定义或 \(a\neq f(x_0)\),则称 \(x_0\) 为 \(f(x)\) 的可弃间断点。
\[f(x)=\begin{cases}\frac{\sin x}{x}&,x\neq 0\\ 0&,x=0\end{cases} \]\(x=0\) 是 \(f(x)\) 可弃间断点。
-
跳跃间断点:若 \(\lim_{x\to x_0+}f(x)\neq\lim_{x\to x_0-}f(x)\),无论 \(f\) 在 \(x_0\) 处是否有定义,都称 \(x_0\) 为 \(f\) 的跳跃间断点。
\[f(x)=\begin{cases}e^x&,x>0\\0&,x\le 0\end{cases} \]\(x=0\) 是 \(f(x)\) 的跳跃间断点。
-
除去前两种(第一类间断点)的间断点都称为第二类间断点。
\(x=0\) 是 \(f(x)=e^{\frac1x}\) 的第二类间断点(右极限不存在)。
分段连续:\(f\) 在 \([a,b]\) 区间上仅有有限个间断点。
黎曼函数 \(R(x)\):\(\Q\cap(0,1)\) 为 \(R(x)\) 所有间断点且为可去间断点。
连续函数的性质
Th. 若 \(f\) 在 \(x_0\) 处连续,\(g\) 在 \(y_0=f(x_0)\) 处连续,且 \(g\circ f\) 在 \(x_0\) 处的某个邻域有定义,则 \(g\circ f\) 在 \(x_0\) 处连续。
连续函数的局部性质
-
局部有界性
-
局部保号性
-
四则运算
若 \(f,g\) 在 \(x_0\) 处连续,则 \(f\pm g,f\cdot g\) 在 \(x_0\) 处均连续。
进一步,若 \(g(x_0)\neq 0\),则 \(\frac{f}{g}\) 在 \(x_0\) 处也连续。
-
复合函数连续性
若 \(f\) 在 \(x_0\) 处连续,\(g\) 在 \(y_0=f(x_0)\) 处连续,且 \(g\circ f\) 在 \(U(x_0)\) 上有定义,则 \(g\circ f\) 在 \(x_0\) 处连续。
连续函数的基本性质
-
有界性定理
若 \(f\) 在 \([a,b]\) 上连续,则 \(f\) 在 \([a,b]\) 上有界。
证明:反证法,假设 \(f\) 在 \([a,b]\) 上无界,不妨设 \(f\) 在 \([a,b]\) 上无上界。
\(f\) 在 \([a,b]\) 上有上界 \(\Leftrightarrow \exist M>0,\forall x\in [a,b],\texttt{s.t.}f(x)\le M\)。
\(f\) 在 \([a,b]\) 上无上界 \(\Leftrightarrow \forall M>0,\exist x\in[a,b],\texttt{s.t.}f(x)>M\)。特别地,\(\forall n\in\Z^+,\exist x_n\in[a,b],\texttt{s.t.}f(x_n)>n(*)\)。
因为数列 \(\{x_n\}\) 中每一项均在 \([a,b]\) 中,所以 \(\{x_n\}\) 有界。
由致密性定理知,存在 \(\{x_n\}\) 的一个收敛子列 \(\{x_{n_k}\}\),不妨设其极限为 \(x_0\)。
又因为 \(\forall k\in \Z^+,a\le x_{n_k}\le b\),所以 \(a\le \lim_{k\to +\infin}x_{n_k}\le b\Rightarrow x_0\in[a,b]\),不妨设 \(x_0\in(a,b)\)(右连续左连续的要单独讨论)。
由题意知 \(f\) 在 \(x_0\) 上连续,故有 \(\lim_{k\to +\infin}f(x_{n_k})=f(x_0)\in\R\),又由 \((*)\) 知\(\lim_{k\to+\infin}f(x_{n_k})=+\infin\),矛盾。
-
最值定理
若 \(f\) 在 \([a,b]\) 上连续,则 \(f\) 在 \([a,b]\) 上可取到最大值和最小值,即 \(\exist x_1\in[a,b],\texttt{s.t.} f(x_1)=\sup f([a,b])\),\(\exist x_2\in[a,b],\texttt{s.t.} f(x_2)=\inf f([a,b])\)。
证明:由 1 和确界定理可设 \(f([a,b])\) 上确界为 \(\alpha\),下证 \(\exist x_1\in[a,b],\texttt{s.t.}f(x_1)=\alpha\)。
用反证法,假设 \(\forall x\in [a,b]\),均有 \(f(x)<\alpha\),令 \(g(x)=\frac{1}{\alpha-f(x)},x\in[a,b]\),有 \(\forall x\in [a,b],g(x)>0\) 且 \(g(x)\) 连续。
由有界性定理知,\(g\) 在 \([a,b]\) 上有上界,设为 \(G>0\),于是 \(\forall x\in [a,b]\) 有 \(0<g(x)=\frac{1}{\alpha-f(x)}\le G\),从而 \(f(x)\le \alpha-\frac{1}{G},\forall x\in[a,b]\),矛盾。
-
以下两个定理等价
-
介值定理
若 \(f\) 在 \([a,b]\) 上连续,由此可令 \(m=\min f([a,b]),M=\max f([a,b])\),则 \(\forall \mu\in[m,M],\exist x_0\in[a,b],\texttt{s.t.}f(x_0)=\mu\)。
推论:若 \(f\) 在 \([a,b]\) 上连续,则 \(f([a,b])=[m,M]\)。
-
根的存在性定理(零点存在性定理)
若 \(f\) 在 \([a,b]\) 上连续,且 \(f(a)\cdot f(b)<0\),则 \(\exist x^*\in(a,b),\texttt{s.t.}f(x^*)=0\)。
证明:不妨设 \(f(a)<0,f(b)>0\)。
令 \(E=\{x\in[a,b]|f(x)>0\}\),因为 \(b\in E\),所以 \(E\neq \varnothing\)。
又因为 \(\forall x\in E\),有 \(a\le x\le b\),所以 \(E\) 有界,由确界原理得 \(E\) 存在上下确界,设 \(\alpha=\inf E\in \R\)。
因为 \(f(a)<0\),又 \(f\) 在 \(a\) 处右连续,由局部保号性知,\(\exist b-a>\delta_1>0,\forall x\in[a,a+\delta_1)\),有 \(f(x)<0\),所以 \(\alpha\neq a\)。
因为 \(f(b)>0\) 又 \(f\) 在 \(b\) 处左连续,所以由局部保号性知,\(\exist \delta_2>0,\forall x\in[b-\delta_2,b]\),有 \(f(x)>0\),所以 \(\alpha\neq b\)(\(\because b-\frac{\delta_2}{2}\in E,\therefore b-\frac{\delta_2}{2}\ge\alpha\))。
下证 \(f(\alpha)=0\),用反证法,假设 \(f(\alpha)\neq 0\),不妨设 \(f(\alpha)>0\),因为 \(\alpha\in[a,b]\),所以 \(f\) 在 \(\alpha\) 处连续,于是由连续函数的局部保号性知,\(\exist\delta_3>0,\forall x\in U(\alpha,\delta_3),f(x)>0\),即 \(U(\alpha,\delta_3)\in E\),与 \(\alpha=\inf E\) 矛盾。当 \(f(\alpha)<0\) 时类似的可得出矛盾。
从而 \(f(\alpha)=0\),令 \(x^*=\alpha\) 即得结论成立。
-
例:设 \(a>1\),\(n\in\Z^+\),证明方程 \(x^n=a\) 有唯一正实根。
证:令 \(f(x)=x^n-a,f(0)=-a<0,f(2a)=(2a)^n-a\ge 2^n\cdot a-a>0\)……
例(不动点):设 \(a,b\in \R,a<b\),\(f\) 在 \([a,b]\) 上连续,且满足 \(f([a,b])\subseteq [a,b]\),证明:\(\exist x_0\in[a,b],\texttt{s.t.}f(x_0)=x_0\),这种 \(x_0\) 被称为 \(f\) 的不动点。
证明:令 \(g(x)=f(x)-x,x\in[a,b]\),\(g\) 在 \([a,b]\) 上也连续,且有 \(g(a)=f(a)-a\ge 0\),若 \(f(a)=a\),令 \(x_0=a\) 即可,若 \(f(b)=b\),令 \(x_0=b\) 即可,若 \(f(a)\neq a\) 且 \(f(b)\neq b\),则 \(g(a)>0,f(b)<0\),则……。
反函数连续性定理
(若存在反函数)
设函数 \(f:[a.b]\to f([a,b])\) 是连续函数且严格单调(不妨设单增),则 \(f^{-1}:f([a,b])\to[a,b]\) 一定存在(\(f\) 是一个双射),且在 \(f([a,b])\) 上连续,且 \(f^{-1}\) 与 \(f\) 严格单调性一致。
证明:因为 \(f\) 单增以及 \(f\) 连续,所以 \(f([a,b])=[f(a),f(b)]\),下面证明 \(f^{-1}\) 在 \((f(a),f(b))\) 上连续(\(f^{-1}\) 在 \(f(a)\) 处右连续,\(f(b)\) 处左连续类似证明)。
任取 \(y_0\in(f(a),f(b)),\exist x_0\in(a,b),\texttt{s.t.}f(x_0)=y_0,\forall \epsilon>0,\exist x_1\in(a,b),x_2\in(a,b),\texttt{s.t.}x_1<x_0<x_2\),且 \(x_0-x_1<\frac{\epsilon}2,x_2-x_0<\frac \epsilon 2\),设 \(f(x_1)=y_1,f(x_2)=y_2\),由 \(f\) 严格单增得:\(y_1<y_0<y_2\),令 \(\delta =\min\{y_0-y_1,y_2-y_0\}>0,\forall y\in(y_0-\delta,y_0+\delta)\sub(y_1,y_2)\),有 \(x=f^{-1}(y)\in(x_1,x_2)\Rightarrow|x-x_0|<\epsilon\),所以 \(f^{-1}\) 在 \(y_0\) 处连续。
基本初等函数在其定义域内是连续的
-
\(f(x)=C\)
-
\(f(x)=\sin x,\sec x,\cos x,\csc x,\tan x,\cot x\)
-
\(f(x)=e^x\)
\(e^{a+b}=e^ae^b\) 由有理数推广到实数。
证明 \(e^{\alpha\beta}=(e^{\alpha})^\beta\),先证 \(\ln x^{\alpha}=\alpha \ln x\),\(\alpha\in\N\Rightarrow \alpha\in \Z\Rightarrow\alpha \in \Q\),故 \(\ln (e^\alpha)^\beta=\beta\ln e^{\alpha}=\alpha\beta\ln e\)。
函数的一致连续性
设 \(f\) 在 \(D\) 上有定义,若 \(\forall \epsilon >0,\exist \delta >0,\forall x_1,x_2\in D且|x_1-x_2|<\delta\) 成立 \(|f(x_1)-f(x_2)|<\epsilon\),则称 \(f\) 在 \(D\) 上一致连续。
例:\(f(x)=\frac{1}{x}\) 在 \((0,1)\) 上连续,但不是一致连续。
例:\(f(x)=x\) 在 \(\R\) 上一致连续。
例:\(f(x)=x^2\) 在 \(\R\) 上不是一致连续。
证:\(\exist \epsilon_0=1,\forall \delta >0,\exist N\in\Z^+,\texttt{s.t.}\frac{1}{N}<\delta\),令 \(x_1=N+1+\frac{1}{N+1}\in \R,x_2=N+1\in \R\),满足 \(x_1-x_2=\frac{1}{N+1}<\frac1{N}<\delta\),但 \(|f(x_1)-f(x_2)|=|2+\frac{1}{(N+1)^2}|>\epsilon_0=1\)。
但是 \(f(x)=x^2\) 在 \([1,2]\) 上一致连续。
定理:设 \(f\) 在区间 \(I\) 上有定义,则 \(f\) 在 \(I\) 上一致连续 \(\Leftrightarrow\) 在 \(I\) 中任取两个数列 \(\{x_n\},\{\tilde x_n\}\),满足 \(\lim_{n\to+\infin}(x_n-\tilde x_n)=0\),则 \(\lim_{n\to+\infin}(f(x_n)-f(\tilde x_n))=0\)。
证:\(\Rightarrow\) 易证。
\(\Leftarrow\):用反证法,假设 \(f\) 在 \(I\) 上不一致连续,即 \(\exist \epsilon_0>0,\forall \delta >0,\exist \tilde x,\tilde{\tilde x}\in I 且 |\tilde x-\tilde{\tilde x}|<\delta\),成立 \(|f(\tilde x)-f(\tilde{\tilde x})|\ge \epsilon_0\),对于每个 \(\delta_n=\frac1n>0\),\(\exist \tilde x_n,\tilde{\tilde x_n}\in I\) 且 \(|\tilde x_n-\tilde{\tilde x_n}|<\delta_n\),成立 \(|f(\tilde x_n)-f(\tilde{\tilde x})|\ge \epsilon_0\),取这样的数列即证。
(一致连续性定理)Cantor 定理:设 \(a,b\in\R,a<b\),则 \(f\) 在 \([a,b]\) 上连续 \(\Leftrightarrow\) \(f\) 在 \([a,b]\) 上一致连续。
例:设 \(a,b\in]R,a<b\),\(f\) 在 \((a,b)\) 上一致连续 \(\Leftrightarrow\) \(\lim_{x\to a-}f(x),\lim_{x\to b+}f(x)\) 均存在且 \(f\) 在 \((a,b)\) 连续。
例(书上例 12):若 \(f\) 在 \(I_1,I_2\) 上都一致连续,且 \(I_1\cap I_2\neq \varnothing\),则 \(f\) 在 \(I_1\cup I_2\) 上一致连续。
(\(\lim_{x\to0}(1+x)^\frac1x=e\Rightarrow \lim_{x\to 0}\frac{\ln(1+x)}{x}=1,\lim_{x\to 0}\frac{e^{x}-1}{x}=1\))
(若 \(f\) 在 \(x_0\) 处连续,则 \(\lim_{x\to x_0} f(x)=f(x_0)\),否则一定不成立)
导数和微分
设 \(D\sub \R\) 且 \(D\neq \varnothing\),\(x_0\in \R\),若 \(\exist \delta>0\),s.t. \((x_0-\delta,x_0+\delta)\sub D\),则称 \(x_0\) 是 \(D\) 的一个内点,\(D\) 的所有内点组成的集合j记作 \(\mathring D\) 或 \(\operatorname{Int} D\),称 \(\mathring D\) 为 \(D\) 的内部。
设 \(y= f(x),x\in I\) 是一个函数(\(I\) 是一个区间),任取 \(\Delta x\neq 0\) 且 \(x+\delta x\in I\),称连接图像上两点的一条直线为曲线 \(y=f(x),x\in I\) 的一条割线。若当 \(\Delta x\to 0\) 时,割线 \(L_{割}\) 的极限位置存在,则称极限位置所在的直线为曲线 \(y=f(x),x\in I\) 在点 \((x_0,f(x_0))\) 处的切线。
从而,切线的斜率 \(k_{切}=\lim_{\Delta x\to 0}\frac{f(x+\Delta x)-f(x)}{\Delta x}\)(若右侧极限存在)(\(k_{切}\) 也可以作 \(k_T\)),从而切线为 \(y-f(x_0)=k_T(x-x_0)\)。
导数
设 \(f\) 在 \((x_0-\rho,x_0+\rho)\)(其中 \(\rho>0\))上有定义,若 \(\lim_\limits{x\to x_0}\frac{f(x)-f(x_0)}{x-x_0}\) 存在,则称 \(f\) 在 \(x_0\) 处可导,记 \(\lim_\limits{x\to x_0}\frac{f(x_0)-f(x)}{x_0-x}\) 为 \(f'(x_0)\)(莱布尼茨:\(\frac{dy}{dx}|_{x=x_0}=\frac{df}{dx}|_{x=x_0}\))
设 \(f\) 在 \([x_0,x_0+\rho)\)(其中 \(\rho>0\))上有定义,若 \(\lim_\limits{x\to x_0+}\frac{f(x)-f(x_0)}{x-x_0}\) 存在,则称 \(f\) 在 \(x_0\) 处右可导,记为 \(f'_+(x_0)\)。
左可导类似。
Th. 若 \(f\) 在 \(x_0\) 处可导,则 \(f\) 在 \(x_0\) 处一定连续。
证明:\(f\) 在 \(x_0\) 处可导 等价于 \(\lim_{x\to x_0}\frac{f(x)-f(x_0)}{x-x_0}=f'(x_0)\)。
Th. \(f\) 在 \(x_0\) 处可导 等价于 \(f\) 在 \(x_0\) 处既左可导又右可导且二者相等。
例:求 \(f(x)=e^x\) 导函数(需要 \(\lim_{x\to 0}\frac{e^x-1}{x}=1\))
例:求 \(f(x)=x^\alpha\) 导函数。
解:
-
若 \(\alpha=0\)……
-
若 \(\alpha\ne 0,\forall x\in(0,+\infin)\),有
\[\begin{aligned} &\lim_{x\to x_0}\frac{x^\alpha-x_0^\alpha}{x-x_0}\\ =&\lim_{x\to x_0}\frac{e^{\alpha\ln x}-e^{\alpha\ln x_0}}{\alpha\ln x-\alpha\ln x_0}\cdot\frac{\ln x-\ln x_0}{x-x_0}\cdot \alpha\\ =&x^\alpha\cdot x^{-1}\cdot\alpha \end{aligned} \]其中 \(\lim_{x\to x_0}\frac{\ln x-\ln x_0}{x-x_0}=\lim_{x\to x_0}\frac{\ln(1+\frac{x}{x_0}-1)}{\frac{x}{x_0}-1}\times \frac{1}{x_0}=\frac{1}{x_0}\)。
如果存在一个邻域 \(U(x_0)\) 使得 \(f\) 在 \(U(x_0)\) 上有定义且 \(\forall x\in U(x_0)\) 有 \(f(x)\le f(x_0)\)。则称 \(x_0\) 是 \(f\) 的极大值点,\(f(x_0)\) 称为极大值。(极小值同理)极大值点和极小值点统称为极值点,极大值和极小值统称为极值。
费马引理:若 \(f\) 在 \(U(x_0)\) 上有定义且 \(x_0\) 是 \(f\) 的一个极值点,又 \(f\) 在 \(x_0\) 处可导,则 \(f’(x_0)=0\)。
证明:(极大值点)\(f'_+(x_0)\le 0,f'_-(x_0)\ge 0\),又二者相等……。
Th. (导函数的介值定理)(达布(Darboux)定理)设 \(a,b\in\R,a<b\),若 \(f\) 在 \([a,b]\) 上可导,且 \(f'_+(a)\neq f'_-(b)\),不妨设 \(f'_+(a)<f'_-(b)\),\(k\in(f'_+(a),f'_-(b))\),则至少存在一点 \(x_0\in(a,b)\),使得 \(f'(x_0)=k\)。
证:令 \(F(x)=f(x)-kx\),则 \(F(x)\) 在 \([a,b]\) 上可导,且 \(F'_+(a)=f'_+(a)-k<0,F'_-(b)=f'_-(b)-k>0\Rightarrow \exist x_1,x_2\in(a,b)且 x_1<x_2\) 使得 \(F(x_1)<F(a),F(x_2)<F(b)\),因为 \(F\) 在 \([a,b]\) 上可导,所以 \(F\) 在 \([a,b]\) 上连续。由最值 Th 知,\(F\) 在 \([a.b]\) 上取到最小值,即 \(\exist x\in[a,b]\) 使得 \(F(x_0)=\min F([a,b])\),满足 \(x_0\neq a,x_0\neq b\),由费马引理知 \(F'(x_0)=0\Rightarrow f'(x_0)=k\)。
求导法则:
-
四则运算(若 \(f,g\) 均在 \(x_0\) 处可导)
-
\((f\pm g)'(x_0)=f'(x_0)+g'(x_0)\)。
-
\((f\cdot g)'(x_0)=f'(x_0)g(x_0)+f(x_0)g'(x_0)\)。
\[\begin{aligned} &\lim_{x\to x_0}\frac{f(x)g(x)-f(x_0)g(x_0)}{x- x_0}\\ =&\lim_{x\to x_0}\frac{f(x)g(x)-f(x_0)g(x)+f(x_0)g(x)-f(x_0)g(x_0)}{x-x_0}\\ =&\lim_{x\to x_0}g(x)\cdot \frac{f(x)-f(x_0)}{x-x_0}+\lim_{x\to x_0} f(x_0)\frac{g(x)-g(x_0)}{x-x_0}\\=&f'(x_0)g(x_0)+f(x_0)g'(x_0) \end{aligned} \]
-
-
若 \(g(x_0)\neq 0\)
\((\frac{f}{g})'(x_0)=\frac{f'(x_0)g(x_0)-f(x_0)g'(x_0)}{[g(x_0)]^2}\)。