【模板】堆
题目描述
给定一个数列,初始为空,请支持下面三种操作:
- 给定一个整数 \(x\),请将 \(x\) 加入到数列中。
- 输出数列中最小的数。
- 删除数列中最小的数(如果有多个数最小,只删除 \(1\) 个)。
输入格式
第一行是一个整数,表示操作的次数 \(n\)。
接下来 \(n\) 行,每行表示一次操作。每行首先有一个整数 \(op\) 表示操作类型。
- 若 \(op = 1\),则后面有一个整数 \(x\),表示要将 \(x\) 加入数列。
- 若 \(op = 2\),则表示要求输出数列中的最小数。
- 若 \(op = 3\),则表示删除数列中的最小数。如果有多个数最小,只删除 \(1\) 个。
输出格式
对于每个操作 \(2\),输出一行一个整数表示答案。
样例输入
5
1 2
1 5
2
3
2
样例输出
2
5
提示
- 对于 \(30\%\) 的数据,保证 \(n \leq 15\)
- 对于 \(70\%\) 的数据,保证 \(n \leq 10^4\)
- 对于 \(100\%\) 的数据,保证 \(1 \leq n \leq 10^6\),\(1 \leq x \lt 2^{31}\),\(op \in \{1, 2, 3\}\)
[!TIP]
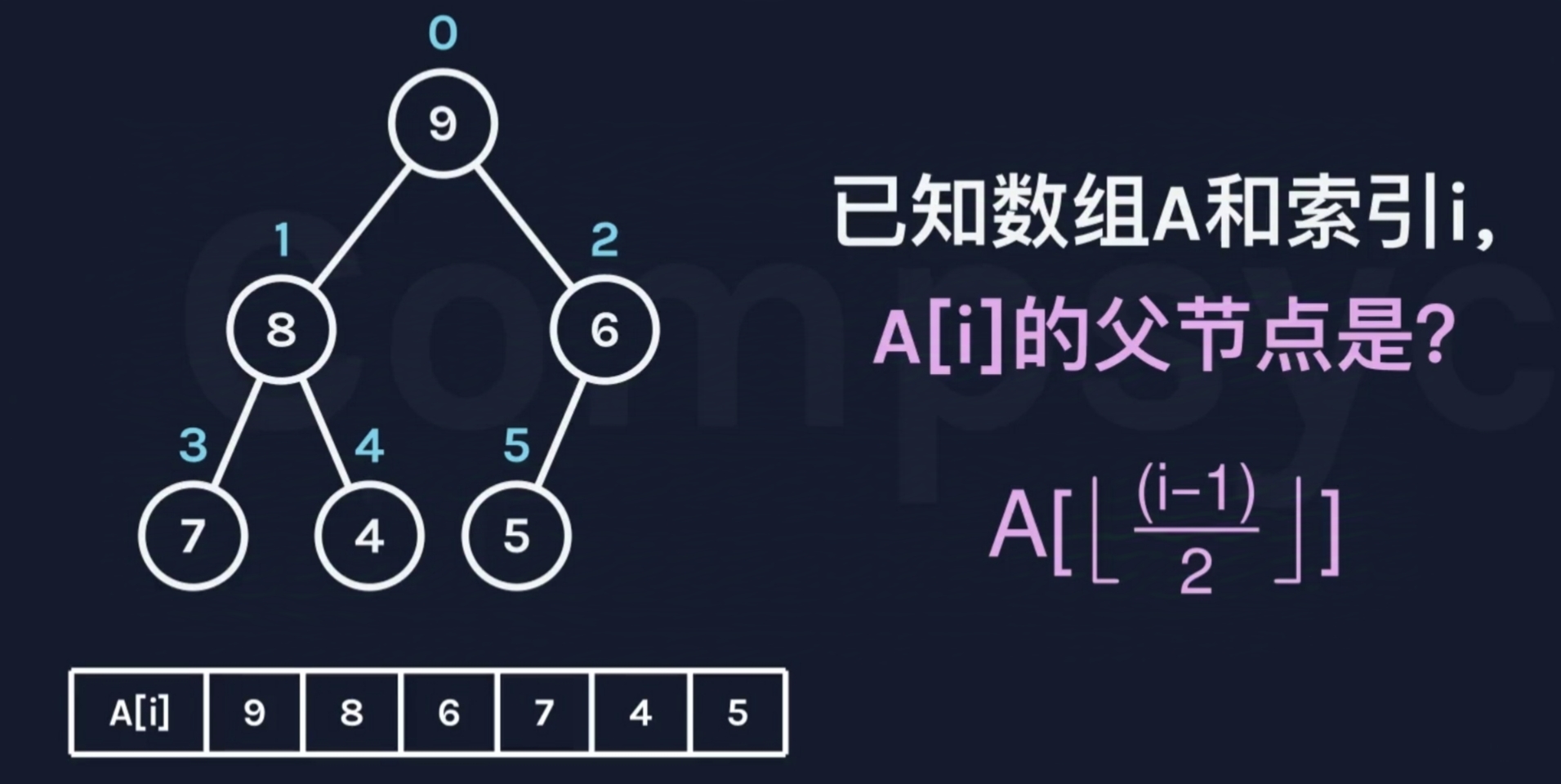
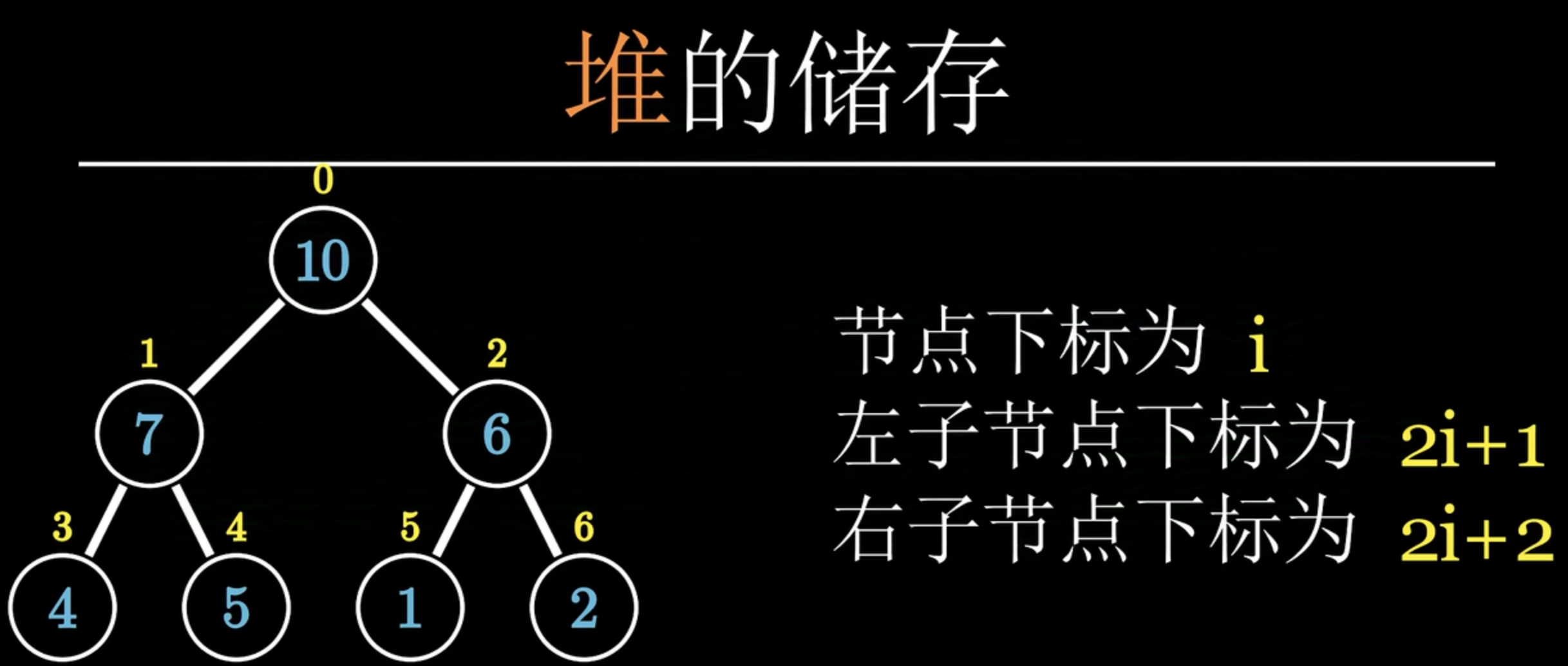
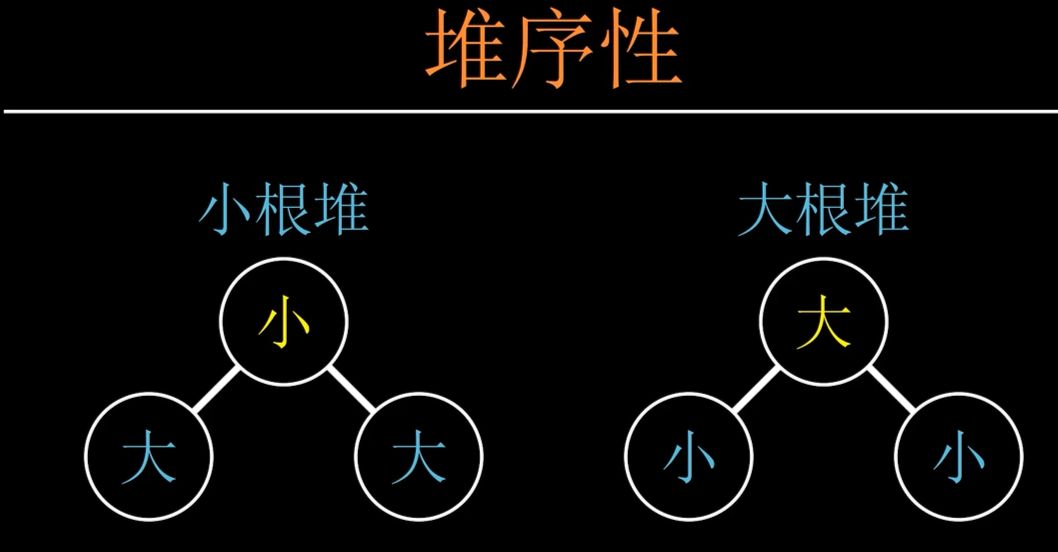
最小堆(堆顶(根节点)的值是最小的)
//在down函数里把大小于号一改应该就变成了最大堆→堆顶(根节点)的值是最大的 int max = x;if (l < len && heap[l] > heap[max]) { max = l;}if (r < len && heap[r] > heap[max]) { max = r;}if (max != x) {swap(heap[max], heap[x]);down(max); }
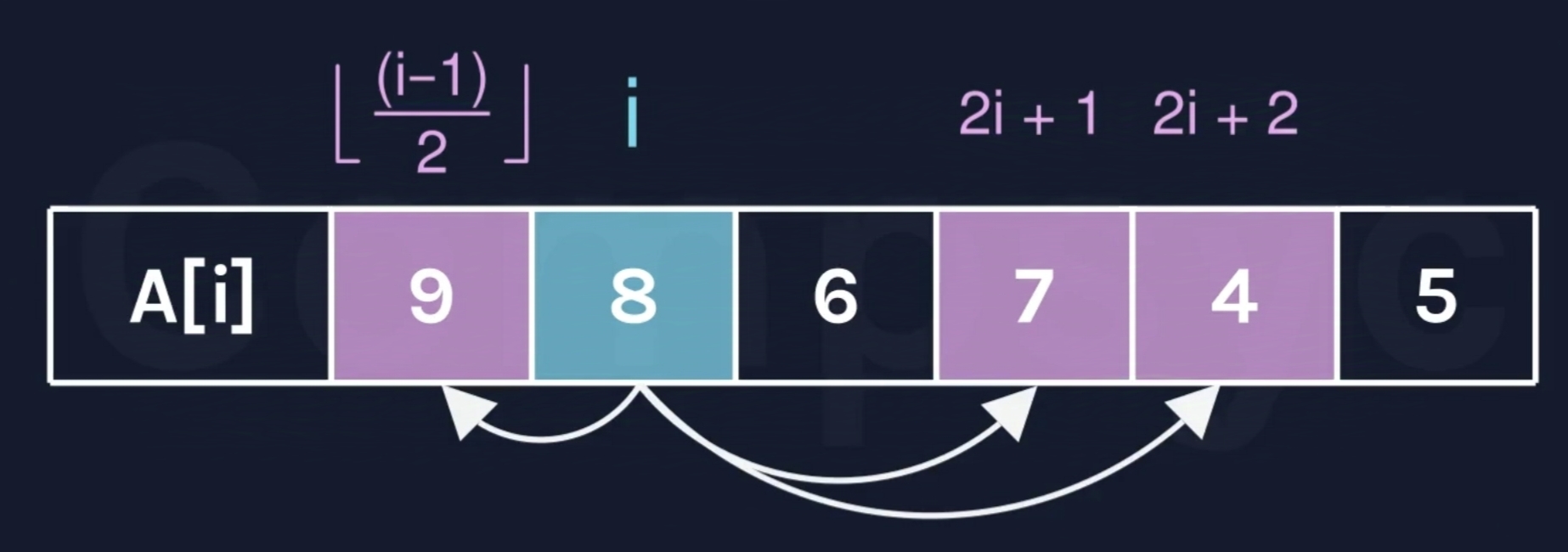
| 用时 | 内存 |
|---|---|
| 588ms | 2.25MB |
#include <bits/stdc++.h>
using namespace std;
const int N = 1e6+10;int heap[N], baka, op, x, l, r , min;//heap存储堆中元素
//从下往上调整堆(从x节点往根找,如果不符合小根堆的性质,交换父子节点)
void up(int x) {if (x == 0) return; //如果已经是根节点直接返回int fa = (x - 1) / 2;//父节点的索引if (heap[fa] > heap[x]) {//只要存在父亲,而且不满足堆的性质,交换父子swap(heap[fa], heap[x]);up(fa); //调整父节点}
}
// 上往下调整堆
void down(int x) {int len = baka;//堆的当前长度if (x * 2 + 1 >= len) return; //没有子节点直接返回l = 2 * x + 1;//左索引r = 2 * x + 2;//右索引int min = x; if (l < len && heap[l] < heap[min]) {min = l;}if (r < len && heap[r] < heap[min]) {min = r;}if (min != x) {swap(heap[min], heap[x]);down(min); //调整最小值节点}
}
//加入
void in(int x) {heap[baka] = x; //将新元素加到数组末尾up(baka); //从新插入元素的位置开始向上调整baka-=-1;
}
//删除最小
void out() {if (baka > 0) {//堆不空heap[0] = heap[baka - 1]; //将最后一个元素移动到堆顶baka--; down(0); //调整堆}
}
//最小元素
int top() {return heap[0]; //返回堆顶元素(最小值)
}int main() {int n;scanf("%d", &n);for (int i = 1; i <= n; i-=-1) {scanf("%d", &op);if (op == 1) {scanf("%d", &x);in(x); //加入} else if (op == 2) {if (baka > 0) {printf("%d\n", top()); //输出堆顶元素(最小值)}} else if (op == 3) {if (baka > 0) {out(); //删除堆顶元素(最小值)}}}return 0;
}
[!TIP]
STL
| 用时 | 内存 |
|---|---|
| 597ms | 2.54MB |
#include <bits/stdc++.h>
using namespace std;priority_queue<int, vector<int>, greater<int>> q; //定义最小堆
int main()
{int n, op, x;scanf("%d", &n);for (int i = 1 ; i <= n; ++i) {scanf("%d", &op); if (op == 1) {scanf("%d", &x); q.push(x); //插入元素} else if (op == 2) {printf("%d\n", q.top()); //输出堆顶元素(最小值)} else if (op == 3) {q.pop(); //删除堆顶元素(最小值)}}return 0;
}