二次函数+圆相结合的定值问题-编程知识

二次函数+圆相结合的定值问题

news/2024/11/29 19:02:16/文章来源:https://www.cnblogs.com/zhgmaths/p/18577373

专题：二次函数+圆题型：动点问题+定值问题难度系数：★★★★★

【题目】

（24-25九年级·湖北武汉）如图1，在平面直角坐标系$ xOy $中，开口向上的抛物线$ y=ax^2+bx+c $与$ x $轴交于$ A $，$ B(1,0) $两点，与$ y $轴交于点$ C $，且$ OA=OC=3OB $．

(1)求该抛物线的函数表达式；

(2)若点$ G $为抛物线上一点，当$ ∠GBA=∠BCO $时，直接写出点$ G $的坐标；

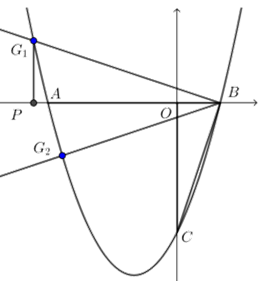
(3)如图2，若$ M $为线段$ AB $的中点，$ N $为抛物线的顶点，$ ⊙T $经过$ A $，$ B $，$ C $三点．经过圆心$ T $的直线交抛物线于$ D $，$ E $两点，直线$ ND $交$ x $轴于点$ P $，直线$ NE $交$ x $轴于点$ Q $．求$ MP·MQ $的值．

【详解】

（1）解：$ \because B(1,0) $，$ \therefore OB=1 $，

$ \therefore OA=OC=3OB=3 $，

$ \therefore A(-3,0) $，$ C(0,-3) $，

将$ A(-3,0) $，$ B(1,0) $，$ C(0,-3) $代入$ y=ax^2+bx+c $

得：$ \left{\begin{array}{c}
0=9 a-3 b+c \
0=a+b+c \
c=-3
\end{array}\right. $，解得$ \left{\begin{array}{c}
a=1 \
b=2 \
c=-3
\end{array}\right. $，

$ \therefore $该抛物线的函数表达式为$ y=x^2+2x-3 $；

（2）分析：$ ∠BCO $是已知角，易知$ G_1 $，$ G_2 $的大致位置，如下图，那如何求坐标呢？

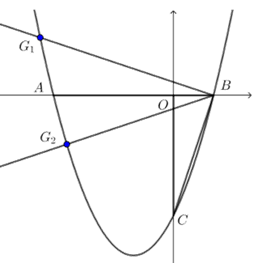
虽然$ ∠BCO $是已知角，但不是特殊角，下面有两种方法求解

方法1 构造全等三角形，取点$ M(-2,1) $，过点$ M $作$ MP⊥x $轴，易得$ △BOC≌△MPB $，再求出直线$ MB $方程，与抛物线解析式联立便可求出点$ G_1 $的坐标；同理求出点$ G_1 $的坐标.

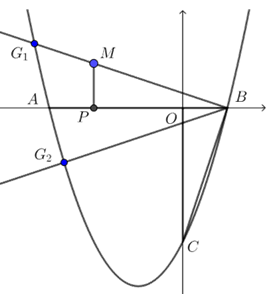
方法2 过点$ G_1 $作$ G_1 P⊥x $轴，易得$ △BOC∼△G_1 PB $，则$ \dfrac{G_1 P}{B P}=\dfrac{O B}{O C}=\dfrac{1}{3} $，

设$ G_1 (n,n^2+2n-3) $的坐标，

则$ \dfrac{G_1 P}{B P}=\left|\dfrac{n^2+2 n-3}{1-n}\right|=\dfrac{1}{3}. $，解得$ n=-\dfrac{10}{3} $或$ -\dfrac{8}{3} $，

则$ G_1\left(-\dfrac{10}{3}, \dfrac{13}{9}\right) $，$ G_2\left(-\dfrac{8}{3},-\dfrac{11}{9}\right) $.

等角问题，主要利用全等三角形或相似三角形处理；本题中显然相似三角形更简便.

（3）分析：求$ MP·MQ $的值，应该是个定值，即根据题中的运动情况求定值问题；

方法主要有代数法与几何法.

方法1 代数法

第一步：分析题中的运动情况

抛物线是确定的，$ A,B,C $三点是确定的，过该三点的圆是确定的，

根据三角形外接圆的定义可知，

圆心$ T $在$ AB $的垂直平分线$ x=-1 $，与$ AC $的垂直平分线$ y=x $的交点处，

$ \therefore T(-1,-1) $，

其他直线与点都是变化的，源头是直线$ TE $(绕着定点$ T $旋转的直线)，

第二步：分析所求的量

所求量为$ MP·MQ=|1+x_P ||1+x_Q |=|(1+x_P )(1+x_Q )| $，

第三步：引入变量

引入变量表示$ |(1+x_P )(1+x_Q )| $，

由于源头是直线$ TE $，可设直线$ TE $方程为$ y=k(x+1)-1 $，

引入的变量即$ k $，再想办法用$ k $表示$ x_P $与$ x_Q $，证明$ |(1+x_P )(1+x_Q )| $的结果与$ k $无关便可；

(也可想办法直接找到$ x_P $与$ x_Q $的关系，或设点$ E(n,n^2+2n-3) $，用$ n $表示$ x_P $与$ x_Q $)

直线若知道与一点，或两个点，直线方程便确定了，给引入变量提供思路.

如何$ k $表示$ x_P $与$ x_Q $呢？

那想下点$ P $与$ Q $是如何产生的就可知，

即要求出直线$ PN $与$ QN $方程$ ⇔ $由于点$ N $是定点，求出点$ D $、$ E $坐标（显然是用$ k $表示）.

分析动点的产生，“逆着回去分析”.

具体的解题过程

解：$ MP⋅MQ=\dfrac{16}{3} $；理由如下：

$ \because ⊙T $经过$ A $,$ B $,$ C $三点，

$ \therefore $ 圆心$ T $在$ AB $的垂直平分线$ x=-1 $，与$ AC $的垂直平分线$ y=x $的交点处，

选两条简单的直线求.

$ \therefore T(-1,-1) $．

设经过$ T(-1,-1) $的直线$ DE $解析式为$ y=k(x+1)-1 $，

直线方程采取了点斜式求解，快捷些.

联立得：$ \left{\begin{array}{c}
y=k(x+1)-1 \
y=x^2+2 x-3
\end{array}\right. $，即：$ x^2+(2-k)x-2-k=0 $ （※），

$ \because D $,$ E $为抛物线上两点，$ \therefore $设$ D(m,m^2+2m-3) $，$ E(n,n^2+2n-3) $，

$ \therefore m+n=k-2 $，$ mn=-k-2 $．

方程（※）很难解出来，故很难用$ k $表示点$ D $,$ E $的坐标，从而$ x_P $与$ x_Q $很难用$ k $表示；这里采取“设而不求”，用了韦达定理.

$ \because N $为抛物线的顶点，$ \therefore N(-1,-4) $，

$ \because D(m,m^2+2m-3) $，

$ \therefore l_{ND} $表示为$ y=\dfrac{m^2+2 m-3+4}{m+1}(x+1)-4 $，即：$ y=(m+1)(x+1)-4 $ ，

用了斜率公式与点斜式求直线方程.

$ \because $ 直线$ ND $交$ x $轴于点$ P $，

$ \therefore $ 令$ y=0 $，得$ (m+1)(x+1)-4=0 $，解得$ x_p=\dfrac{4}{m+1}-1 $，

$ \therefore M P=\left|x_p+1\right|=\left|\dfrac{4}{m+1}-1+1\right|=\left|\dfrac{4}{m+1}\right| $，

同理$ M Q=\left|\dfrac{4}{n+1}\right| $，

$ \therefore M P \cdot M Q=\left|\dfrac{4}{m+1}\right| \cdot\left|\dfrac{4}{n+1}\right|=\left|\dfrac{16}{(m+1)(n+1)}\right|=\left|\dfrac{16}{m n+m+n+1}\right| $$ =\left|\dfrac{16}{k-2-k-2+1}\right|=\dfrac{16}{3} $．

由韦达定理得到$ m $，$ n $的关系把结果化简得到$ MP⋅MQ $为定值.

故$ MP⋅MQ $的值为$ \dfrac{16}{3} $．

方法2 几何法

几何法想到了圆的相交弦定理（不太可能）、相似（尝试了直接找与$ MP $、$ MQ $有关的三角形或间接法，都失败）.

总结

第二问，处理同角问题，主要是利用全等三角形或相似三角形求解便可；
第三问，处理定值问题，首先要了解题中哪些量是确定的哪些是变化，变化的源头在哪里
处理定值问题，大致的思路是代数法与几何法：代数法优点是较为“套路”，即引入变量表示所求量证明其是定值（引入什么量简便，过程中有时候要采取“设而不求”的技巧），缺点是计算量可能较大；几何法主要是通过观察利用几何的知识点求解，优点是你观察出来的话解题过程会较为简便，缺点是题目复杂较难观察出来.
拓展知识：经过点$ A(x_1,y_1) $、$ B(x_2,y_2) $的直线斜率$ k=\dfrac{y_2-y_1}{x_2-x_1} $；直线的点斜式：若直线的斜率为$ k $，且经过点$ P(x_P,y_P) $，则直线方程为$ y=k(x-x_P )+y_P $.