https://codeforces.com/contest/2000/problem/E
题目描述
你非常喜欢屮大猩猩,于是你决定为它们组织一次拍摄活动。大猩猩生活在丛林中,丛林被表示为一个有 n 行 m 列的网格,有 w 个大猩猩同意参与拍摄,第 i 个大猩猩的身高ai .你希望将所有大猩猩放置在网格的单元格中,并且确保每个单元格中最多只有一只大猩猩。
每种方案的壮观程度等于网格中所有以 k 为边长的子正方形的壮观程度的总和
子正方形的壮观程度等于其中所有大猩猩的身高的总和
从所有合适的方案中选出最壮观的方案
输入格式
第一行包含一个整数 t ,表示共有 t 组测试样例
测试用例的描述如下
第一行包含三个整数 n,m,k表示网格的尺寸和子正方形的边长
第二行包含一个整数 w,表示大猩猩的数量
第三行包含 w 个整数 a1,a2,...,aw表示每个大猩猩的身高。
保证所有测试样例中 n⋅m的总和不超过 2e5,w的总和也不超过2e5
输出格式
对于每个测试用例,输出一个整数表示最壮观的方案的壮观程度
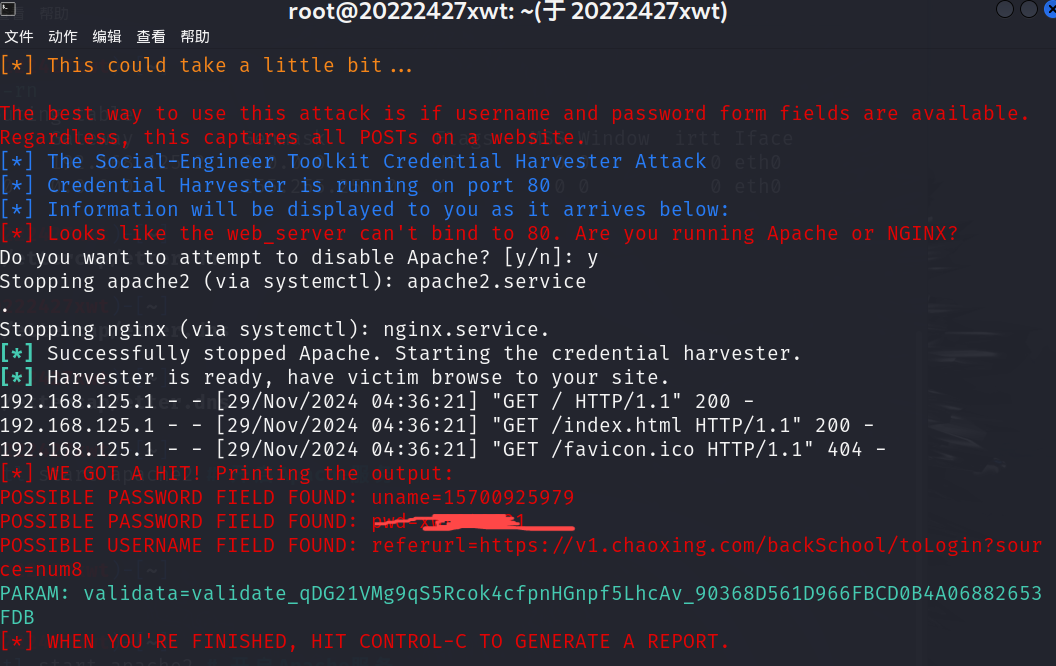
**输入 **
5
3 4 2
9
1 1 1 1 1 1 1 1 1
2 1 1
2
5 7
20 15 7
9
4 1 4 5 6 1 1000000000 898 777
1984 1 1
4
5 4 1499 2004
9 5 5
6
6 7 14 16 16 6
输出
21
12
49000083104
3512
319
[!TIP]
一个边长为k的正方形,开你是一个一个一个❤❤❤n*m的baka上从下往上扫,用矩阵最后一次扫到的位置减去矩阵第一次扫到的位置,然后加1,就可以得到答案(扫到的次数是横向扫到的次数*纵向扫到的次数)
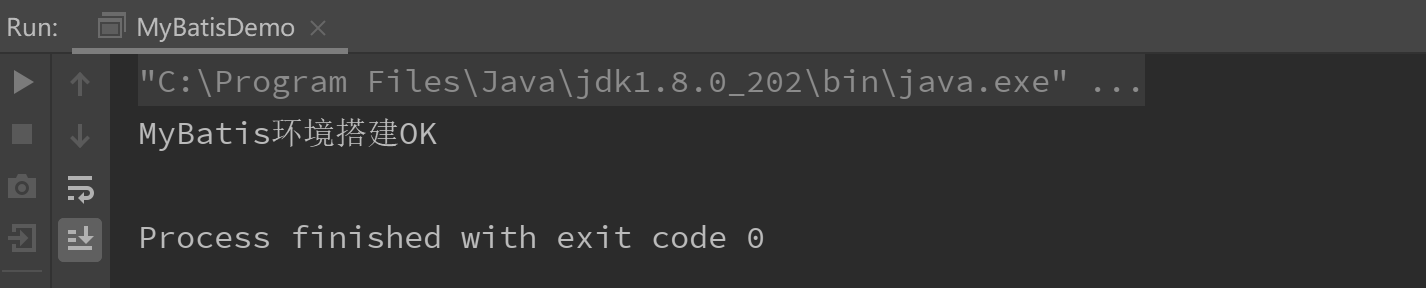
| 时间 | 内存 |
|---|---|
| 140ms | 1100KB |
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;int main()
{int t, n, m, k, w;scanf("%d", &t);for (int i = 0; i < t; i++) {scanf("%d %d %d %d", &n, &m, &k, &w);vector<ll> h(w);for (int i = 0; i < w; i++) {scanf("%lld", &h[i]);}vector<ll> baka;for (int x = 0; x < n; x++) //行❤{for (int y = 0; y < m; y++) //列❤{int r = k - 1;//在不超出网格右边界的情况下,从当前y坐标开始向右能放置的最大纵坐标(通过min(m - 1 - r, y)计算),再找到在不超出网格左边界的情况下,从当前y坐标开始向左能放置的最小纵坐标(通过max(0, y - r)计算),两者相减再加1就得到了水平方向上能放置完整子正方形的数量int l = min(m - 1 - r, y) - max(0, y - r) + 1;//横//在不超出网格下边界的情况下,从当前x坐标开始向下能放置的最大横坐标(通过min(n - 1 - r, x)计算),再找到在不超出网格上边界的情况下,从当前x坐标开始向上能放置的最小横坐标(通过max(0, x - r)计算),两者相减再加1就得到了垂直方向上能放置完整子正方形的数量int ww = min(n - 1 - r, x) - max(0, x - r) + 1;//竖,用矩阵最后一次扫到的位置减去矩阵第一次扫到的位置再+1baka.push_back(l * ww);//影响次数}}sort(baka.begin(), baka.end(), greater<ll>());//影响次数和身高降序排序sort(h.begin(), h.end(), greater<ll>());ll best = 0;for (int i = 0; i < w; i++)//贪心算法,每次选择最大的影响次数和最高的身高进行匹配 {ll a = baka[i];ll b = h[i];best += a * b;}printf("%lld\n", best);}return 0;