背景
记个笔记,这几天跟着这个教程到第五章了,顺带把递归和排序也看了(沙比学校天天整些屁事都没什么空折腾)。
String
字符串就直接用 GPT 生成了,这里就当文档记。(感觉没啥好说的)
- 字符串的输入和输出
输入字符串:使用 cin 输入字符串,注意会自动去除末尾的换行符。
std::string str;
std::cin >> str; // 只读取到第一个空白字符
输出字符串:使用 cout 输出字符串。
std::cout << str << std::endl;
- 字符串的长度
size() 或 length() 返回字符串的长度(字符个数),这两个方法是等效的。
std::string str = "Hello";
std::cout << str.size() << std::endl; // 输出 5
- 字符串的遍历
使用 for 循环或范围 for 遍历字符串中的每个字符:
for (char ch : str) {std::cout << ch << " "; // 输出每个字符
}
或者使用 for 循环结合索引:
for (int i = 0; i < str.size(); ++i) {std::cout << str[i] << " "; // 输出每个字符
}
- 字符串拼接(连接)
使用 + 操作符或 append() 方法:
std::string str1 = "Hello";
std::string str2 = "World";
std::string combined = str1 + " " + str2; // 拼接字符串
std::cout << combined << std::endl; // 输出 "Hello World"
append() 方法:
str1.append(" World"); // 向 str1 拼接 " World"
- 字符串查找
find() 查找子字符串在字符串中的位置,返回索引,找不到返回 std::string::npos。
std::string str = "Hello, World!";
size_t pos = str.find("World");
if (pos != std::string::npos) {std::cout << "'World' found at position: " << pos << std::endl;
} else {std::cout << "'World' not found!" << std::endl;
}
- 字符串替换
replace() 替换子字符串:
std::string str = "Hello, World!";
str.replace(7, 5, "C++");
std::cout << str << std::endl; // 输出 "Hello, C++!"
- 字符串比较
使用 ==、!=、<、>、<=、>= 运算符进行比较:
std::string str1 = "Hello";
std::string str2 = "Hello";
std::cout << (str1 == str2) << std::endl; // 输出 1,表示相等
- 字符串截取
substr() 截取子字符串:
std::string str = "Hello, World!";
std::string sub = str.substr(7, 5); // 从索引 7 开始,截取 5 个字符
std::cout << sub << std::endl; // 输出 "World"
最后是文档:
| 方法/操作 | 描述 | 示例代码 |
|---|---|---|
size() / length() |
获取字符串的长度 | std::string str = "Hello"; std::cout << str.size(); |
empty() |
判断字符串是否为空 | std::string str = ""; std::cout << str.empty(); |
append() |
向字符串后追加内容 | str.append(" World"); |
operator+ |
拼接两个字符串 | std::string str1 = "Hello", str2 = "World"; std::string result = str1 + " " + str2; |
find() |
查找子字符串,返回首次出现的位置 | std::string str = "Hello World"; size_t pos = str.find("World"); |
substr() |
获取子字符串 | std::string str = "Hello World"; std::string sub = str.substr(0, 5); |
replace() |
替换指定位置的字符或子字符串 | str.replace(0, 5, "Hi"); |
erase() |
删除字符串中的部分字符或子字符串 | str.erase(0, 5); |
at() |
通过位置访问字符(越界时会抛出异常) | std::string str = "Hello"; char c = str.at(1); |
operator[] |
通过索引访问字符(不安全,越界时不会抛出异常) | char c = str[1]; |
c_str() |
返回 C 风格的字符串指针(常用于与 C 函数交互) | const char* c_str = str.c_str(); |
compare() |
比较两个字符串 | std::string str1 = "abc", str2 = "abc"; str1.compare(str2); |
resize() |
改变字符串的大小(增加或减少) | str.resize(10, 'x'); |
insert() |
在指定位置插入子字符串 | str.insert(5, "Beautiful "); |
find_first_of() |
查找第一个出现的字符(从左到右) | str.find_first_of("aeiou"); |
find_last_of() |
查找最后一个出现的字符(从右到左) | str.find_last_of("aeiou"); |
to_string() |
将数字转换为字符串(C++11 起) | int x = 10; std::string str = std::to_string(x); |
stoi() |
将字符串转换为整数 | std::string str = "123"; int x = std::stoi(str); |
stoll() |
将字符串转换为长整型 | std::string str = "123456789"; long long x = std::stoll(str); |
stof() |
将字符串转换为浮点数 | std::string str = "3.14"; float x = std::stof(str); |
getline() |
从输入流中读取一行(通常与 cin 一起使用) | std::string line; std::getline(std::cin, line); |
to_upper() / to_lower() |
转换为大写或小写字母(需自行实现或使用库) | std::transform(str.begin(), str.end(), str.begin(), ::toupper); |
递归
流程
递归还是比较常见的,JS 里面也写过,但是用的不多(主要是 JS 写递归弄不好就爆栈了,能用但是得谨慎点),先简单过一下写法:
#include <iostream>using namespace std;int factorial(int number) {if (number == 0) {return 1;} else {return number * factorial(number - 1);}
}int main() {int number;cout << "Please enter a number: ";cin >> number;int result = factorial(number);cout << "The factorial is " << result << endl;
}
这是一个计算阶乘的代码,我们都知道阶乘是 n! = n × (n-1) × (n-2) × ... × 3 × 2 × 1 计算的,在 n > 0 的情况下是可以应用 f(n) = n * f(n-1) 的,这就可以使用递归实现。那么这段代码中的递归是如何计算的?以计算 3! 为例,调用 factorial(3)。
第一次调用 factorial(3):
-
n = 3,不满足 n == 0,进入 else 部分。
递归调用factorial(2),并保留当前的 n 值。
函数等待factorial(2)返回结果。
第二次调用factorial(2): -
n = 2,不满足 n == 0,进入 else 部分。
递归调用factorial(1),并保留当前的 n 值。
函数等待factorial(1)返回结果。
第三次调用factorial(1): -
n = 1,不满足 n == 0,进入 else 部分。
递归调用factorial(0),并保留当前的 n 值。
函数等待factorial(0)返回结果。
第四次调用factorial(0): -
n = 0,满足基准条件,返回 1。
递归的最深层结束,返回值为 1。
开始回溯并计算每层的结果:
-
回到
factorial(1):
factorial(1)得到factorial(0)的返回值1。
执行n * result = 1 * 1 = 1,返回1。
factorial(1)的计算结果是1,并将该结果返回给factorial(2)。 -
回到
factorial(2):
factorial(2)得到factorial(1)的返回值1。
执行n * result = 2 * 1 = 2,返回2。
factorial(2)的计算结果是2,并将该结果返回给factorial(3)。 -
回到
factorial(3):
factorial(3)得到factorial(2)的返回值2。
执行n * result = 3 * 2 = 6,返回6。
factorial(3)的计算结果是6。
再打个草稿,用脑子推一遍过程就是:
// 通式:f(n) = n * f(n - 1)f(3) = 3 * f(3 - 1) => 3 * f(2 * f(2 - 1)) => 3 * f(2 * f(1))f(3) = 3 * f(2 * f(1))f(3) = 3 * f(2 * 1)f(3) = 3 * 2 * 1 = 6
那么在执行的过程编译器干了什么呢?其实每一次递归调用都会创建一个新的栈帧,在栈帧中保存当前函数的局部变量和状态。每次递归调用的结果都会返回到上一层,直到最终返回到最初的函数调用,即递归调用的栈帧。递归栈的展开过程如下:
factorial(3)调用factorial(2)。factorial(2)调用factorial(1)。factorial(1)调用factorial(0)。factorial(0)返回1。factorial(1)返回1。factorial(2)返回2。factorial(3)返回6。
尾递归
但是这么做会不会很麻烦?调用完函数还要等返回,能不能直接把运算写在函数参数里面,免去最后的乘法那一步?有。请看这段写法:
int factorial_tail(int number, int acc = 1) {if (number == 0) return acc; // 基本情况,直接返回累积结果else return factorial_tail(number - 1, number * acc); // 尾递归调用
}
这段代码直接把运算后的结果丢在了 acc 里面,实际的执行流程是(还是以 3! 为例):
factorial_tail(3)调用factorial_tail(2, 3)。factorial_tail(2, 3)调用factorial_tail(1, 6)。factorial_tail(1, 6)调用factorial_tail(0, 6)。factorial_tail(0, 6)返回6。
欸?!这样做就不用再一直往上返回结果了。原来我们的写法 return number * factorial(number - 1) 在调用完函数还需要另外和 number 做运算,需要等待递归后的函数逐步返回结果。但如果我们直接把运算写在参数内,让他们在函数执行过程中完成这一步,就能省去这种操作。这种方式也被叫做尾递归。也就是递归调用在函数的最后一步,并且递归调用的结果直接返回,不需要再做任何额外的计算。
也就是说,只要递归调用是函数的最后一步、递归调用的结果直接返回给调用者、没有额外的操作(如加法、乘法等),递归调用的返回值就是最终的结果,那就是尾递归。相比常规的递归,递归调用后不再有其他操作,返回值就是递归调用的结果,而常规递归在递归调用后还需要执行其他操作(如加法、乘法等)。同时尾递归可以被编译器优化为迭代形式,从而避免了每次递归调用都在栈上分配新的栈帧,减少了内存的消耗和栈溢出的风险,也就是节省栈空间。另一点是避免栈溢出,如果递归调用的深度非常大,使用尾递归可以防止栈溢出(因为尾递归在某些编译器中可以被优化为迭代)。
(提一嘴,因为说到栈帧突然想到 i++ 和 ++i 的性能差异了,其实 ++i 会更好一点。使用 i++ 时,需要先保存 i 的原始值,这会生成一个 临时副本,然后再执行自增操作。在某些情况下,这会导致不必要的内存分配,增加一些额外的操作(如拷贝构造)而,++i 则直接修改 i 的值,返回的是 i 的引用,没有产生任何临时副本。所以,++i 通常比 i++ 稍微快一点)
排序
时间复杂度与空间复杂度
时间复杂度和空间复杂度在算法领域是经常见到的一个词,特别是 Leetcode、洛谷、ACM 这种平台就更多了。其实这两者就是一个描述算法执行时间和占用空间大小的概念,拿来衡量算法的一个标准。在进入排序(或者说学习所有算法)之前要知道一下这个,嘻嘻。
两者通常使用大 O 符号表示,也就是 O(n)。先说时间复杂度。大 O 里面的 n 就是指,一个算法执行所需的时间随着输入规模(通常表示为 n)变化的增长率,随着输入数据量增加,算法的执行时间如何变化。
如果是 O(1),也就是常数时间复杂度。无论输入大小如何,算法执行的时间始终是固定的。比如访问数组中的某个元素;如果是 O(log n),对数时间复杂度,那么算法的执行时间随着输入规模的增长而按对数比例增长。典型的例子是二分查找;如果是O(n),线性时间复杂度,那么算法的执行时间与输入规模成正比。比如线性搜索。
如果用坐标系表示出来,表示输入规模 n(也可以看作是问题规模的增长),随着 n 增加,图像上的点会沿着 x 轴从左到右移动;y 轴是算法的复杂度,这里的复杂度是以大 O 符号的阶数来描述的,比如 O(1)、O(n)、O(n²) 等。y 轴的数值反映了随着 n 增加,算法所需的时间或空间量。
当然,除了常数、对数和线性这三种复杂度以外,还有很多,看这个表格。
| 时间复杂度 | 描述 | 示例算法 | 效率 |
|---|---|---|---|
| O(1) | 常数时间复杂度 | 访问数组元素 | 高效 |
| O(log n) | 对数时间复杂度 | 二分查找 | 高效 |
| O(n) | 线性时间复杂度 | 线性搜索 | 中等 |
| O(n log n) | 线性对数时间复杂度 | 快速排序、归并排序 | 高效 |
| O(n²) | 平方时间复杂度 | 冒泡排序、选择排序 | 低效 |
| O(2^n) | 指数时间复杂度 | 递归算法(如斐波那契) | 低效 |
| O(n!) | 阶乘时间复杂度 | 排列、组合问题 | 极低 |
另外就是空间复杂度,一个算法在执行过程中所需的内存空间,随着输入规模的增加而增加的程度。也就是算法执行时,除了输入数据外,额外需要的存储空间。
| 空间复杂度 | 描述 | 示例算法 | 效率 |
|---|---|---|---|
| O(1) | 常数空间复杂度 | 原地排序 | 高效 |
| O(n) | 线性空间复杂度 | 需要存储数组或链表 | 中等 |
| O(n²) | 平方空间复杂度 | 存储二维矩阵、图 | 低效 |
一般情况下,时间复杂度是大多数情况下最被关注的,因为这直接表示了程序的执行效率,尤其是在数据规模很大时,优化时间复杂度是首要任务。而空间复杂度在内存有限或需要处理超大规模数据集时尤为重要,尤其是在嵌入式系统、大数据处理、图像处理和深度学习中,空间复杂度的优化常常与时间复杂度的优化同等重要。
冒泡排序
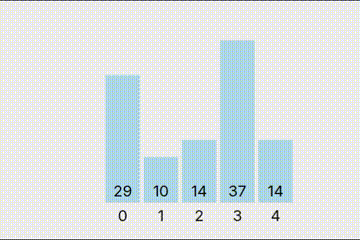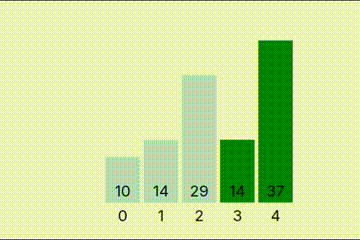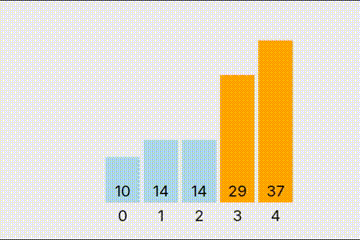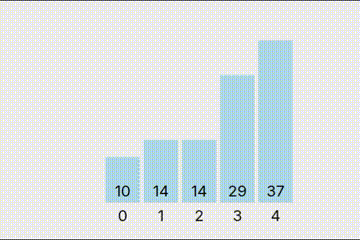
说完了复杂度这个基本的概念,就是排序算法了。冒泡排序是最经典的一种排序算法,甚至一些中学考试都会考这个。其基本原理就是一直比较相邻两个值的大小,如果左边的大于右边的,那就把左边的移到右边去,如此重复,最大的数像冒泡一样“冒”到最后,就是冒泡排序。
#include <iostream>
#include <vector>using namespace std;void bubbleSort(vector<int>& array) {int size = array.size();for (int i = 0; i < size; ++i) {for (int j = 0; j < size - i; ++j) {if (array[j] > array[j + 1]) {swap(array[j], array[j + 1]);}}}
}int main() {vector<int> array = {114, 514, 19, 1, 9, 81, 0};bubbleSort(array);for (int num: array)cout << num << endl;return 0;
}
最内层的循环负责交换数据,最外层的循环确保每个循环都能被遍历到。为啥要两层循环?举个例子,原数据是 [114, 514, 19, 1, 9, 81, 0],第一次内层循环是 [114, 19, 1, 9, 81, 0, 514],内层的循环只能确保相邻的两个数据交换,如果最开始连续多个数都是大值,就会出现例子那样的情况,数字 514 确实被冒到最后了,但是 114 还在最前面。这时候需要外层循环继续处理数据。
而外层循环的循环数根据数组长度 n = arr.size() - 1,内层循环的循环数是 n = arr.size() -1 - i。内层循环可以省掉外层循环的层数(也就是 ... - i)是因为冒泡排序每次内层循环处理完,最大数已经在最右边了,此时也就没有必要额外再进行比较。
回到这段代码中,bubbleSort 函数的参数处用的是 vector<int>& array 而非 vector<int> array。在 C++ 中,& 和 * 分别意味着取地址(在变量前使用这个符号表示获取该变量的内存地址)和解引用,但这是在变量中。在函数中,这两个符号的意味有一些不一样。& 表引用,在函数参数中,& 用于创建引用类型。引用本质上是给一个变量或对象起了一个别名,让你可以通过别名访问原对象。就如同代码中的 bubbleSort 函数是 void 类型的,而 main 函数调用 bubbleSort() 是没有定义变量接收返回值的。
冒泡排序的时间复杂度是 O(n²),优化后的冒泡排序的时间复杂度最好情况下是 O(n),最坏依旧是 O(n²)。优化后的冒泡排序也就是自动跳过已排序的层级(代码放下面)。空间复杂度是 O(1),因为冒泡排序属于那种原地排序的,没有额外使用数据结构。
#include <iostream>
#include <vector>using namespace std;void bubbleSortOptimized(vector<int>& array) {int size = array.size();for (int i = 0; i < size; ++i) {bool isSwapped = false;for (int j = 0; j < size - i; ++j) {if (array[j] > array[j + 1]) {swap(array[j], array[j + 1]);isSwapped = true;}}if (!isSwapped) {break;}}
}int main() {vector<int> array = {114, 514, 19, 1, 9, 81, 0};bubbleSortOptimized(array);for (int num: array)cout << num << endl;return 0;
}
如果数组已经是有序的,那么内层循环不会进行交换,isSwapped 会保持为 false,break 会提前终止排序,时间复杂度变成 O(n)。但如果数组是逆序的,最坏情况和普通冒泡排序一样,复杂度依旧是 O(n²),因为需要进行 O(n²) 次比较和交换。
选择排序
接下来是选择排序。选择排序就是从每次从为排列的数据中的最小值放到前面,以此类推循环下去。举个例子,假设数组 [5, 3, 7, 2, 6],按照选择排序的顺序来就是:
- 第一次外层循环,i = 0:
内层循环遍历[3, 7, 2, 6],比较这些值,最终找到最小值 2,并交换array[0]和array[3],得到[2, 3, 7, 5, 6]。 - 第二次外层循环,i = 1:
内层循环只比较[7, 5, 6],找到最小值 5,并交换array[1]和array[3],得到[2, 3, 5, 7, 6]。 - 第三次外层循环,i = 2:
内层循环只比较[7, 6],找到最小值 6,并交换array[2]和array[4],得到[2, 3, 5, 6, 7]。 - 第四次外层循环,i = 3:
内层循环只剩下一个元素 7,无需再交换,排序结束。
将以上逻辑转换为代码实现,大致结构就是两层循环,外层循环确定当前位置,内层循环比较待排序空间的最小值,然后通过一个变量存储最小数的索引,以此类推。
#include <iostream>
#include <vector>using namespace std;void selectionSort(vector<int>& array) {int size = array.size();for (int i = 0; i < size; ++i) {int minIndex = i;for (int j = i + 1; j < size; ++j) {if (array[j] < array[minIndex]) {minIndex = j;}}swap(array[i], array[minIndex]);}
}int main() {vector<int> array = {114, 514, 19, 1, 9, 81, 0};selectionSort(array);for (int num: array)cout << num << endl;return 0;
}
以上是大致实现(还可以进一步优化),最外层循环遍历数组的所有数,内部循环额外定义了索引 j,在这个区域内检索最小值,最后把最小值索引放到 minIndex 中,最后交换数据。选择排序的复杂度是 O(n²),空间复杂度是 O(1)。
插入排序
最后是插入排序。就像打扑克一样,从数组的第二个值开始一直与前面的元素进行比较,比前面的小就找合适的位置插进去。
#include <iostream>
#include <vector>using namespace std;void insertSort(vector<int>& array) {int size = array.size();for (int i = 1; i < size; ++i) {int key = array[i];int j = i - 1;for (; j >= 0 && array[j] > key; --j) {array[j + 1] = array[j];}array[j + 1] = key;}
}int main() {vector<int> array = {114, 514, 19, 1, 9, 81, 0};insertSort(array);for (int num: array)cout << num << endl;return 0;
}
首先,外层循环遍历所有数组元素,索引从 1 开始(因为插入排序是和前面的对比,当然如果要从 0 开始也行,反正后面都会排回来嘻嘻)。int key = array[i] 获取当前元素,随后定义一个内层循环 for (int j = 0; j >= 0 && array[j] > key; --j) 用于检测是否符合条件,如果符合条件,那就让开位置,把元素都放到后面去。 j >= 0 确保从数组的索引 0 开始查找;array[j] > key 确保当前元素比前面某个元素要小(否则没必要往前移)。最后通过 array[j + 1] = key 存回数值,但 j 是内层循环变量,此时提升作用域到内层循环外部以解决问题。
举个例子,假设待排序数组为 [5, 2, 9, 1, 5, 6]。
- 第一轮:从第二个元素 2 开始,将其与第一个元素 5 比较,发现 2 小于 5,于是将 5 向右移动,2 插入到最前面。数组变为
[2, 5, 9, 1, 5, 6]。 - 第二轮:将第三个元素 9 与前面已经排序的 5 比较,发现 9 大于 5,无需移动,数组保持不变 `[2, 5, 9, 1, 5, 6]。
- 第三轮:将第四个元素 1 与前面的元素依次比较,发现 1 比 9、5 和 2 都小,将它们依次向后移动,最后将 1 插入到最前面,数组变为
[1, 2, 5, 9, 5, 6]。 - 第四轮:将第五个元素 5 与前面的元素比较,发现它比 9 小,因此将 9 向后移,再与 5 比较,发现它们相等,不需要交换。数组变为
[1, 2, 5, 5, 9, 6]。 - 第五轮:将第六个元素 6 与前面的元素比较,发现它比 9 小,因此将 9 向后移,再与 5 比较,发现 6 比 5 大,于是插入到 5 后面,数组变为
[1, 2, 5, 5, 6, 9]。
插入排序的时间复杂度在最优情况下(已经有序的数组)的时间复杂度是 O(n),因为每次插入操作都不需要移动任何元素,最坏情况(反向排序的数组)下时间复杂度为 O(n²),因为每个数都需要移动。空间复杂度依旧是 O(1),文里提到的三个排序算法都是原地排序。
快速排序打算放到下一个笔记里面讲(和分治/二分一起嘻嘻)。