L. Recharge

给你三个整数,k,x,y。。x和y分别代表x个1和y个2 问你最多能凑出几个k
我们只需要考虑是否会出现浪费2的情况比如k=3 你此时没有1就只能用两个2来凑出这个3,这样就会浪费1.
我们把k分成奇偶数来看,如果k是偶数,那么百分百不会出现浪费,只需要把(y*2+x)/k就能得到结果
如果k是奇数,我们就需要考虑是否出现浪费,你凑出的每个k只要此时还有1,只需要一个1就可以少浪费一个2(2充足的前提下),因此我们二分答案
我们先考虑如果没有1的情况下mid个k所需要的最大sum值,也就是(mid+1)k,然后我们把当前mid和x取一个mid就是能减少多少y的浪费,sum就会变成(mid+1)k-min(mid,x);
代码:
点击查看代码
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll k,x,y;
ll sum=0;
bool check(ll x1)
{ll num=min(x,x1);ll sum1=(k+1)*x1-num;return sum>=sum1;
}
int main()
{ios::sync_with_stdio(0);cin.tie(0),cout.tie(0);ll t;cin>>t;while(t--){ cin>>k>>x>>y;ll c1=x,c2=y;if(k%2==0){ll sum=y*2+x;cout<<sum/k<<'\n';}else{ ll l=0,r=1e10;sum=x+y*2;while(l<r){ ll mid=(l+r+1)/2;if(check(mid)==true)l=mid;else r=mid-1;}cout<<l<<'\n';}}
}
G. Platform Game

本以为需要二分,结果是很简单的一道模拟
只需要先按照y的高度做一个降序排序,然后从上到下遍历先判断出小车当前位置,只要小车当前位置的p[i].l<=x<=p[i].r并且y>=p[i].y就代表他可以到这层,然后直接把小车的x位置
换到p[i].r因为它必会从这进入下一层
代码:
点击查看代码
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=2e5+10;
struct node{ll l,r,y;
}p[N];
bool cmp(node a,node b)
{return a.y>b.y;
}
int main()
{ios::sync_with_stdio(0);cin.tie(0),cout.tie(0);ll t;cin>>t;while(t--){ ll n;cin>>n;for(ll i=1;i<=n;i++){cin>>p[i].l>>p[i].r>>p[i].y;}ll x,y;cin>>x>>y;sort(p+1,p+1+n,cmp);
// cout<<x<<endl; ll nx=x,ny=y;ll q=0;for(ll i=1;i<=n;i++){ if(p[i].y<=y&&p[i].l<x&&p[i].r>=x){nx=p[i].r;ny=p[i].y;q=i+1;/// cout<<p[i].y<<" "<<p[i].l<<" "<<p[i].r<<endl;break;}}
// cout<<nx<<ny<<endl;for(ll i=q;i<=n;i++){if(p[i].y<=ny&&p[i].l<nx&&p[i].r>=nx){nx=p[i].r;ny=p[i].y;}}cout<<nx<<'\n'; }
}
E. Connected Components

题意:只要满足题目中所给公式中的任意一个,就可以加入到一个连通块中,如果一个点和一个联通块中的任意一点满足条件就可以把这个点加入到连通块中,问最少能分成几个这样的联通块。其实难点还是很明显的,就在于公式的推算把式子华为a[i]-i<=a[j]-j,i-b[i]>=j-b[j];
我们先按照式子中的a[i]-i进行结构体排序 然后进行整个结构体的遍历,是不是就能保证我们先遍历的编号就能满足第一个不等式。然后我们只需要找哪些点能满足第二个不等式就行。
因此我们用vector维护一个单调栈,让这个栈中元素head是大back是小每次从back开始看当前的i-p[i].r是否能与他们满足条件2连城一块,然后把能连的都连玩之后,把最小的也就是第一个遍历到的back元素pushback进去贪心的让后面的都尽量与他相连,最后看单调栈中剩下几个元素,就是答案
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int N=1e6+10;
typedef long long ll;
struct node{ll l,r;
}p[N];
bool cmp(node a,node b)
{if(a.l!=b.l)return a.l<b.l;else return a.r<b.r;
}
int main()
{ ios::sync_with_stdio(0);cin.tie(0) , cout.tie(0);ll n;cin>>n;for(ll i=1;i<=n;i++){cin>>p[i].l>>p[i].r;p[i].l-=i;p[i].r=i-p[i].r;}sort(p+1,p+1+n,cmp);vector<ll> v;for(ll i=1;i<=n;i++){ if(v.size()==0||v.back()>p[i].r)v.push_back(p[i].r);else{ ll num=v.back();while(v.size()!=0&&v.back()<=p[i].r){v.pop_back();}v.push_back(p[i].r);}}cout<<v.size()<<'\n';
}
//ai-i<=aj-j
//i-bi<=j-bj
D. Parallel Lines

因为保证了平面上一定有k条平行线,因此基本是明告诉你就是要你遍历整个图然后进行剪枝需要进行一个式子的推导
固定第一个点然后把所有点与第一个点相连,在每个点相连的时候暴力测试每个点与1号点相连时所有点中有几条线能与之平行
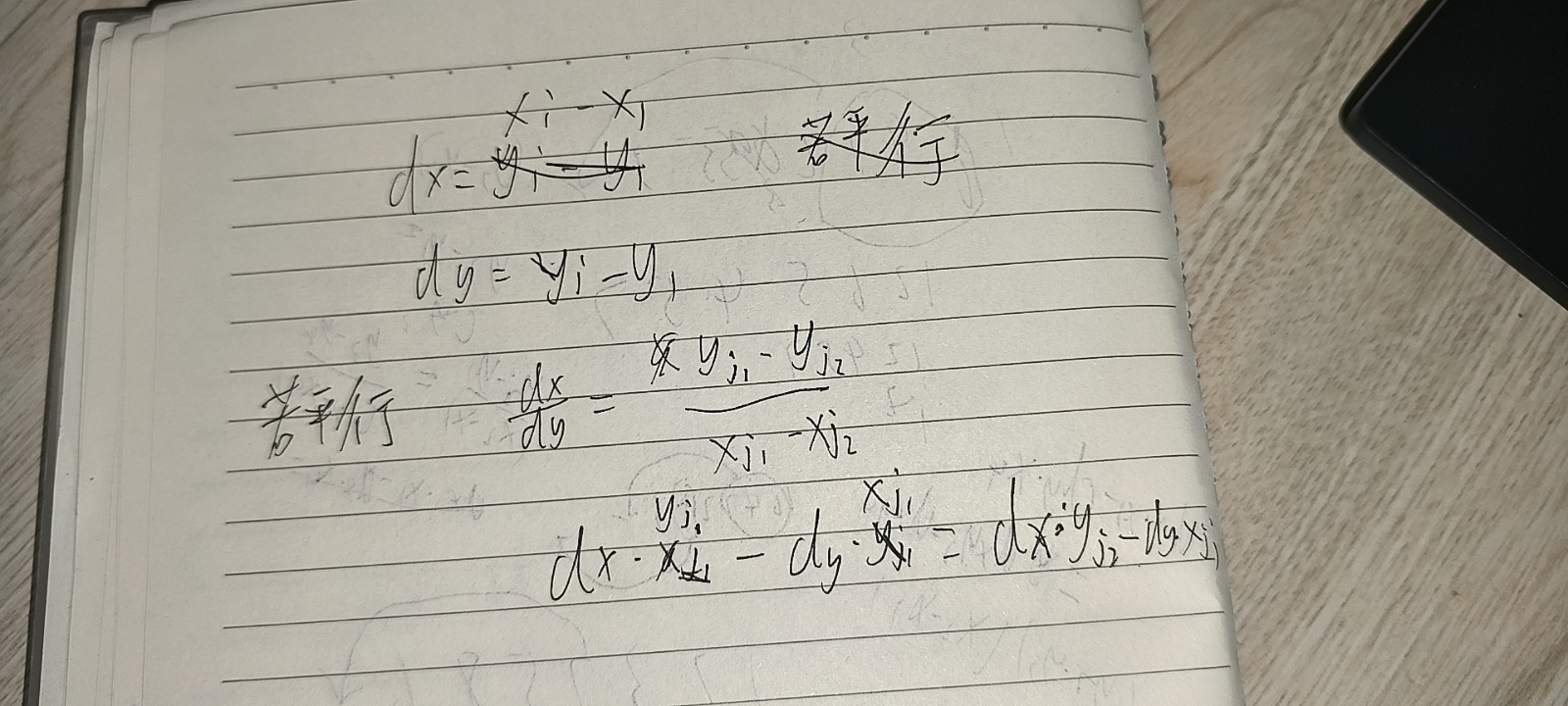
根据这个公式检测,如果够了k组平行的,并且k组中没有单独一个点的 就是正确答案并且输出
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int N=1e4+10;
typedef long long ll;
ll a[N];
pair<ll,ll>p[N];
int main()
{ ll n,k;cin>>n>>k;for(ll i=1;i<=n;i++){cin>>p[i].first>>p[i].second;}ll x1=p[1].first,y1=p[1].second;ll jud=0;ll jud1=0;for(ll i=2;i<=n;i++){ ll dx=p[i].first-x1;ll dy=p[i].second-y1;//cout<<dx<<" "<<dy<<endl; if(jud1==1)break;map<ll,vector<ll>>m1;// cout<<m1.size()<<endl;jud=0;for(ll j=1;j<=n;j++){ll k1=dx*p[j].second-dy*p[j].first;m1[k1].push_back(j);if(m1.size()>k)break; }if(m1.size()==k){ jud=0;for(auto w:m1){if(w.second.size()==1){jud=1;break;}}if(jud==0){ jud1=1;for(auto w:m1){cout<<w.second.size()<<" ";for(auto w1:w.second){cout<<w1<<" ";}cout<<'\n';}}
}}}
keep hard be the best