复数是为了解决无法对负数开根号的问题,其为实数的延伸:

复数表示为:
a + b i a+bi a+bi
其中 a 、b 为实数,i 为虚数单位,且 i 2 = − 1 i^2 = -1 i2=−1。实数 a 称为虚数的实部,b 称为虚数的虚部,实数可以被认为是虚部为零的复数。实部为零且虚部不为零的复数也被称作纯虚数;而实部不为零且虚部也不为零的复数也被称作非纯虚数。
- ( a + b i ) ± ( c + d i ) = ( a ± b ) + ( c ± d ) i (a+bi)\pm(c+di) = (a\pm b)+(c\pm d)i (a+bi)±(c+di)=(a±b)+(c±d)i
- ( a + b i ) ( c + d i ) = a c + a d i + b c i + b d i 2 = ( a c − b d ) + ( a d + b c ) i (a+bi)(c+di) = ac+adi+bci+bdi^2 = (ac-bd)+(ad+bc)i (a+bi)(c+di)=ac+adi+bci+bdi2=(ac−bd)+(ad+bc)i
- ( a + b i ) ( c + d i ) = ( a + b i ) ( c − d i ) ( c + d i ) ( c − d i ) = ( a c + b d ) + ( b c − a d ) i c 2 + d 2 = ( a c + b d c 2 + d 2 ) + ( b c − a d c 2 + d 2 ) i {(a+bi) \over (c+di)} = {(a+bi)(c-di) \over (c+di)(c-di)} = {(ac+bd)+(bc-ad)i \over c^2 + d^2} = {({ac+bd \over c^2 + d^2})+({bc-ad \over c^2 + d^2})i} (c+di)(a+bi)=(c+di)(c−di)(a+bi)(c−di)=c2+d2(ac+bd)+(bc−ad)i=(c2+d2ac+bd)+(c2+d2bc−ad)i
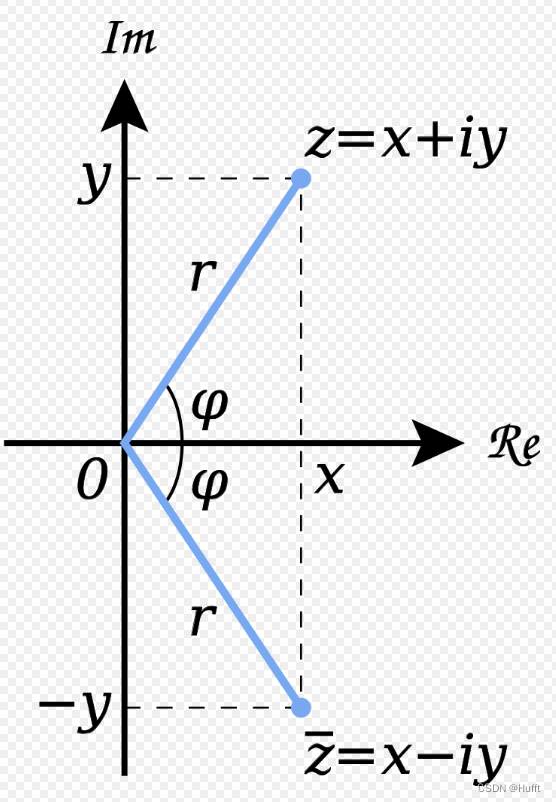
复平面
复平面是用水平的实轴与垂直的虚轴建立起来的复数的几何表示。两个复数乘法的几何表示:乘积的模长是两个模长的乘积,乘积的辐角是两个辐角的和。所以对一个复数逆时针旋转90都相当于对其乘 i
自然对数的底数 e e e
e ≈ 2.718281828459 … e\approx 2.718281828459… e≈2.718281828459…
常数 e 的含义是单位时间内,持续的翻倍增长所能达到的极限值。例如在银行年利率不变的情况下,假定为 r , 银行每年的付息次数为 n,则每次付的利息为 r n r\over n nr,则一年的总收益率为: ( 1 + r n ) n (1+{r\over n})^n (1+nr)n,则当 n 为无穷大时 lim n → ∞ ( 1 + 1 n ) n = e \lim \limits_{n \rightarrow \infty} (1+{1\over n})^n = e n→∞lim(1+n1)n=e,且有 lim n → ∞ ( 1 + r n ) n = e r \lim \limits_{n \rightarrow \infty}(1+{r\over n})^n = e^r n→∞lim(1+nr)n=er
欧拉公式
e i ϕ = c o s ϕ + i s i n ϕ e^{i\phi} = cos \phi + i\ sin\phi eiϕ=cosϕ+i sinϕ