MobiSys2022 CoDL论文详解

算子切分

在了解算子切分前，先了解一下卷积的运算过程，作者将算子切分分为了两个维度的切分：OC维度和H维度，没有W维度可能与数据在内存中的存储方式有关。

OC维度切分

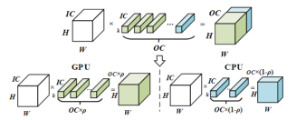
卷积就是OC数量个kernel_size×kernel_size×IC大小的卷积核与输入张量卷积计算后的输出叠加，因此从OC维度上切分，将OC×ρ个卷积核放在CPU上，OC×（1-ρ）个卷积核放在GPU上计算是容易理解的。

H维度切分

从H维度上切分，如果H * ρ = kerne_size + stride * n ，那切分与不切分的结果是可以等效的，负责就需要从切分位置进行填充，经过这一操作后，特征图也会增大。

不同维度划分对比

作者以YOLO中的卷积为例，测试了不同大小卷积通过两个维度切分后的加速效果对比，切分比例为0.5。文中给出的解释是：

The reason is that 𝐻 partitioning may reduce processor utilization compared to 𝑂𝐶, depending on the operator shape. To utilize the inter-core and intra-core parallelism of a processor, the tensors of an operator need to be divided into blocks and scheduled to run on different cores. Take the GPU as an example shown in Fig. 11. A block named as a work group is scheduled to run on a GPU core. To efficiently utilize the many ALUs in a core, the basic execution unit named as a warp executes the same instruction for a number of threads (e.g., 64 or 128) simultaneously. Therefore, a work group should provide enough threads to fill up the warps. Or there will be idle ALUs.

作者提出与 OC 相比，H 分区可能会降低处理器利用率，计算任务分配给SM，每一个SM会有32个线程束，每一个线程数有64或者128线程，每一个线程在一个ALU上计算，线程较少，一些ALU会空闲。（这里建议看一下OPenCL后端怎么进行矩阵乘的）

Op_chain

Op

我们已经理解了算子切分，算子切分会带来一些开销，其中包括CPU和GPU的数据转化，数据的映射的开销。如果一个算子进行一次划分，那么数据映射带来的开销势必会非常大，因此将多个算子链接起来形成Op_chain，只在链头和链尾进行数据共享，如下图所示：

H维度的推理时延更快，但是需要进行填充，因此在过程中，chain越长，特征图越大，冗余计算也就越多。

随着链长的增加，由于填充带来的计算开销会覆盖掉链状结构带来的增益，因此链的长度抉择十分重要，在这里作者测试了最大链长度为8。

Op_chain搜索策略

上述算法在不断连接新的算子，直到不再获得收益。ParPlan是模型的算子集合(按照推理顺序排列)，ParPlan[i]包括(𝐻 , 𝑊 , 𝐼𝐶, 𝑂𝐶, 𝐹 , 𝑆), 𝑑𝑖𝑚, 𝜌 ，其中(𝐻 , 𝑊 , 𝐼𝐶, 𝑂𝐶, 𝐹 , 𝑆) 就是论文中的ophead，分别表示算子链的头，以及头的划分维度和划分比例。

对于每一条链的头，将当前的链收益Tgain和最大收益TmaxGain初始化为0，将划分比例[ρhead-δ, ρhead+δ] 内的大收益记录在TmaxGain 。对每一个划分比例ρ 进行以下操作：

初始化chaincur为头算子，划分维度和划分比例，Tchain初始化为头的预测时间。Tnochain为不添加该算子进入链，当前链与当前算子的时间相加，而Tchain则为将算子入链之后的链推理时长。Tgain是Tchain-Tnochain ，即将算子添加到当前链的收益，收益大于Tmaxgain就更新。

当上述过程结束后，从链尾后的第一个op开始初始化为新的ophead。

CoDL架构

CoDL分为两个阶段，离线估计阶段和在线阶段：

离线阶段，CoDL设计了一个轻量级但有效的延迟预测器来指导在线阶段的操作员分区。预测器既可以实现轻量级又有效，因为 1) 它考虑了所有数据共享开销，包括数据转换、映射和同步； 2）它解析地制定了平台特征引起的非线性延迟响应，只需要为每个内核实现学习一个极其轻量级的线性回归模型来学习基本执行单元的延迟。

在线阶段由两个模块组成，即算子分区器和算子协同执行器。算子分区器的作用是为输入 DL 模型找到最佳算子分区计划，它采用混合维度划分和算子链两种技术来完成这一作用。分区器首先找到最佳分区维度（高度或输出通道）和比率（例如 0.1、0.2) ，对于每个算子作为基础计划，通过混合维度分区技术。分区器的最终分区计划是找到的链的集合，每个链运算符和链设置，即分区比率和维度。使用计划，为 GPU 和 CPU 预先安排模型权重，以避免对每个推理调用进行重新转换。

延迟预测器

在前面的介绍已经知道算子切分的开销包括：映射，前同步，推理，后同步，解映射，论文提出，相取消映射和后同步的开销是微不足道的（~ 50𝜇s）。因此，运算符协同执行的总预测延迟𝑇is如下图，其中𝑇𝑡𝑟𝑎𝑛𝑠，𝑇𝑚𝑎𝑝，𝑇𝑝𝑠-𝑛𝑐和𝑇𝑐𝑜𝑚𝑝分别表示数据转换，映射，预同步和计算的延迟。

图14（a）所示，𝑇𝑡𝑟𝑎𝑛𝑠和𝑇𝑚𝑎𝑝与数据大小有明显的线性关系，使用以数据大小为特征的线性回归来学习预测器中𝑇𝑡𝑟𝑎𝑛𝑠和𝑇𝑚𝑎𝑝的延迟。对于预同步开销𝑇𝑝𝑠-𝑛𝑐，根据我们的测量，没有明显的模式，𝑇𝑝𝑠-𝑛𝑐主要依赖于厂商的驱动实现。因此，我们在预测器中使用测量的上界（1𝑚𝑠）作为𝑇𝑝𝑠-𝑛𝑐 。

CPU和GPU的时延预测

GEMM（General Matrix Multiplication，通用矩阵乘法）和Winograd算法都是用于加速卷积神经网络（CNN）中卷积操作的计算方法。

GEMM是一种基础线性代数运算，输入数据通常会通过im2col或类似的变换被重新排列成矩阵形式，然后与滤波器权重矩阵相乘，通过使用高度优化的BLAS库（如Intel MKL、cuBLAS等）。

Winograd算法则是一种专门针对小尺寸卷积核设计的快速卷积算法。它减少了标准直接卷积所需的乘法次数，以更多的加法代替部分乘法，从而降低了整体计算复杂度，对于常见的3x3卷积核大小，Winograd可以在某些情况下提供显著的速度提升，该算法特别适合于硬件资源有限的环境，例如移动设备或嵌入式系统，在这些环境中，减少乘法操作可以带来明显的性能改进和功耗降低。

在实践中，一些深度学习库（如cuDNN）可能会根据具体情况选择最合适的算法组合来达到最佳性能。例如，在处理小型卷积核时，可能会优先考虑使用Winograd算法；而对于其他情况，则可能回退到基于GEMM的标准卷积实现。