概率论
随机变量:值取决于随机事件的结果
大写字母\(X\)表示随机变量,小写字母\(x\)表示随机变量的观测值
概率密度函数(Probability Density Function, PDF):随机变量在某个确定的取值点附近的可能性

连续 or 离散

期望:
\(p(x)\)为概率密度函数

术语
状态(state)
动作(action)
智能体(agent):动作的执行者
策略(policy, \(\pi\)):根据观测到的状态作出决策,控制智能体的运动
\(\pi:(s,a)\rarr [0,1]\)
\(\pi(a|s)=\mathbb{P}(A=a|S=s)\)

为什么要随机?博弈场景,确定的动作会让别人赢,因此policy最好是概率密度函数,action是随机抽样得到的
奖励(reward):需要自己定义,对结果影响大。强化学习目标:获得奖励总和尽可能高。
状态转移(state transition):当前状态下做一个动作,会转移到新的状态。可以是确定的,也可以是随机的(随机性从环境中来)。
状态转移函数:\(p(s'|s,a)=\mathbb{P}(S'=s'|S=s,A=a)\)
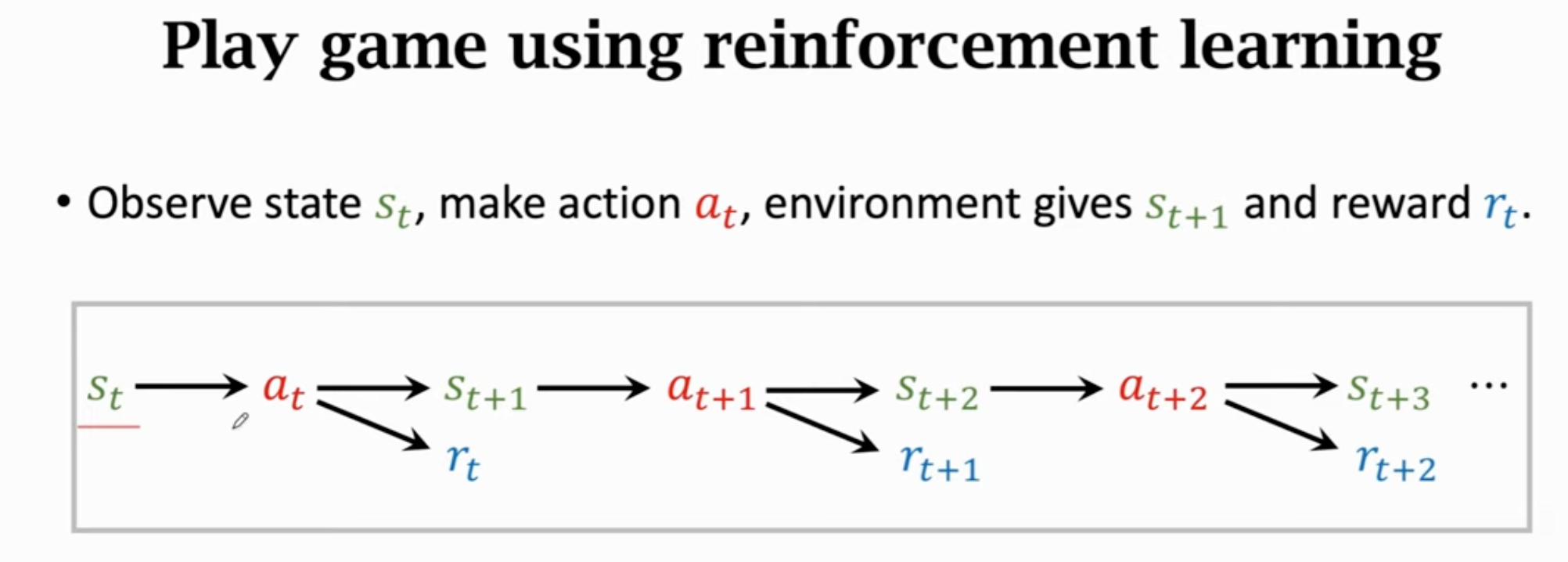
agent与环境交互:
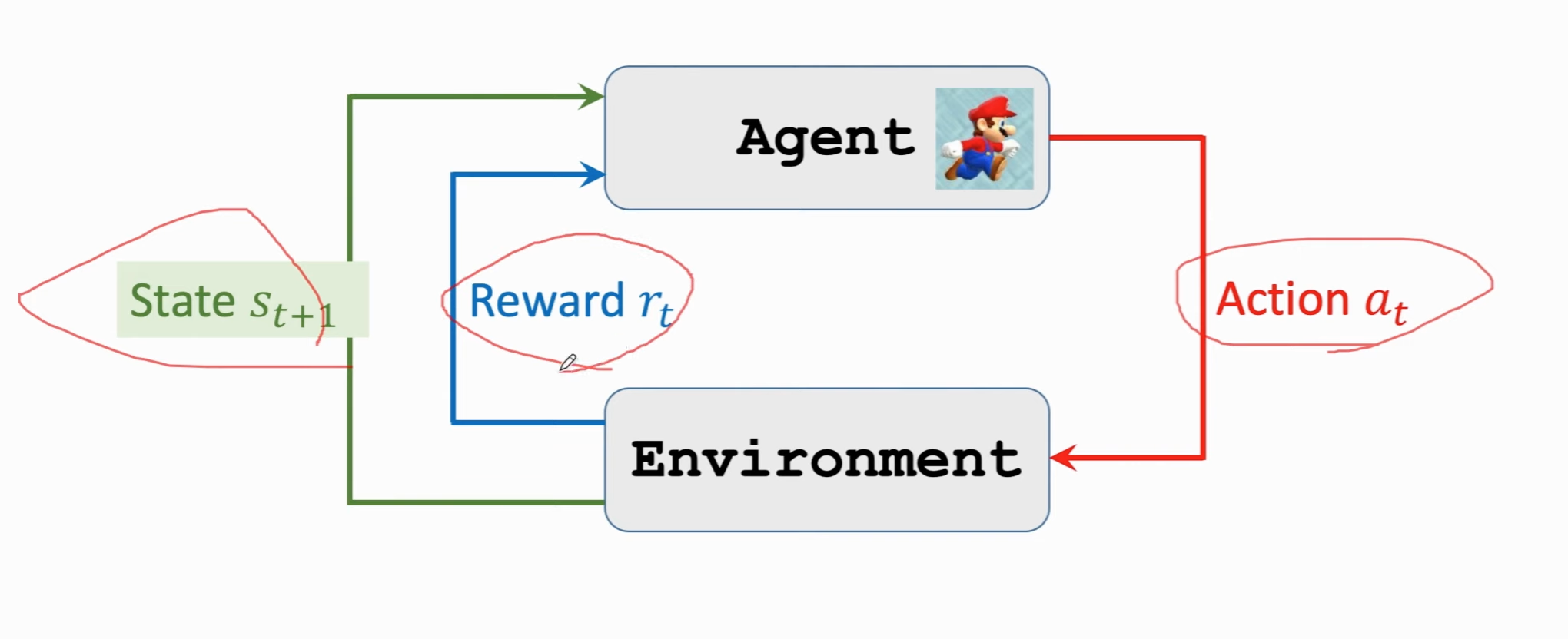
强化学习中的随机性:

通过强化学习玩游戏:

回报(return):未来的累计奖励
\(U_t=R_t+R_{t+1}+...\)
\(R_t\)和\(R_{t+1}\)同样重要吗?不
折扣回报(discounted return):\(\gamma\)为折扣率(可调节的超参数)。
\(U_t=R_t+\gamma R_{t+1}+\gamma^2 R_{t+2}+...\)
回报的随机性:假设游戏结束,奖励都观测到了,为具体的数值,则用小写字母表示;如果t时刻游戏还没有结束,奖励还没被观测到,就用大写字母\(R\)表示,折扣回报用大写字母\(U\)表示。
\(U_t\)依赖于:

动作价值函数 \(Q(s,a)\):
\(Q_{\pi}(s_t,a_t)=\mathbb{E}[U_t|S_t=s_t,A_t=a_t]\),除了\(S_t\)和\(A_t\)(观测到),未来其它的动作和状态都被积掉了;此外还依赖policy函数,可以知道对于这个policy函数,当前哪个动作好/不好

最优动作价值函数:可以对动作进行评价。

状态价值函数:判断当前状态好不好


如何用ai控制智能体?

summary