在编程和算法设计中,时间复杂度是一个至关重要的概念。它用来衡量一个算法在处理不同规模的输入数据时,执行所需要的时间增长速度。换句话说,时间复杂度能够帮助我们理解算法在面对大数据时的表现,是否能高效地完成任务。
什么是时间复杂度?
时间复杂度是一个描述算法效率的指标,通常用 O(大O符号) 来表示,它表示了输入数据规模与算法执行时间之间的关系。例如,O(n) 表示当输入数据规模为 n 时,算法的执行时间会随着 n 的增加而线性增长。
常见的时间复杂度有:
- O(1):常数时间
- O(log n):对数时间
- O(n):线性时间
- O(n log n):线性对数时间
- O(n²):二次时间
- O(2^n):指数时间
- O(n!):阶乘时间
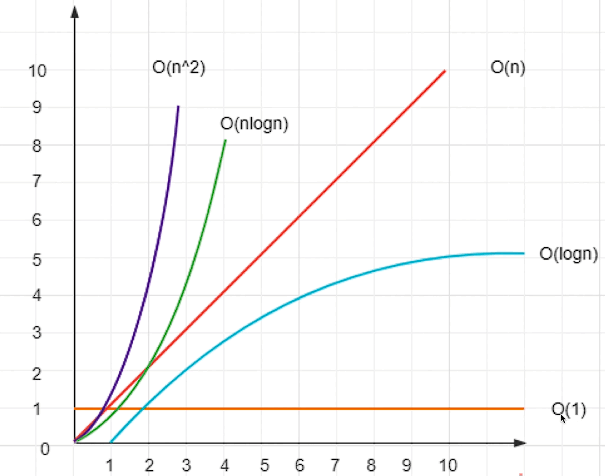
常见时间复杂度解析
1. O(1) - 常数时间
O(1) 代表常数时间复杂度,意味着无论输入数据的规模有多大,算法执行的时间都是固定的。常见的 O(1) 操作包括:
- 访问数组的某个元素
- 插入或删除链表的头节点
- 判断一个数是否为偶数或奇数
function getFirstElement(arr) {return arr[0]; // 访问数组的第一个元素,执行时间不受数组大小影响 }
2. O(log n) - 对数时间
O(log n) 表示算法的执行时间随输入规模的增大而增加的速度相对较慢。常见的对数时间复杂度算法包括 二分查找。
在二分查找中,数据集每次都会被二分,从而大幅度减少搜索的范围。随着输入数据规模 n 的增加,执行时间的增长比线性时间要慢得多。
function binarySearch(arr, target) {let low = 0, high = arr.length - 1;while (low <= high) {const mid = Math.floor((low + high) / 2);if (arr[mid] === target) {return mid;} else if (arr[mid] < target) {low = mid + 1;} else {high = mid - 1;}}return -1; }
3. O(n) - 线性时间
O(n) 表示算法的执行时间与输入数据的规模 n 成正比。常见的线性时间复杂度的操作包括遍历数组或链表等。
例如,遍历一个数组来查找某个元素,就是一个典型的线性时间复杂度操作。
function findElement(arr, target) {for (let i = 0; i < arr.length; i++) {if (arr[i] === target) {return i;}}return -1; }
4. O(n log n) - 线性对数时间
O(n log n) 通常出现在高效的排序算法中,比如 归并排序 和 快速排序。虽然它的时间复杂度比 O(n) 要高,但比 O(n²) 要低,因此常用于大规模数据的排序。
// 快速排序 function quickSort(arr) {if (arr.length <= 1) return arr;const pivot = arr[arr.length - 1];const left = [], right = [];for (let i = 0; i < arr.length - 1; i++) {if (arr[i] < pivot) left.push(arr[i]);else right.push(arr[i]);}return [...quickSort(left), pivot, ...quickSort(right)]; }
5. O(n²) - 二次时间
O(n²) 代表算法的执行时间与输入规模的平方成正比。常见的 O(n²) 算法包括 冒泡排序、选择排序 和 插入排序 等简单的排序算法。
// 冒泡排序 function bubbleSort(arr) {for (let i = 0; i < arr.length; i++) {for (let j = 0; j < arr.length - i - 1; j++) {if (arr[j] > arr[j + 1]) {[arr[j], arr[j + 1]] = [arr[j + 1], arr[j]]; // 交换 }}} }
6. O(2^n) - 指数时间
O(2^n) 表示算法的执行时间以指数形式增长,通常出现在一些递归问题中。经典的 斐波那契数列 递归算法就是一个 O(2^n) 时间复杂度的例子。
function fibonacci(n) {if (n <= 1) return n;return fibonacci(n - 1) + fibonacci(n - 2); }
7. O(n!) - 阶乘时间
O(n!) 表示算法的时间复杂度随着输入数据规模 n 的增加呈阶乘增长。典型的例子是 旅行商问题,即寻找一个最短的路径,使得每个城市都被访问一次。
// 旅行商问题的暴力解法(阶乘时间复杂度) function travelSalesman(cities) {const permutations = generatePermutations(cities);let minDistance = Infinity;for (let perm of permutations) {let distance = calculateDistance(perm);if (distance < minDistance) {minDistance = distance;}}return minDistance; }