前言
调 \(C\) 快魔怔了, 还是先来打这个
思路
方法 \(1\) : 笛卡尔树
看到这种类 \(\rm{RMQ}\) 问题直接一个笛卡尔树起手, 恰好 \(p\) 是不重的, 那么更方便了啊
搞出树树挖下性质
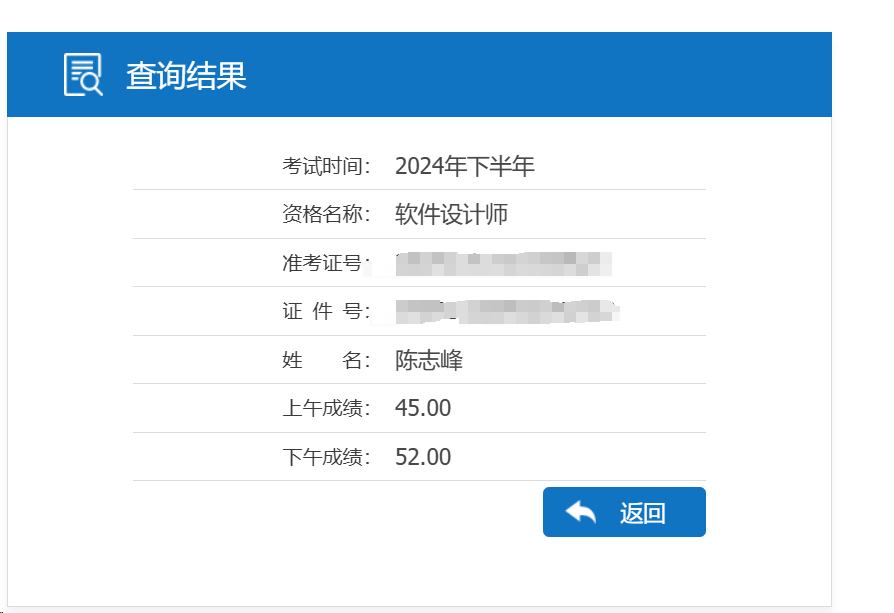
例如样例中的
4
2 4 1 3

你注意到每次删除操作相当于选择一个键值段, 然后只保留这一段的根节点, 但是这样子做不够完善, 例如这样的一个数据

你删除键值段 \(1 \sim 4\) , 那么留下的根节点 \(2\) 和一个没被删除的 \(4\) 还需要继续处理?
这种情况下应当怎么办?
我们考虑树形 \(\rm{dp}\) , 令 \(f_u\) 表示 \(u\) 子树 (柚子厨) 中的序列可能性
容易发现对于上面这种情况, 我们只需要加上 \(4\) 子树的可能性即可
我们考虑形式化的表示这些问题
令 \(f_{u, 0 / 1}\) 表示对于 \(u\) 的子树, 其中是否保留 \(u\) 的可能性数量
那么有
\[\begin{cases}
\begin{aligned}
& f_{u, 1} \gets \sum_{k = 0}^{1} f_{ls, k} \cdot \sum_{k = 0}^{1} f_{rs, k}\\
& f_{u, 0} \gets \left[ \exists fa_r \right] \cdot \sum_{k = 0}^{1} f_{ls, k} + \left[ \exists fa_l \right] \cdot \sum_{k = 0}^{1} f_{rs, k}
\end{aligned}
\end{cases}
\]
简化一下, 去掉 \(0, 1\) 维
\[\begin{cases}
\begin{aligned}
& f_{u} \gets f_{ls} \cdot f_{rs}\\
& f_{u} \gets \left[ \exists fa_r \right] \cdot f_{ls} + \left[ \exists fa_l \right] \cdot f_{rs}
\end{aligned}
\end{cases}
\]
这种代码就不写了, 并不困难
方法 \(2\) : 朴素 \(\rm{dp}\)
这种方法应该好想一点
你发现一个可以通过操作 \([l, r]\) 来保留两端的点, 仅有这两种可能:
- \(a_l\) 为 \([l, r]\) 区间中最小值
- \(a_r\) 为 \([l, r]\) 区间中最小值
简单分讨即可, 具体见 Luogu 题解
总结
笛卡尔树上常见的树形 \(\rm{dp}\)