Codeforces 1842I. Tenzing and Necklace-编程知识

Codeforces 1842I. Tenzing and Necklace

news/2024/12/23 22:26:30/文章来源:https://www.cnblogs.com/DeaphetS/p/18625185

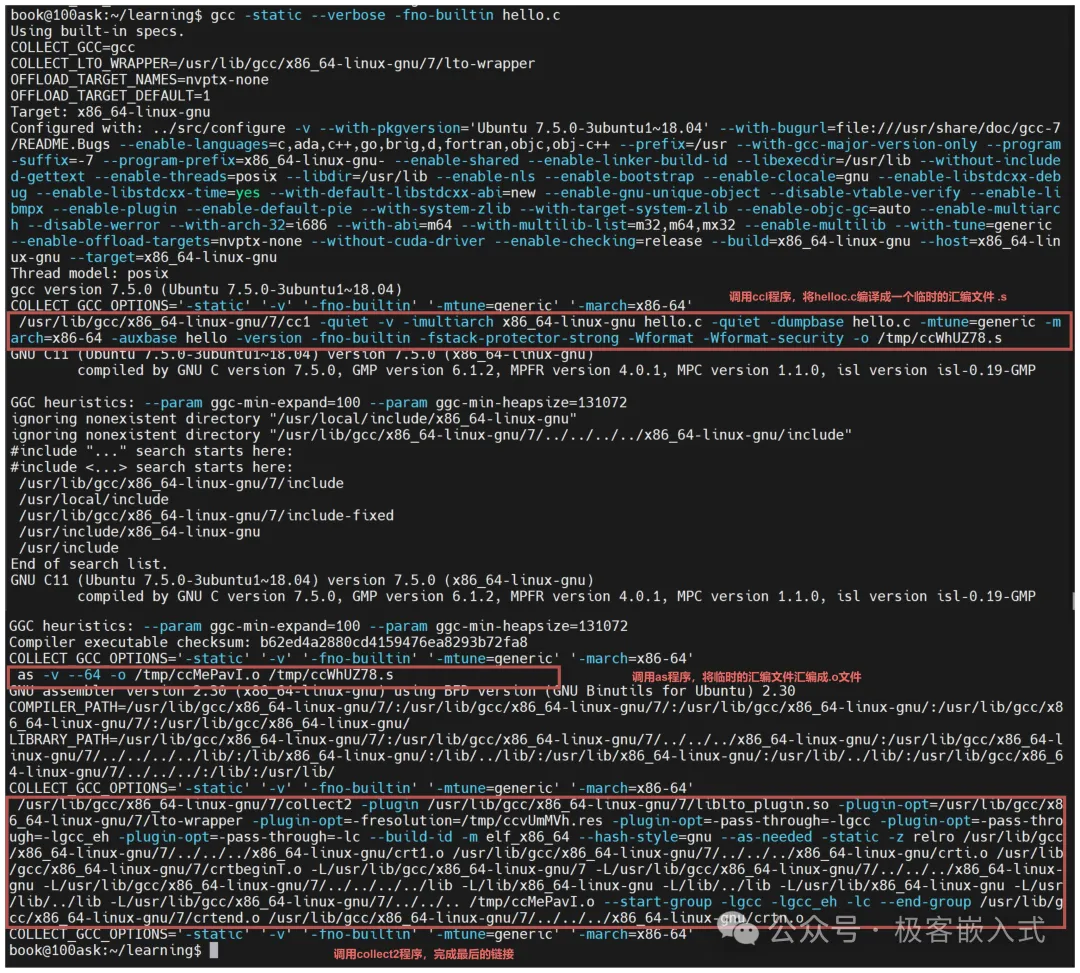
神仙题。本题解参考官方题解进行编写，并补充了最后比较关键的怎么调整 $m$。

题目链接：I - Tenzing and Necklace

题目大意：给定一个环，环上有 $n$ 个点与 $n$ 条边，第 $i$ 条边连接 $i$ 与 $i\bmod n +1$，边权为 $a_i$。要求断开若干边使得环断为若干段，并且每一段上点的个数不超过 $k$，求断开边权和的最小值。

开场的三个结论

首先钦定必须断开 $m$ 条边，并设 $S_i$ 表示，在环上断开的编号最小的边的编号为 $i$ 时，花费最小的断边编号序列（编号从小到大排列）。官方题解采用了较大篇幅描述了以下三点：

设 $x\lt y$，令 $A=S_x,B=S_y$。可以通过只对 $B_2,B_3,\dots,B_m$ 进行调整，使得对 $\forall 1\le i\le m$，均能满足 $A_i\le B_i$，且调整前后对应的花费不变。同理，也可以通过只对 $A_2,A_3,\dots,A_m$ 进行调整使其满足对应条件；
在 $A,B$ 满足 $A_i\le B_i$ 的基础上，可以进一步只对 $B_2,B_3,\dots,B_m$ 进行调整，使得对 $\forall 1\le i\lt m$，均能满足 $A_i\le B_i\le A_{i+1}$。同理，也可以通过只对 $A_2,A_3,\dots,A_m$ 进行调整使其满足对应条件；
对任意 $y\gt A_2$，一定有 $S_{A_2}$ 对应的花费不比 $S_y$ 大。

前三个结论的证明

这几个结论的详细证明可参考官方题解，这里提供几个配图进行辅助说明，不感兴趣可以跳过。

结论一

设 $x\lt y$，令 $A=S_x,B=S_y$。可以通过只对 $B_2,B_3,\dots,B_m$ 进行调整，使得对 $\forall 1\le i\le m$，均能满足 $A_i\le B_i$，且调整前后对应的花费不变。同理，也可以通过只对 $A_2,A_3,\dots,A_m$ 进行调整使其满足对应条件。

取环上的某一段进行说明，若此时存在 $A_i\gt B_i$，考虑之后的第一个位置 $j$ 使得 $A_j\le B_j$。注意到由于是在环上，所以一定存在这样的情况（最坏情况是回到开头，$j=m+1$）。

我们把这种情况画出来，如图所示，红色代表方案 $A$ 选取的断点，蓝色代表方案 $B$ 选取的断点，显然同色点之间的距离是符合题目要求的。

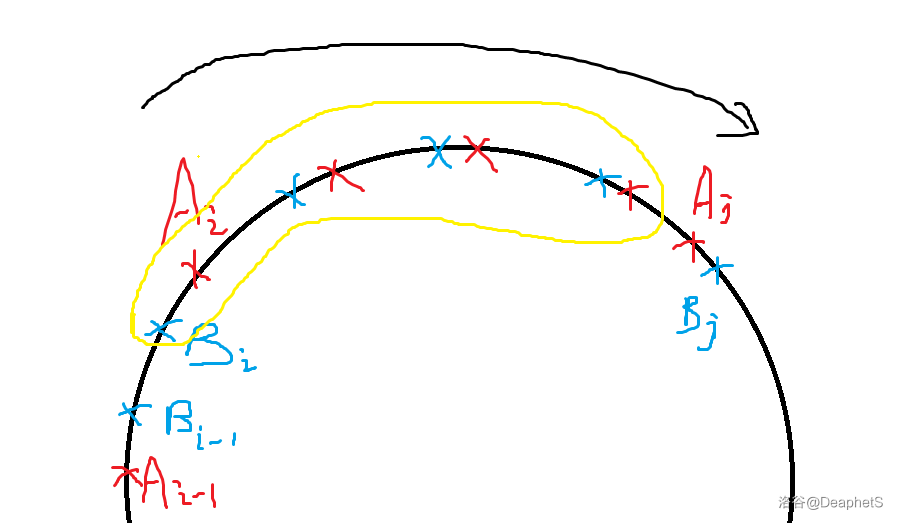
这时我们发现，把黄色部分的每对红蓝点进行对调，是依旧能符合同色点之间的距离要求的。而把所有蓝色点都变到对应红色点的位置上，正好能符合 $A_i\le B_i$ 的要求。

在对应的花费上，由于 $A,B$ 分别代表着各自起始位置的最优解，所以在调整之后的花费肯定不能比原来的更少（无论是红 $\to $ 蓝还是蓝 $\to$ 红）。所以黄色区间内红色点权值和一定和蓝色点权值和相同，因此能满足花费不变的条件。

结论二

在 $A,B$ 满足 $A_i\le B_i$ 的基础上，可以进一步只对 $B_2,B_3,\dots,B_m$ 进行调整，使得对 $\forall 1\le i\lt m$，均能满足 $A_i\le B_i\le A_{i+1}$。同理，也可以通过只对 $A_2,A_3,\dots,A_m$ 进行调整使其满足对应条件。这里假设 $A_1\lt B_1\le A_2$。

同样考虑第一次出现 $B_i\ge A_{i+1}$ 的位置，同理一定存在 $B_j\lt A_{j+1}$。

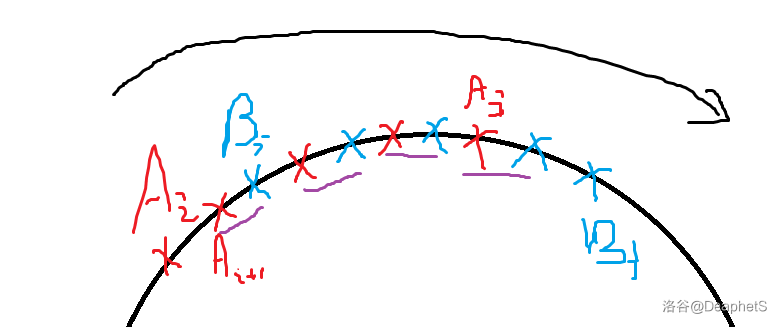
原理和结论一的证明类似，可以发现将紫色线画出的几对红蓝点进行一一互换能保证满足条件。

结论三

对任意 $y\gt A_2$，一定有 $S_{A_2}$ 对应的花费不比 $S_y$ 大。

找到最小的 $i$ 满足 $B_i\le A_{i+1}$，如图所示。

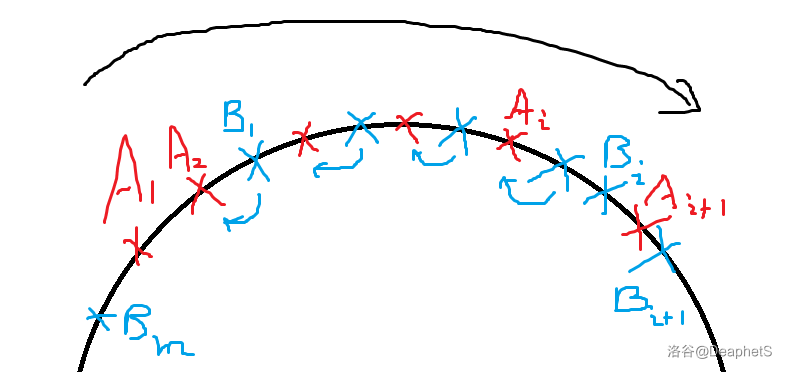
按照箭头所示将蓝色断点全部移动到对应位置，即可完成调整。由于 $A$ 是一个固定 $A_1$ 为开头的最优解，所以若将红点变成对应蓝点（此时红色点间距离一定满足限制），对应花费一定不会减少。因此完成蓝 $\to$ 红的转化后花费一定不会变大。

找出某个 $m$ 对应的最优解

以上几点实际上证明了这么一件事情，当我们需要求某个 $S_y$ 的时候，若此时我们已经拥有 $x,z$ 使得 $x\lt y\lt z$ 且 $S_x$ 与 $S_z$ 均已被求出，那么可以保证一定存在对应的最优解使得：对 $\forall 1\le i\le m$，有 $S_x(i)\le S_y(i)\le S_z(i)$。这里 $S_x(i)$ 表示编号序列 $S_x$ 的第 $i$ 个元素。于是我们可以考虑分治求解。

具体的，我们先在原问题上找到必须断开第 $0$ 条边（也就是第 $n$ 条边）的最优解（不限制断开的边数）。这个可以看成一个在序列上的问题，可以使用单调队列维护 DP 轻松求出，我们称这个解对应的断边编号序列为原始解 $A$，并令 $m=|A|$。（这里注意，这个 $m$ 其实并不是我们钦定的，而是我们求出来的）

根据之前的结论，一定存在一个最优解 $B$ 使得 $A_i\le B_i\le A_{i+1}$ 恒成立，所以可以在此基础上进行分治。

令 $Sol([L_1,R_1],[L_2,R_2],\dots,[L_m,R_m])$ 表示当前需要求出符合条件 $B_i\in [L_i,R_i]$ 的最优解 $B$，一开始 $L_i=A_{i-1},R_i=A_i$，特别的我们令 $L_1=1$。

在求解时，我们可以先令 $b_1=\lfloor\frac{L_1+R_1}{2}\rfloor$，然后使用朴素的线性 DP 求出符合限制条件的一组解 $b$，并且可以递归计算 $Sol([L_1,b_1),[L_2,b_2],\dots,[L_m,b_m])$ 与 $Sol((b_1,R_1],[b_2,R_2],\dots,[b_m,R_m])$。这样最多递归 $\log$ 层，每层都可以合计在 $O(n)$ 的时间复杂度内求解，于是可以做到 $O(n\log n)$ 的一次对 $m=|A|$ 的求解。

对于 $m$ 为其他值的情况

官方题解对这种情况的说明较为简略，我们分两部分说明。

全局最优解的序列长度调整

设我们一开始求出的原始解为 $A$，最终的最优解为 $B$，其中 $|A|=m,|m-|B||\ge 2$，不妨设 $m\gt |B|$。

考虑第一个出现 $B_i\ge A_{i+1}$ 的位置，如图所示，由于 $m-|B|\ge 2$ 一定会出现这样的情况。注意到由于 $A$ 和 $B$ 分别是某特定条件下的最优解，所以图中一定不会出现连续三个及以上的同色点，否则完全可以做到删去中间的那个断点使得在满足题目限制的情况下花费变少，产生矛盾。

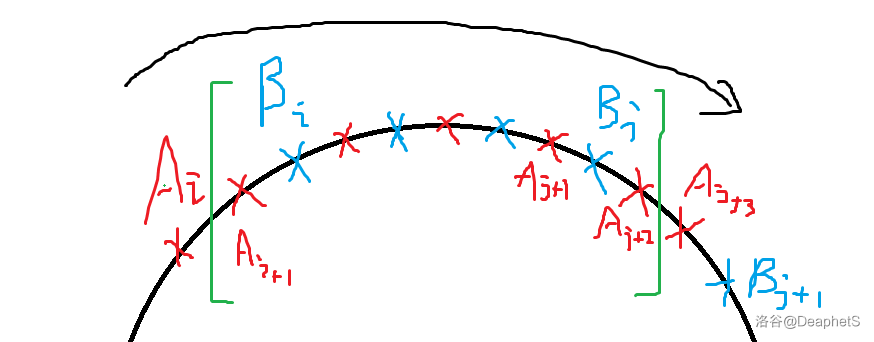
此时对上图中绿色区间内的红蓝点集合进行对调，首先还是和之前的证明思路一样，对调后同色点间的距离仍然满足条件，且花费不会产生变化，所以可以通过一次调整使得最优解的序列长度 $+1$，于是在不断的调整过后可以让 $B$ 的长度变为 $m-1$。对于 $|B|\gt m$ 的情况也可以使用类似的调整，于是一定存在 $m'$ 使得存在断点序列长度为 $m'$ 且 $|m-m'|=1$ 的全局最优解。

找到断边个数为 $m-1$ 或 $m+1$ 的最优解

于是我们只需要分别找到断边个数为 $m-1$ 和 $m+1$ 的最优解即可。但问题是在求这个最优解之前我们需要先找到一个固定开头且固定断边条数为对应值时的最优解。

这个问题看上去可以采用 wqs 二分的思想做，即给所有边钦定一个固定的增量，按照之前我们求原始解的方式去求出一个对应条件下的最优解，并判断边条数是否满足要求，在此基础上进行二分。但这题存在一个致命的问题，就是不一定存在断边条数恰好符合要求的增量，比如样例一。

不过貌似是存在某种很牛的调整法求出对应初始解的，且 MagicalFlower 应该是采用的这种做法，感兴趣的大佬可自行了解。

下面介绍另一种做法。

对于 $m+1$ 的情况是比较好做的，对于原始解跑一遍 $Sol([0,0],[L_1,R_1],[L_2,R_2],\dots,[L_m,R_m])$ 即可求出一个断边条数为 $m+1$ 的初始解 $b_0\sim b_m$。这是因为若存在 $b_i\notin [L_i,R_i]$，那么根据抽屉原理，一定存在某个区间 $[L_j,R_j]$ 内有两个断点，就会出现如图所示的情况。

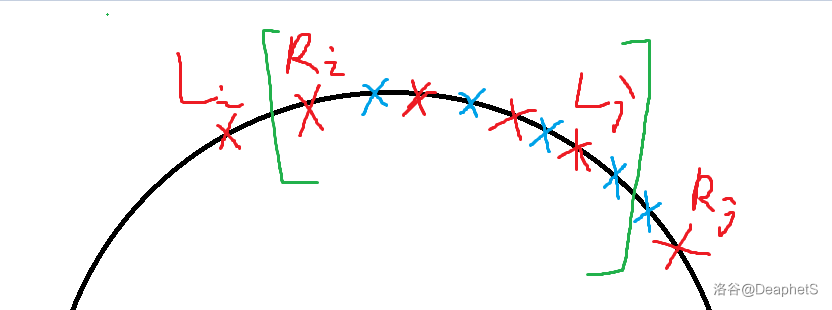
那么对绿色范围内的点进行调整即可做到让蓝点均落在对应红点的区域内。

对于 $m-1$ 的情况，当然首先要判一下断边数量是否可以再减少，这一判断是平凡的，之后跑一遍 $Sol([0,0],[L_2,R_2],[L_3,R_3],\dots,[L_{m-1},R_{m-1}])$ 即可求出一组初始解 $b_1\sim b_{m-1}$，其中 $b_1=0$。这时我们把 $[R_{m-1},L_2]$ 看成一个额外的区间（这个区间跨过了 $0$ 点），这样也是共 $m-1$ 个区间。同样的，若出现了 $b_i\notin [L_i,R_i]$ 的情况，依旧会出现某个区间内有两个断点，采用相同的方式调整即可。

在求出两种情况的初始解后，再次采用之前分治的处理方式即可求出断边个数为 $m-1$ 和 $m+1$ 的最优解，比较一下即可得到全局最优解。