密码学基础
哈希算法
哈希算法是指把任意输入值通过特定方式(hash 函数)处理后生成一个结果值。有时会发生输入值不同,但是处理后结果值相同的情况,这就叫哈希冲突。但一般来说,只要哈希函数设计得当,并且样本足够大,那么发生哈希冲突的概率可以忽略不计。因此,可以认为任意值通经过哈希函数处理后得到结果值都是唯一的。
对称加密和非对称加密
未经任何加密处理的数据称为明文,对明文以某种算法加密后就变成密文。密钥是一种参数,它是在明文转换为密文或将密文转换为明文的算法中输入的参数。
密钥分为对称密钥与非对称密钥,分别应用在对称加密和非对称加密:
- 对称加密:使用同一个密钥去加密和解密数据
- 非对称加密:使用公钥加密数据,使用私钥解密数据,公钥是公开的,私钥则是私有的
数据结构基础
哈希指针
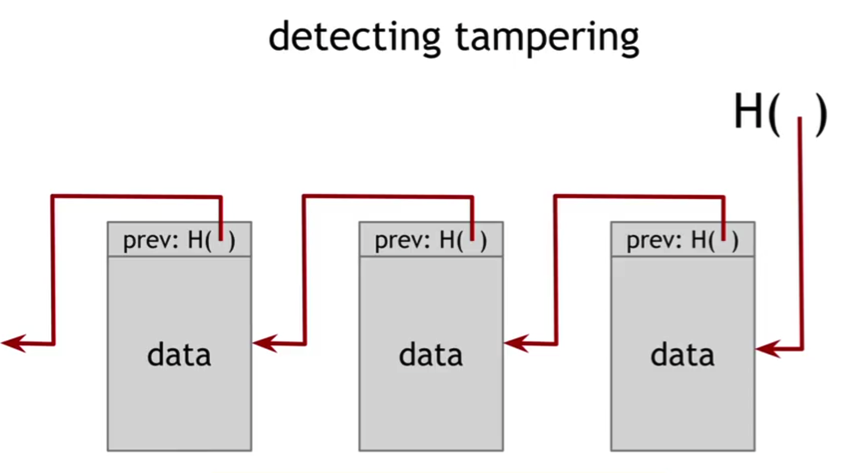
链式存取的数据结构,链表中的数据以节点来表示,每个结点由元素和指针构成。区块链和普通链表相比,使用哈希指针取代普通指针。所谓哈希指针,其实是一个哈希值,由上一个节点的内容经由某个哈希函数计算得出。
哈希指针是为了检测某一节点可能发生的修改,因为某一节点被修改,就意味着指向其的哈希指针将对不上。用户手持最新的哈希指针,开始回溯,只要发现某一个节点哈希指针对不上,即可找出被修改的节点。
实际应用中,在全节点会保存所有区块的 kv 值,其中 key 是该区块的哈希值,value 是区块信息,轻节点根据持有的哈希指针询问全节点,即可得到整条区块链的信息
默克尔树
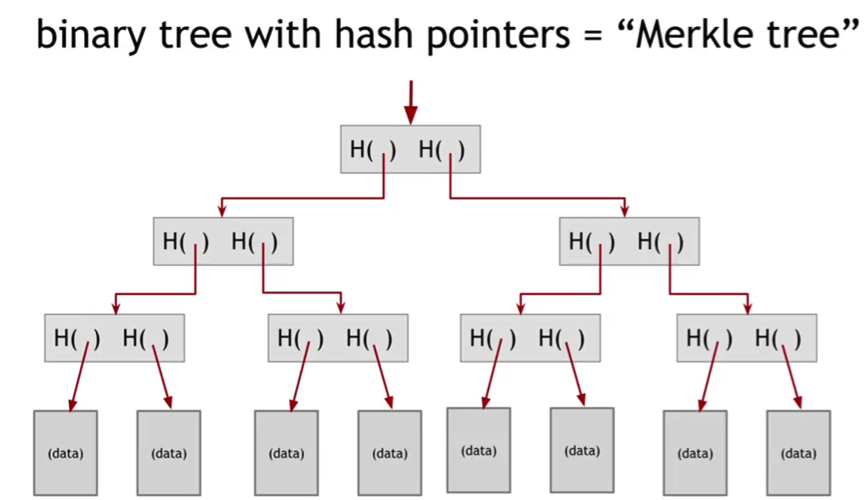
默克尔树与二叉树的区别是使用哈希指针代替普通指针。最底层的是数据块,上层则是哈希指针。由图可知,由数据块计算得出的哈希指针存储在其父节点,而再往上,每两个哈希指针共同计算得出的哈希指针则存储在其父节点。
因为二叉树的性质,默克尔树的查找效率更高。
协议
现实生活中,使用现金交易,现金具有唯一性,从 A 转移到 B,A 失去现金,B 得到现金。
后来有了数字货币,数字货币与现金用处一样,从 A 转移到 B,A 的账户扣除,B 的账户增加。但数字货币容易伪造,因此,每一笔交易都必须被记录,例如由央行记录,也就是账本,A 转账给 B 100 币,这笔交易被央行记录,那么交易有效。但这种方式问题在于,类似央行的中心化机构权力太大,完全可以凭空捏造交易记录。
区块链的目的是去中心化管理交易记录,或者说数据,因此区块链是一个去中心化的数据存储模型。还是上述的例子,原本由央行管理的账本,现在由所有人共同管理,每个人都独立保存一个账本,一个交易记录是否能记录到账本,需要所有人共同表决。具体实现上,账本的数据模型为区块链,每一笔交易记录是一个区块,如果合法则添加到链表。
为了确保区块链正常运作,必须遵守以下协议
1. 币的来源
区块必须指明币的来源,假设 A 转账 B,转账方是 A,那么需要 A 指明币的来源,即 A 上一次作为收款方的区块,以便通过回溯验证该笔交易正确性。
2. 签名
参与区块链运作的每个成员都拥有一对公私钥,对公钥哈希的结果值就是标识该成员的“地址”。在一个区块中包含转账方的地址,以及转账方对地址使用私钥加密的“签名”。其他成员可以使用转账方公开的公钥对该区块的签名解密,如果解密结果与地址吻合,则认为交易不是他人伪造,确实由转账方发起。
3. 铸币权
并不是每个成员都有权力将区块加入区块链,只有获得铸币权的成员才有该权力。区块的头部 + 某个随机数 通过某个哈希函数可以算出某个哈希值,该哈希值只有小于设定的难度值,才允许加入区块链。成员构建一个自身认为合法的区块,要想加入区块链,必须不断的尝试随机数,只有算出满足条件的随机数才能将其加入区块链,也就是获得铸币权,作为奖励,该成员会获得一定数额的虚拟币。其他成员则需要验证该区块是否符合难度要求,以及是否合法,只有通过才会将其记录下来。
实现
UTXO
在区块链上,账本记录的都是交易记录,如果要计算个人余额,就需要用到 UTXO 模型,全称 Unspent Transaction Output,直译即未花费交易输出。每笔比特币交易都有输入和输出,一方支付的币是“交易输入”,另一方收到的币是“交易输出”,“交易输出”又可以在其他交易作为“交易输入”,此时便会抵消掉部分金额。UTXO 模型记录了所有“交易输入”和“交易输出”,由此可以计算个人余额
手续费
为了避免拥有铸币权的节点自私,只记录自己的区块,每一个区块加入区块链,都需要支付一定的手续费
计算目标值
获取铸币权,也即使“挖矿”,需要不断的计算符合条件的随机数,使得区块计算出的哈希值符合难度条件,但有时候即使把所有随机数遍历也无法获得目标值,所以需要引入新的计算变量。每一个节点都有一个默克尔树,可以对默克尔的创世节点的“指向前一个区块指针”区域赋随机值,从而扩大整个区块的计算范围
比特币总量
币的产出主要依靠矿工获得铸币权,但当币的总量到达一定数目时,矿工可获得的币就会减半,比如最开始挖到一个区块奖励 50 币,当币的总量到达 20w 时,奖励就会减半,所以币的产出会越来越少,最终达到一个临界值
等待确认
假设 A 节点发布了 A-B 的区块,A 节点含有恶意,又试图发布 A-A 的区块,将已经花费的币转回自身,那么其他诚实节点会识别并拒绝加入,但如果这两个区块同时发布,那么区块链就会形成分支,最终最长的分支将胜出,从而形成双重消费攻击。为了防止该问题,一个区块必须等待后续几个区块的确认才会最终被接纳,有时候不需要确认,因为大多数节点是诚实的,恶意节点的区块大概率不会被接纳
区块链网络
区块链基于 P2P 网络,通过 TCP 实现各个节点的通信。每一个节点收到一个交易消息就会转发给邻居节点,下一次收到同样的消息就不需要重复发送。节点的邻居节点不依赖底层的拓扑结构,完全随机选取。基于上述的实现,区块链的性能并不高,其特点是简单,健壮。节点会监听交易池的交易消息,如果将某一消息加入区块,那么就需要将该消息从池中删除,并将其他冲突交易删除
挖矿
所谓挖矿,就是算区块头部的哈希值,要求小于给定的目标值。目标值越大,哈希值取值范围越大,挖矿难度越小,反过来目标值越小,哈希值取值范围越小,挖矿难度越大。
挖矿难度的直接体现就是出块时间,出块时间需要维持一个恒定值,不能太快也不能太慢。太快会导致分支过多,容易被恶意节点攻击,太慢则会影响性能。因此挖矿难度,也就是目标值必须根据实际情况动态调整,使其维持恒定。比特币规定平均区块为 10 分钟,每 2016 个区块调整一次,因此调整公式为:target = target * (actual time) / expected time,expected time 是挖到第 2016 个区块期望的时间,即 2016 * 10,actual time 是挖到第 2016 个区块需要的时间,由此可见当实际时间大于期望时间,目标值会增大,反之则减小。实际上,目标值的调整是有区间的,最多不能超过四倍。
具体实现上,调整难度由代码控制,每个节点到 2016 个区块就会自行调整。如果有恶意节点不调整,那么区块头的难度系数与其他节点不一致,其他诚实节点不会承受它发布的区块。
为了提高挖矿效率,出现了一种名为矿池的组织,即组建一个矿机集群,角色分矿主和矿工。矿工负责计算,矿主负责组装区块并发布,获得效益再分发给矿工。由于挖矿的随机性,为了公平分配收益,规定矿工只要挖到符合难度要求区域的值即可提交矿主,哪怕并不符合条件,当挖到符合条件的区块时,再根据每个矿工的出力多少分配收益
比特币脚本
一次交易中,转账方所花费的币来源于上一次其作为收款方收到的币,因此,对于同一个账户,上一次交易的输出与下一次交易的输入必须作校验,该目的由比特币脚本实现。输出脚本与输入脚本进行匹配,结果为真,才允许使用这一笔钱。输出脚本可以理解为对输出的币上锁,而输入脚本则对币解锁以获得使用权。一般先执行输入脚本,再执行输出脚本,使用栈来存储指令
1. P2PK(Pay to Public Key)
input scriptPUSHDATA(Sig)
output scriptPUSHDATA(PubKey)CHECKSIG
执行顺序如下:
PUSHDATA(Sig) # 将输入方公钥签名压栈
PUSHDATA(PubKey) # 将输入方公钥压栈
CHECKSIG # 弹出栈顶两个元素,检查公钥签名正确
2. P2PKH(Pay to Public Key Hash)
这种方式与 P2PK 不同在于对 PubKey 使用 Hash 处理,起到隐藏地址的作用
input scriptPUSHDATA(Sig)PUSHDATA(PubKey)
output scriptDUPHASH160PUSHDATA(PubKeyHash)EQUALVERIFYCHECKSIG
执行顺序如下:
PUSHDATA(Sig) # 将输入方公钥签名压栈
PUSHDATA(PubKey) # 将输入方公钥压栈
DUP # 复制栈顶元素并压栈
HASH160 # 弹出栈顶元素并 HASH,再压入栈
PUSHDATA(PubKeyHash) # 将输入方公钥HASH压栈
EQUALVERIFY # 比较栈顶两个元素,相同则从栈删除
CHECKSIG # 弹出栈顶两个元素,检查公钥签名正确
3. P2SH(Pay to Script Hash)
input script...PUSHDATA(Sig)...PUSHDATA(Serialized RedeemScript)output scriptHASH160PUSHDATA(RedeemScriptHash)EQUAL
输入脚本给出签名以及序列化的 RedeemScript,与输出脚本的哈希值匹配,匹配则反序列化执行 RedeemScript,验证输入脚本的签名是否正确,RedeemScript 的形式可以是 P2PK、P2PKH、多重签名形式
4. 多重签名
有时候要求一个输出必须要有多个签名才能使用,比如五个签名只要匹配三个就能使用
最早的多重签名如下,输入脚本提供 M 个公钥,只要在输出脚本提供的 N 个公钥中符合 M 个,即通过验证,注意相对顺序要保持一致
input scriptfalse # 为了解决最初多重签名设计BUG,无意义PUSHDATA(Sig_1)PUSHDATA(Sig_2)...PUSHDATA(Sig_M)output scriptMPUSHDATA(PubKey_1)PUSHDATA(PubKey_2)...PUSHDATA(PubKey_N)NCHECKMULTISIG
这样做的坏处是输出方和输入方对验证签名数量续协商一致,不同的平台也许会有不同的规则,一般配合 P2SH 使用,把多重签名放在 RedeemScript,由输入方提供 RedeemScript,输出方提供 RedeemScriptHash,不需要知道规则细节
5. Proof of Burn
这种形式的 output script 只有一条 RETURN 指令,无论后面是否还有其他指令都不会执行,直接返回 FALSE,也就是说该 output 永远花不出去,应用场景有两种:一是销毁该输出的币,二是利用区块链的不可篡改性质 保存数据,coinbase 域也能实现保存数据的目的,但只有拥有记账权的节点才能操作 coinbase
outputRETURN...
区块链分叉
区块链中出现分叉的原因有三种:
- 拥有记账权的节点同时插入各自的区块
- 恶意节点人为插入恶意区块制造分叉
- 节点之间的协议不一致,这种造成的分叉又分硬分叉和软分叉
假如协议更新,区块的限制大小由 1M 变为 4M,大多数节点接受,小部分节点拒绝,那么当出现大于 1M 的区块时,大多数节点将其加入区块链,小部分节点视为非法区块拒绝加入,继续接收其他区块,此时就会出现分叉,不同协议的节点都沿着各自的分叉继续延伸,并且只认为自己的链条才是最长合法链,这就是硬分叉
还是上述的例子,区块的限制大小由 1M 变为 0.5M,部分节点接受,部分节点不接受,那么当出现小于 0.5M 的区块时,所有节点接受,当出现大于 0.5M 小于 1M 的节点时,接受新协议的节点拒绝,不接受新协议的节点接受。此时称接受新协议的节点为新节点,不接受新协议的节点为旧节点,旧区块(大于 0.5M 小于 1M)不被新节点认可,出现分叉,新区块(小于 0.5M)则被所有节点认可。如果新节点算力更强,久而久之,只有旧区块的链将会作废,意味着旧节点白费力气了。软分叉出现的分叉只是临时的,最终还是会回到一条链,但也有可能还会出现分叉
区块链匿名性
区块链的匿名性主要体现在隐藏了用户的身份信息,对外只提供一个地址。但区块链的交易是公开的,意味着所有人都可以查看交易记录,每个交易都会有对应的输入地址和输出地址,即可进行追溯到对应的源头,根据交易记录有一定概率推倒出用户信息。另外,当比特币与现实世界发生交互时,如买币卖币,一样会暴露用户身份
基于上述问题,一来可以采用代理的方法隐藏真实身份,二来可以采用混币的方法,通过将用户的加密货币与其他用户的加密货币进行混合,使得交易路径变得模糊不清,从而保护用户的交易隐私和安全性
由此可见,区块链在隐私保护方面并不是完全安全的,可以采用零知识证明加强隐私保护
零知识证明是指:证明方向验证方证明一个陈述是正确的,而无需透露“该陈述是正确的”以外的其他信息。比如,张三持有两个值 x=1 和 y=6,张三要向李四证明 x+y=7,但张三不能告诉李四 x=1 和 y=6
要想实现零知识证明,需要用到同态隐藏的三个性质:
-
如果 x,y 不同,那么它们的加密函数值 E(x) 和E (y) 也不相同
-
给定 E(x) 的值,很难反推出 x 的值
-
给定 E(x) 和 E(y) 的值,可以很容易地计算出某些关于 x,y 的加密函数值
﹣ 同态加法:通过 E(x) 和 E(y) 计算出 E(x+y) 的值
﹣ 同态乘法:通过 E(x) 和 E(y) 计算出 E(xy) 的值
﹣ 扩展到多项式
根据上述三个性质,回到上面的例子,我们可以按下面步骤实现零知识证明:
- 张三把 E(x) 和 E(y) 的值发给李四
- 李四计算 E(x) + E(y) 的值,并得到 E(x) + E(y) = E(x+y),此处利用了性质三
- 李四计算 E(7) 的值,如果 E(x) + E(y) = E(x+y) = E(7),那么也有 x+y = 7,但李四并不知道 x 和 y 的具体值
常规的区块链交易,当资产从一方发送到另一方时,该交易的详细信息对网络中每一方都可见。基于零知识证明的交易,其他人只知道发生了有效的交易,而不知道发送方、接收方、资产类别和数量,花费的身份和金额可以隐藏起来,起到隐私保护的作用
以太坊概述
以太坊(Ethereum)是一个开源的公共区块链平台,其专用加密货币称为以太币(Ether),相比传统区块链应用,以太坊有以下三个特点:
- 更快的出块速度
- 使用权益证明代替工作量证明
- 提供智能合约
以太坊账户
过去使用比特币,要想知道余额,必须根据 UTXO 计算。以太坊提供了账户的概念,由全节点统一维护各个节点的账户。有了账户,每次交易不需要给出加密货币的输入和输出地址,也不需要将多余的输出分给自己的另一个地址,只需要操作账户余额即可。账户的存在对双重开销攻击具有天然的防范性,但无法对付重放攻击(收款方重新发布该次交易,使得转账方再次支出余额),为此以太坊为每个账户设置了一个计数器,每次交易发布会带有本次交易是第几次的标记,对应的账户计数器则递增,如果出现重复次数的交易则视为非法交易
以太坊数据结构
1. 状态树
以太坊使用状态树(MPT)的数据结构实现账户地址到账户的映射,状态树基于字典树的存储和组织形式实现,由四种类型的节点组成:扩展节点(Extension Node)、分支节点(Branch Node)、叶子节点(Leaf Node)和空节点
扩展节点只能有一个子节点,分支节点可以有多个子节点,叶子节点没有子节点。 扩展节点和叶子节点中存储 Key/Value 值,Key 通常是一个账户或者是一个合约的地址,以太坊使用 RPL 对 Key 进行编码。Value 是以太坊中的账户状态(包括账户余额、合约代码、存储数据等),经过 RPL 编码后存储
每次发布新的区块,状态树的部分节点会发生变化,这些改变不是在原地改,而是新建分支,保留原来的状态。具体来说,当一个新的区块生成时,它包含了一系列的交易记录,这些交易可能会影响到状态树中的多个节点。为了更新状态树,以太坊系统会执行以下步骤:
- 复制状态树:系统会复制当前的状态树,得到一个副本
- 应用交易:系统会逐个应用新区块中包含的交易,对于每个交易,系统会根据其操作(如转账、合约创建、合约调用等)修改副本状态树中相应的节点
- 生成新树: 当所有交易都被处理完毕后,系统会得到一个更新后的状态树,这个更新后的状态树就反映了新区块产生后账户状态的变化
通过这种方式,状态树的变化并不是在原地进行修改,而是通过复制当前状态树,应用交易并生成新的状态树来实现的。原来的状态树会被保留下来,以便在需要时进行查询和验证。这种设计保证了以太坊的安全性和可靠性,同时也使得历史状态的追溯和审计成为可能
2. 交易树
交易树是以太坊中存储交易信息的数据结构,每个区块包含了一组交易,这些交易会被存储在交易树中。交易树的根节点的哈希值被包含在区块头中,从而保证了交易的完整性和不可篡改性
交易树的结构类似于 Merkle 树,它由多个节点组成,每个节点包含了对应的交易信息的哈希值。通过对所有交易信息进行哈希计算,并按照一定规则构建树结构,最终形成了一个树状的数据结构。这样,只需存储根节点的哈希值,就可以验证整个交易列表的完整性
3. 收据树
收据树是以太坊中存储交易执行结果的数据结构,每个交易在执行后会产生一个收据(Receipt),其中包含了执行状态、日志和消耗的 Gas 等信息。这些收据会被存储在收据树中,而收据树的根节点的哈希值也被包含在区块头中
收据树的结构与交易树类似,也是一个基于 Merkle 树的数据结构,每个节点包含了对应的收据信息的哈希值。通过对所有收据信息进行哈希计算,并按照一定规则构建树结构,最终形成了一个树状的数据结构。这样,只需存储收据树的根节点的哈希值,就可以验证整个收据列表的完整性
4. 布隆过滤器
在以太坊中,有时需要执行一些复杂的查询操作,比如查询过去某段时间内与某个智能合约相关的交易。如果遍历整个区块链则效率太低,为了提高查询效率,引入了布隆过滤器。布隆过滤器是一种空间效率高且可以快速判断一个元素是否存在于集合中的数据结构,布隆过滤器判断不存在的元素一定不存在,判断存在的元素有可能不存在。在以太坊中,每个区块都有一个包含自身所有交易的布隆过滤器,执行查询操作时,使用布隆过滤器快速判断某个交易是否可能与该区块相关,然后再进一步验证这些交易的详细信息
以太坊 GHOST 协议
以太坊将出块时间设置为 10 秒左右,可能会导致大量分叉,按照最长链原则,较短的分叉链会被作废,从而打击矿工的积极性。同时出块时间减少,占据更多算力的大型矿池会更有优势,更早的占据最长合法链,对小矿工及系统的安全性不利
GHOST 协议的核心思想是:在选择主链(Longest Chain)的同时,需要考虑并行的分支链(Side Chain),从而提高了区块链的整体安全性和效率。在实现上,以太坊规定了“叔父区块”,所谓“叔父区块”就是指分支的区块。最长合法链的区块可以包含最多两个“叔父区块”,从而获得铸币所得的 1/32 作为奖励。同样的,“叔父区块”被包含也能获得铸币所得的 7/8 作为奖励。以太坊通过这种方式鼓励分支合并
叔父区块并不是无限的,以太坊规定当前区块的 7 代以内有共同祖先的才认为是“叔父区块”,且每远离自己一个区块的“叔父区块”得到的奖励就减少 1/8。同时,只有分支的第一个区块才认为是“叔父区块”并获得奖励,后面的区块无法获得奖励。这也是以太坊鼓励矿工们尽快合并,避免为了获得“叔父区块”奖励故意不合并以及防止分叉攻击的措施
以太坊挖矿算法
以太坊认为应该让所有人都能参与挖矿,而非使用专业的 ASIC 芯片的矿池占据主要算力。针对 ASIC 芯片用途单一的特点,以太坊的解决思路是:除了进行运算,还要增加对内存的访问,限制 ASIC 芯片
以太坊的思路是:提供一个很大的数组,矿工必须将该数组保存起来,并基于该数组挖矿。对于轻节点,由于它们只做验证,只需要保存一个较小的数组。轻节点保存的数组为 16MB 的 Cache,矿工保存的数组为 1G 的 DataSet(DAG)
Cache 为每一位填充伪随机数,填充过程是:首先设置 Seed 为种子,通过 Seed 进行一系列运算得到第一个数,之后每个数字都是通过前一个位置的值取哈希得到,这样的数组中取值存在前后依赖关系,只要知道前一个数和算法就可以推倒出来,所以叫伪随机数。每隔 30000 个区块会重新生成 Seed,并重新运计算得到新的 Cache,同时 Cache 容量增加初始大小的 1/128 即 128K
伪代码如下:
def mkcache(cache_size, seed):o = [hash(seed)]for i in range(1, cache_size):o.append(hash(o[-1]))return o
DAG 每个元素都是根据 Cache 经过一系列运算得来的,比如要填充 DAG 的第 i 位,分为以下步骤:
- 根据 i 算出对应 Cache 的下标,根据该下标对应的值与 i 算出一个 Mix
- 根据 Mix 算出对应 Cache 的下标,根据该下标对应的值与 Mix 算出一个新的 Mix
- 重复执行第 2 步,经过 256 次循环后,返回最终的 Mix,将该 Mix 填充到 DAG 的第 i 位
def calc_dataset_item(cache, i):cache_size = cache.sizemix= hash(cache[i % cache_size] ^ i)for j in range(256):cache_index = get_int_from_item(mix)mix= make_item(mix, cache[cache_index % cache_size])return hash(mix)
矿工根据区块 block header 和其中的 Nonce 值计算一个初始值 Mix,根据 Mix 求出对应 DAG 的下标,读取该下标的值以及其后一位的值,根据这两个值与 Mix 算出新的 Mix。重复上述步骤,对最终 Mix 计算出一个哈希值与挖矿难度目标阈值比较,若不符合就更换 Nonce。重复以上操作,直到最终哈希值符合难度要求
def hashimoto_full(header, nonce, full_size, dataset):mix = hash(header, nonce)for i in range(64):dataset_index = get_int_from_item(mix) % full_sizemix = make_item(mix, dataset[dataset_index])mix = make_item(mix, dataset[dataset_index +1])return hash(mix)
轻节点负责验证 Nonce 是否合法,同样是算出最终哈希值,但不需要保存 DAG,只需要根据 Cache 推倒对应位数的值即可
def hashimoto_light(header, nonce, full_size,cache)mix = hash(header, nonce)for i in range(64):dataset_index = get_int_from_ item(mix) % full_sizemix = make_item(mix,calc_dataset_item(cache, dataset_index))mix = make_item(mix,calc_dataset_item(cache, dataset_index + 1))return hash(mix)
以太坊挖矿难度调节
以太坊通过一个称为“挖矿难度调整算法”的机制来动态调节挖矿难度,每产生一个区块都会根据算法动态调节,旨在确保每个区块产生的平均时间大约为 15 秒,维持网络的稳定性和可靠性
算法的关键因素有如下:
- 目标时间:以太坊的目标是 15 秒产生一个新的区块,这个目标是由设计者决定的
- 实际产生时间:每个区块的时间戳记录了自身被挖挖出的实际时间,因此实际产生时间就是和上一次区块的时间戳的差值
- 难度因子:以太坊会比较实际产生时间和目标时间,自行计算并调整难度因子的值,实现动态调整挖矿难度
以太坊权益证明
Proof of Stake(PoS)是一种在区块链网络中选择验证者的方法,与 Proof of Work(PoW)不同,PoS不依赖于计算能力,而是依赖于验证者拥有的加密货币的数量,或称为质押(ETH)
想要成为验证者,需要质押一定数量的 ETH 到 Ethereum 2.0 网络中的智能合约。这些质押的 ETH 将会被锁定在合约中,并用作验证者的担保。质押的 ETH 数量越多,被选中的概率就越高。质押的 ETH 会随着时间推移而积累币龄,币龄可以理解为质押的 ETH 的持有时间,通常以时间为单位(比如天、周等)。持有 ETH 的时间越长,币龄越高
以太坊会定期进行随机抽签,以选择哪些验证者有资格创建新的区块。在这个过程中,每个验证者的被选中概率与其质押的 ETH 数量和币龄成正比。换句话说,质押的 ETH 越多、持有时间越长的验证者被选中的可能性就越大。一旦验证者被选中,他们将负责创建新的区块并将其添加到区块链,这个过程也包括验证交易等任务
验证者通过验证区块和交易获得网络费用作为奖励,如果验证者被发现进行不当行为,他们的质押资金可能会被没收或部分扣除,这是对不诚实或违规行为的严厉惩罚,严重违规的验证者可能会被网络排除,无法继续参与验证
以太坊智能合约
智能合约是一种基于区块链技术的自动化合约,它能够在没有第三方介入的情况下执行、管理和执行合约条款
所谓智能合约,就是一种运行在区块链上的程序,程序运行每次发生交易,就会产生一个交易区块。当区块被写入区块链时,其他节点也要执行区块中记录的代码逻辑,保证智能合约执行状态的一致性
以太坊提供了 EVM(Ethereum Virtual Machine)虚拟机来执行智能合约的字节码,并有很多限制,例如,不支持浮点运算(因为浮点数有不同的表示方法,不同架构的 CPU 运行的浮点计算精度都不同),不支持随机数,不支持从外部读取输入等等,这都是为了保证各节点执行的一致性
类似于 Java 源码被编译为 JVM 可执行的字节码,我们也需要一种高级语言来编写智能合约,然后编译成 EVM 的字节码。最常用的开发智能合约的语言是以太坊专门为其定制的 Solidity 语言
一个智能合约被编译后就是一段 EVM 字节码,将它部署在以太坊的区块链时,会根据部署者的地址和该地址的 nonce 分配一个合约地址,合约地址和账户地址的格式是没有区别的,但合约地址没有私钥,也就没有人能直接操作该地址的合约数据。要调用合约,唯一的方法是调用合约的公共函数。因此,合约不能主动执行,它只能被外部账户发起调用。如果一个合约要定期执行,那只能由线下服务器定期发起合约调用
此外,合约作为地址,可以接收 Ether,也可以发送 Ether。合约内部也可以存储数据,合约的数据存储在合约地址关联的存储上,这就使得合约具有了状态,可以实现比较复杂的逻辑,包括存款、取款等
合约在执行的过程中,可以调用其他已部署的合约,前提是知道其他合约的地址和函数签名。例如,一个合约可以调用另一个借贷合约的借款方法,再调用交易合约,最后再调用还款方法,实现所谓的“闪电贷”(即在一个合约调用中实现借款-交易-还款)功能
当一个合约编写完成并成功编译后,就可以把它部署到以太坊上。合约部署后将自动获得一个地址,通过该地址即可访问合约。如果多次部署同一个合约,那么它们的地址是不一致的,也就是分别独立的合约
任何外部账户都可以发起对合约的函数调用。如果调用只读方法,因为不改变合约状态,所以任何时刻都可以调用,且不需要签名,也不需要消耗 Gas。但如果调用写入方法,就需要签名提交一个交易,并消耗一定的 Gas。在一个交易中,只能调用一个合约的一个写入方法。无需考虑并发和同步的问题,因为以太坊交易的写入是严格串行的