ABC232G

大致题意

你有一个 \(n\) 个点的有向完全图。

每个点有两个属性 \(a_i\) 和 \(b_i\)。\(u \to v\) 的边的权值是 \((a_u+b_v) \bmod m\)。

给你 \(n\) , \(m\) 和 \(\{a_i\}\) 以及 \(\{b_i\}\) , 求 \(1\) 到 \(n\) 的最短路。

• $ 2\ \leq\ N\ \leq\ 2\ \times\ 10^5 $
• $ 2\ \leq\ M\ \leq\ 10^9 $

Solution

观察题面，发现如果没有 \(\bmod m\) 是容易的，所以先考虑怎么处理 \(\bmod m\)

容易想到 \(a_u+b_v \leq 2m-2\)，可以变为：

• 当 \(a_u+b_v \leq m-1\) 时，边权为 \(a_u+b_v\)
• 当 \(m \leq a_u+b_v \leq 2m-2\) 时，边权为 \(a_u+b_v-m\)

接下来我们可以想到，将有 \(-m\) 和没有的分开来。

所以考虑将 \(b\) 数组排序，这样对于一个确定的 \(u\) 一段前缀的边权是 \(a_u+b_v\) ，一段后缀的边权是 \(a_u+b_v-m\)

于是对于每个点 \(u\) 可以建出类似下图的东西

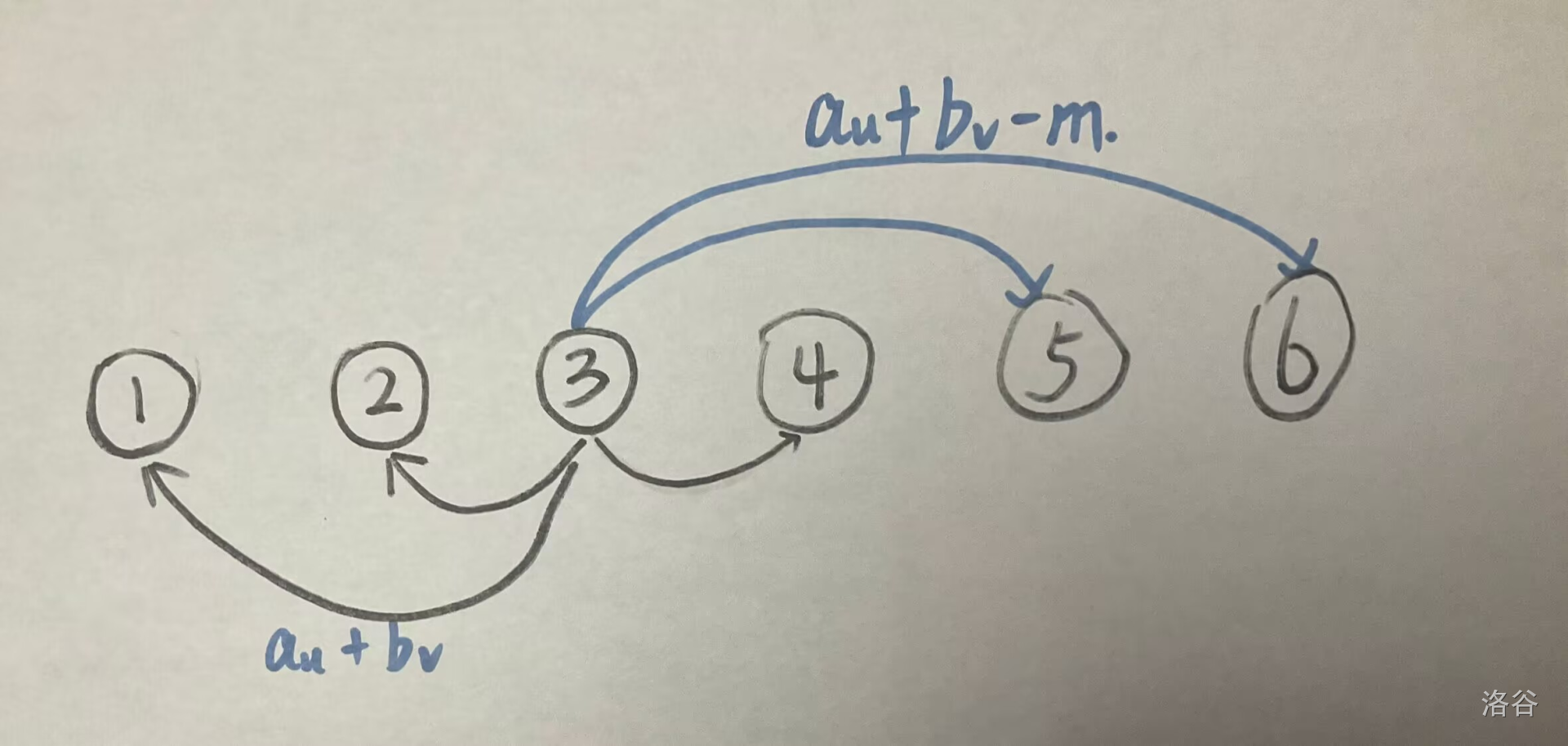
然而发现边数是 \(O(n^2)\)，考虑到一个点总是对一段连续的后缀连边时边权有 \(-m\)

于是想到可以用前缀和优化建图

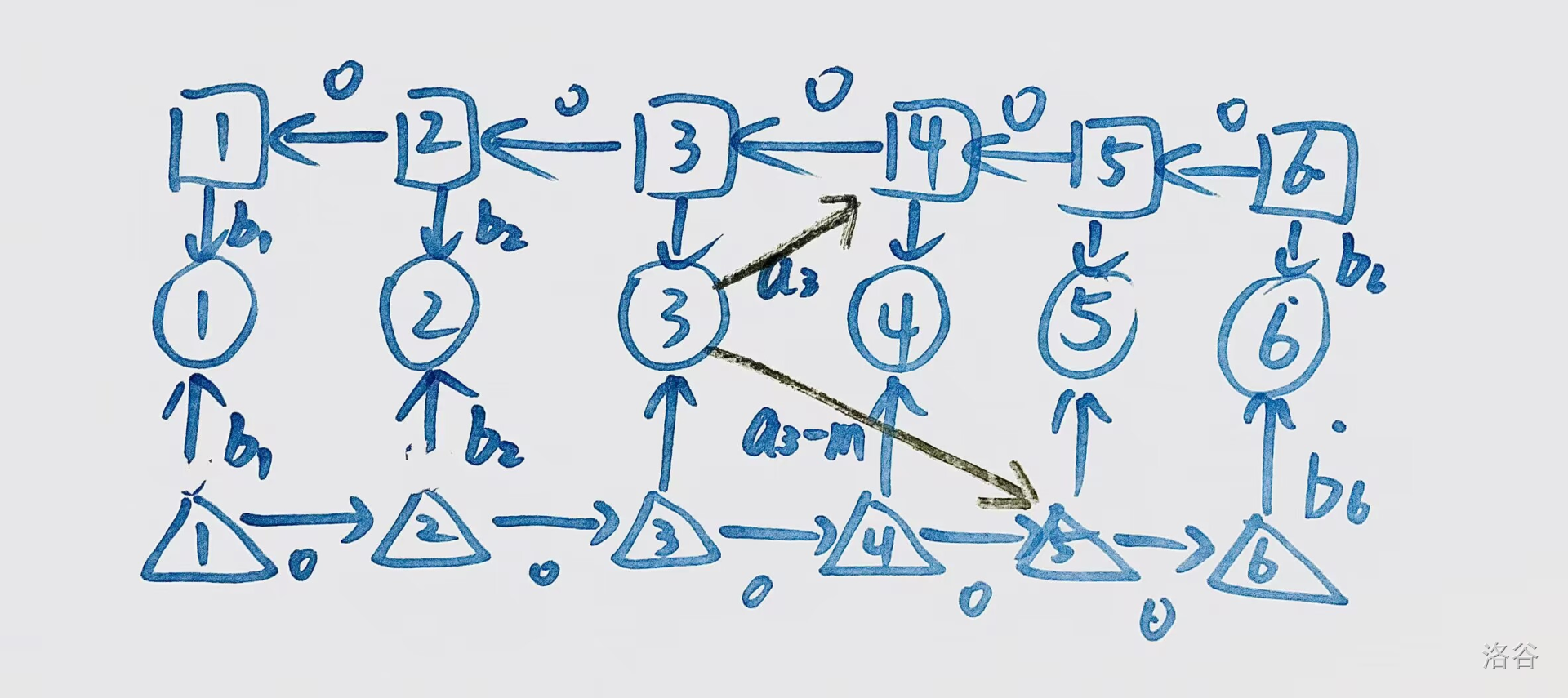
于是得到了一个边数 \(O(6n)\) 的图，有负权边

所以只能使用SPFA

容易发现，它真的已经死了

喜提TLE

边数已经足够优，考虑如何消除负权边，这样就可以跑dij

原本建图中的负权边只在圈圈连到三角包的时候有

\(-m\) 是必须存在的，而原题中只有 \(a_u+b_v \leq m\)，所以只能将负权边该为 \(a_u+b_v-m\)

（比如图中圆圈3连到三角包5的边权值该为 \(a_3+b_5-m\)）

考虑如何弥补正确性问题

既然都有前缀和优化建图了，那自然可以使用差分

可以得到如下的一个建图

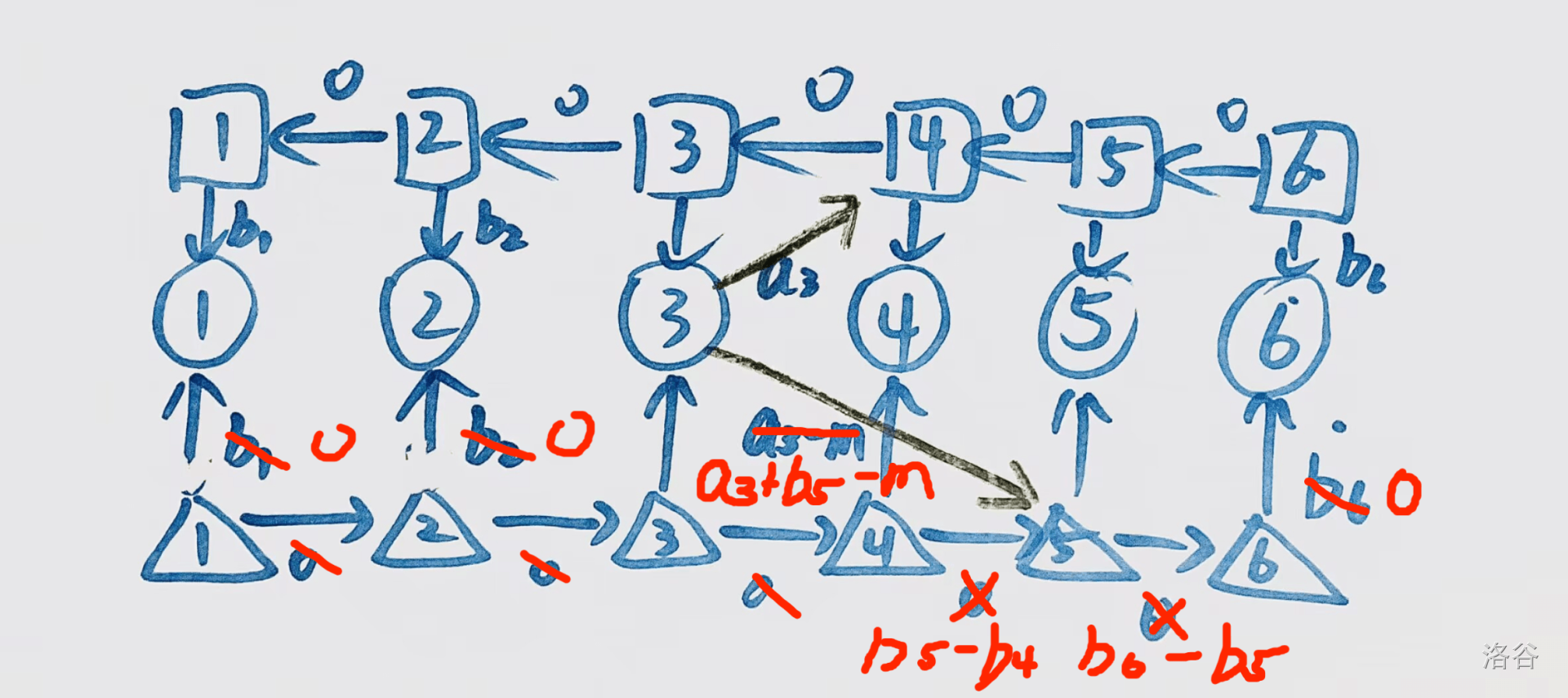
于是跑一个dij即可通过，复杂度为 \(O(n\log n+m\log n)\)