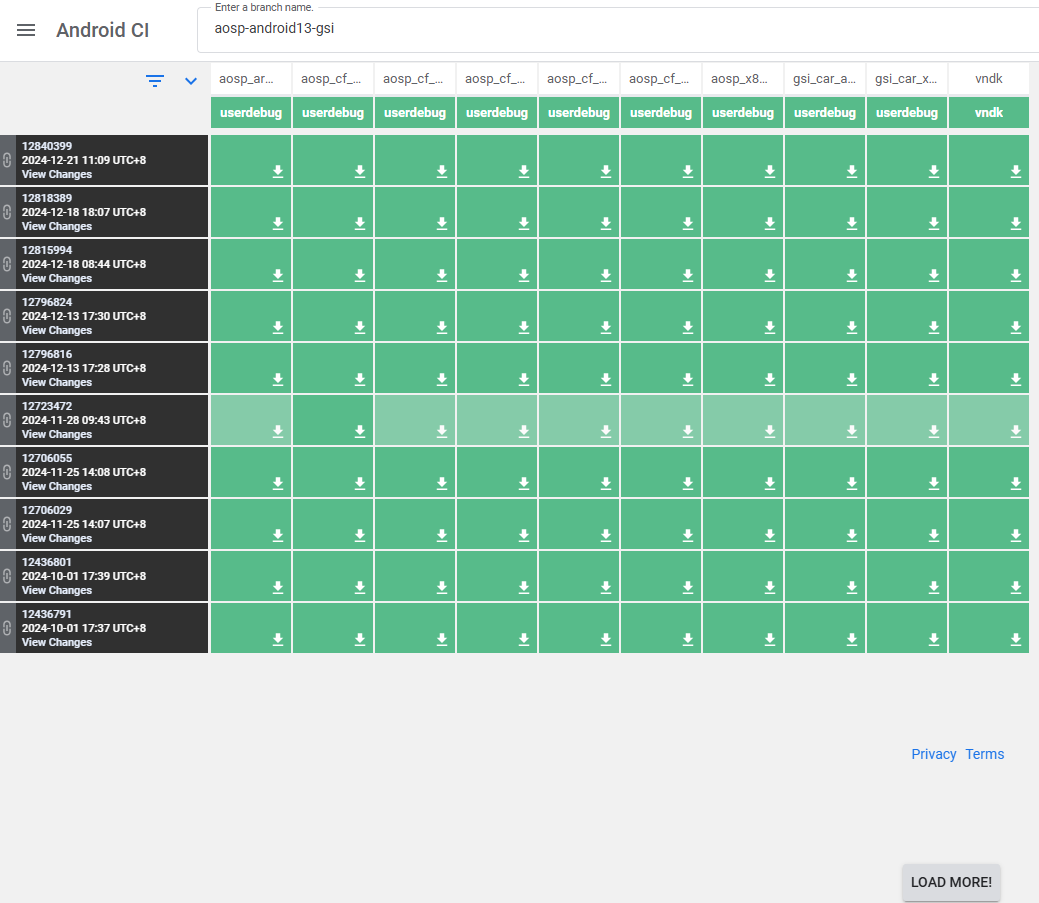
好东西,因为曾经在一次模拟赛的20分暴力中用到了,而我因为不会痛失20暴力分
树形DP
树形DP一般在一棵有根树上递归操作
嗯还是啥都不知道,上例题
【YbtOj】例题
A.树上求和
小小求和,拿捏
在从子节点转到父节点时,有着“二选一”的限制,所以设置状态时需要表示当前节点是否被选
于是乎,设状态 \(f_{x,opt}\) ,当 \(opt=0\) 时表示不选当前节点的最大和,反之则是选当前节点的最大和。于是乎就有转移方程
\[f_{x,0}=\Sigma\ max(f_{v,0},f_{v,1})\ ,f_{x,1}=\Sigma{f_{v,0}}+r_{x}
\]
然后就做完了
贴
#incIude <bits/stdc++.h>
#define int long long
using namespace std;
const int N=6e3+5;
int n,r[N];
vector <int> tr[N];
int d[N],root,f[N][2];void dfs(int x)
{int res1=0,res2=0;int _size=tr[x].size();for (int i=0;i<_size;i++){int v=tr[x][i];dfs(v);res1+=max(f[v][0],f[v][1]);res2+=f[v][0];}f[x][0]=res1,f[x][1]=r[x]+res2;
}
signed main()
{scanf("%lld",&n);for (int i=1;i<=n;i++) scanf("%lld",&r[i]);for (int i=1,u,v;i<n;i++){scanf("%lld%lld",&u,&v);tr[v].push_back(u);d[u]++;}for (int i=1;i<=n;i++) if (!d[i]) { root=i; break; }dfs(root);printf("%lld",max(f[root][0],f[root][1]));return 0;
}
B.结点覆盖
小小覆盖,拿捏
一个点被覆盖到只有三种情况:选它的子节点,选自己,选它的父节点。于是乎,状态 \(f_{x,pot}\) 的 \(opt\) 分别代表上三种情况,然后对应的转移就行了
贴
#incIude <bits/stdc++.h>
#define int long long
using namespace std;
const int N=1505;
int n,k[N];
int d[N],root;
vector <int> tr[N];
int f[N][3];void dfs(int x)
{int res0=0,res1=0,res2=0;int _size=tr[x].size();for (int i=0;i<_size;i++){int v=tr[x][i];dfs(v);res0+=min(f[v][1],f[v][0]);res1+=min(f[v][0],min(f[v][1],f[v][2]));res2+=min(f[v][0],f[v][1]);}f[x][1]=res1+k[x],f[x][2]=res2;if (_size==0) return ;for (int i=0;i<_size;i++){int v=tr[x][i];f[x][0]=min(f[x][0],res0-min(f[v][0],f[v][1])+f[v][1]);}
}
signed main()
{memset(f,0x3f,sizeof f);scanf("%lld",&n);for (int i=1,x,m;i<=n;i++){scanf("%lld",&x);scanf("%lld%lld",&k[x],&m);for (int j=1,v;j<=m;j++){scanf("%lld",&v);tr[x].push_back(v);d[v]++;}}for (int i=1;i<=n;i++) if (!d[i]) { root=i; break; }dfs(root);printf("%lld",min(f[root][0],f[root][1]));return 0;
}