人工智能基础导论
绪论
人工智能的主要流派
- 符号主义(逻辑主义)
- 连接主义(仿生学派)
- 行为主义(控制论)
符号主义:数理逻辑→逻辑演绎系统→启发式算法→专家系统→知识工程理论与技术(主流)
- 缺点:符号主义的核心是知识表示,那么对于像感知、形象思维、模式识别等问题,又该如何“表示”呢?
连接主义原理:神经网络及神经网络间的连接机制与学习算法
- 缺点:难以建立起神经网络中间语言与外部环境语言之间沟通渠道,且缺乏通用性,一般一个网络只能解决一个问题
行为主义原理:控制论及感知-动作型控制系统。
研究方法
遗传演化主义:模拟生物在自然环境中的遗传进化选择假设过程而形成的一种自适应全局优化概率搜索方法。其模仿的主要生物机制包括:
- 遗传与变异:DNA及其遗传机制、概率性变异和出错性
- 选择与进化:环境选择压、优胜劣汰的演化机制。
群体计算主义:由智能主体构成的集群系统,称为智能主体集群系统。在这种系统中,每个智能主体都是相互平等和相对独立的,它们通过知识信息的相互交流来完成任何单独智能主体均无法完成的复杂智能任务、涌现出更高级的智能行为来。也就是整体大于部分之和假设。
知识表示方法
状态空间法


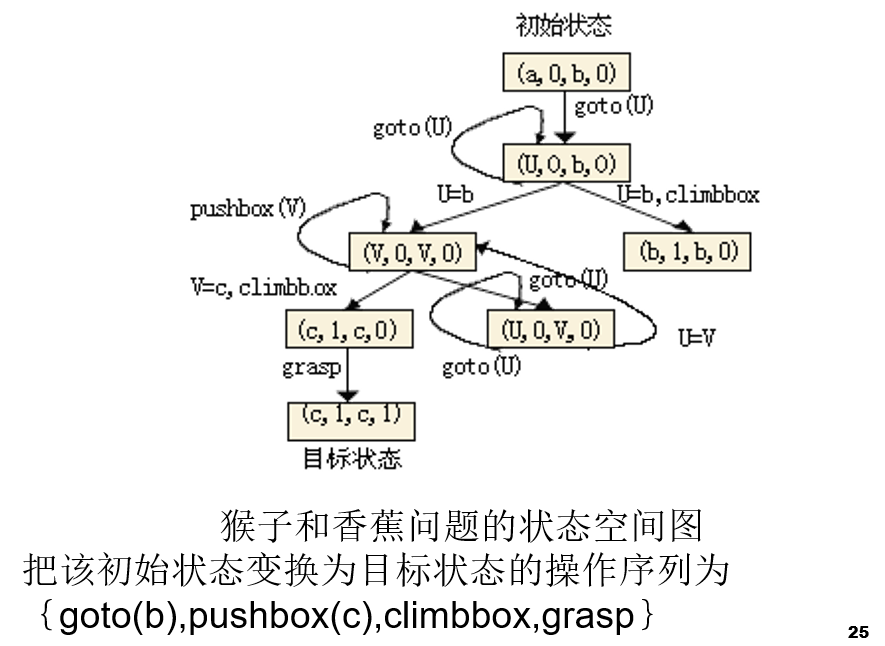
问题规约法
先把问题分解为子问题和子-子问题,然后解决较小的问题。(分治与递归)


谓词演算法
能够判断真假(具有真假意义的)的陈述句。命题的判断结果只取两个值:真、假。
谓词比命题更加细致地刻画了知识。 可以代表变化的情况, 建立起不同知识之间的联系。
合取式:p与q,记做p ∧ q 。
析取式:p或q,记做p ∨ q 。
否定式:p的否定式记做~p 。
蕴含式:如果p则q,记做p → q 。
等价式:p当且仅当q,记做p <=> q
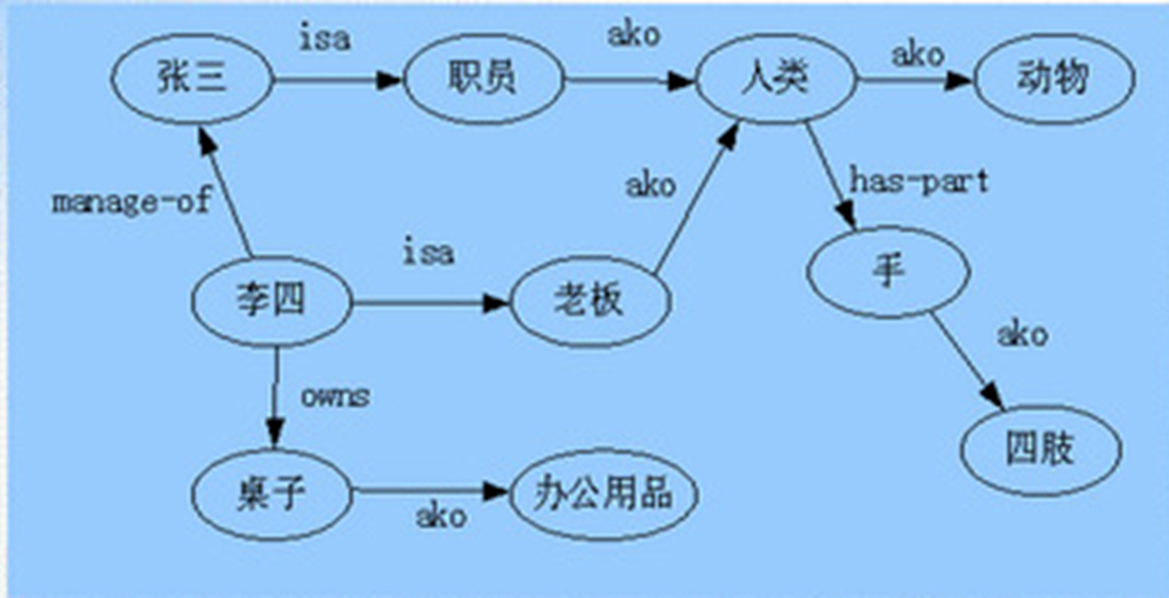
语义网络法
框架表示
心理学的研究结果表明,在人类日常的思维和理解活动中,当分析和解释遇到的新情况时,要使用到过去经验中积累的知识。当然,我们无法把过去的经验一一都存在脑子里,而只能以一个通用的数据结构的形式存储以往的经验。这样的数据结构称为框架。
框架包含物体必须具有的属性。
选择和当前情况相对应的当前框架片断,把这个框架片断和候补框架相匹配。选择最佳匹配。如果当前的框架,总的来说差不多是可以接受的,则许多已经做的,有关建立子结构以填入这个框架的工作将可保留。
面向对象表示
面向对象表示法中的对象指物体,消息指物体间的联系,通过发送消息使对象间相互作用来求得所需的结果。
剧本表示
剧本是框架的一种特殊形式,它用一组槽来描述某些事件的发生序列。(有时间序列)
过程表示
过程式表示就是将有关某一问题领域的知识,连同如何使用这些知识的方法,均隐式地表达为一个求解问题的过程。(而语义网络、框架、剧本等是知识的一种显示表达形式)
搜索推理技术
从问题表示到问题的解决,有一个求解的过程。搜索推理研究的是实现求解的过程,采用的基本方法包括搜索和推理。
搜索:从大量事物构成的状态空间中寻找某一特定对象的过程。
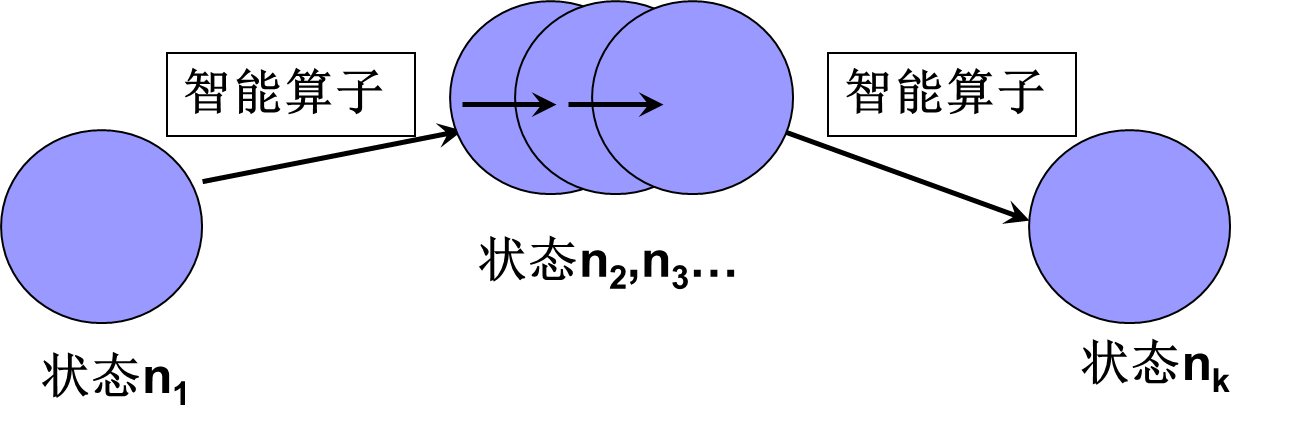
一般搜索系统
人工智能解题程序的三个基本要素:
-
一个综合数据库: 描述问题所需的基本数据,随解题过程的推进而变化。
-
一组智能算子:给出作用于综合数据库的某种变化规则。
-
一个解释程序:包含了智能算子的选用与解释,在解题中起控制作用。
盲目搜索系统
-
盲目搜索又叫做无信息搜索,一般只适用于求解比较简单的问题。
-
盲目搜索方法包括宽度优先搜索、深度优先搜索、等代价搜索等。
-
没有使用知识作为指导的搜索。
-
对搜索空间中的状态进行穷举,容易导致组合爆炸。
启发式搜索
利用相关知识或信息可以大大降低搜索的代价,并找到较满意的解。
- A 算法:是一种启发式搜索算法。它通过评估函数\(f(n) = g(n) + h(n)\)来对节点进行评估,其中\(g(n)\)表示从初始节点到节点的实际代价,\(h(n)\)是从节点到目标节点的启发式估计代价。
- A * 算法:实际上是 A 算法的一种特殊情况。A * 算法要求启发式函数\(h(n)\)满足一定的条件,即它是可采纳的。可采纳性意味着永远不会高估从节点到目标节点的实际代价。
博弈搜索(敌对搜索)
特性:博弈双方的对抗性;博弈各方都努力寻找各自获胜状态格局,同时也努力阻止对方出现获胜状态局。
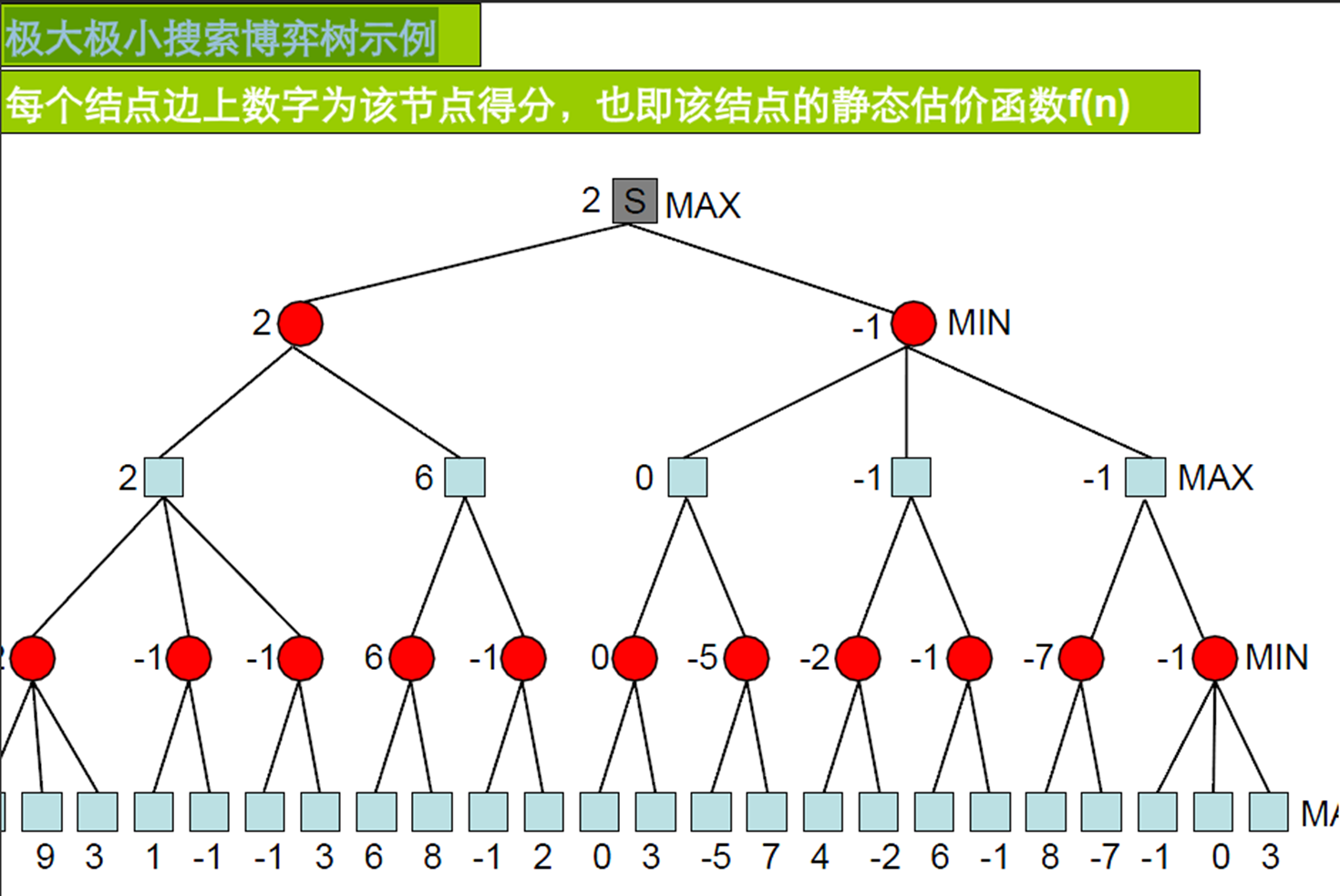
¨e****(P) = MAX的赢线数 – MIN的赢线数

问题:
启发式博弈搜索策略 - 将扩展生成博弈树的过程与计算、评价及确定最优走步的过程完全分开进行,导致了搜索效率的低下。
对策:
α - β剪枝技术 - 在生成博弈树同时计算和评价棋局节点,对不必要展开的节点进行剪枝,可减少许多不必要节点的生成和计算工作量,提高搜索效率。
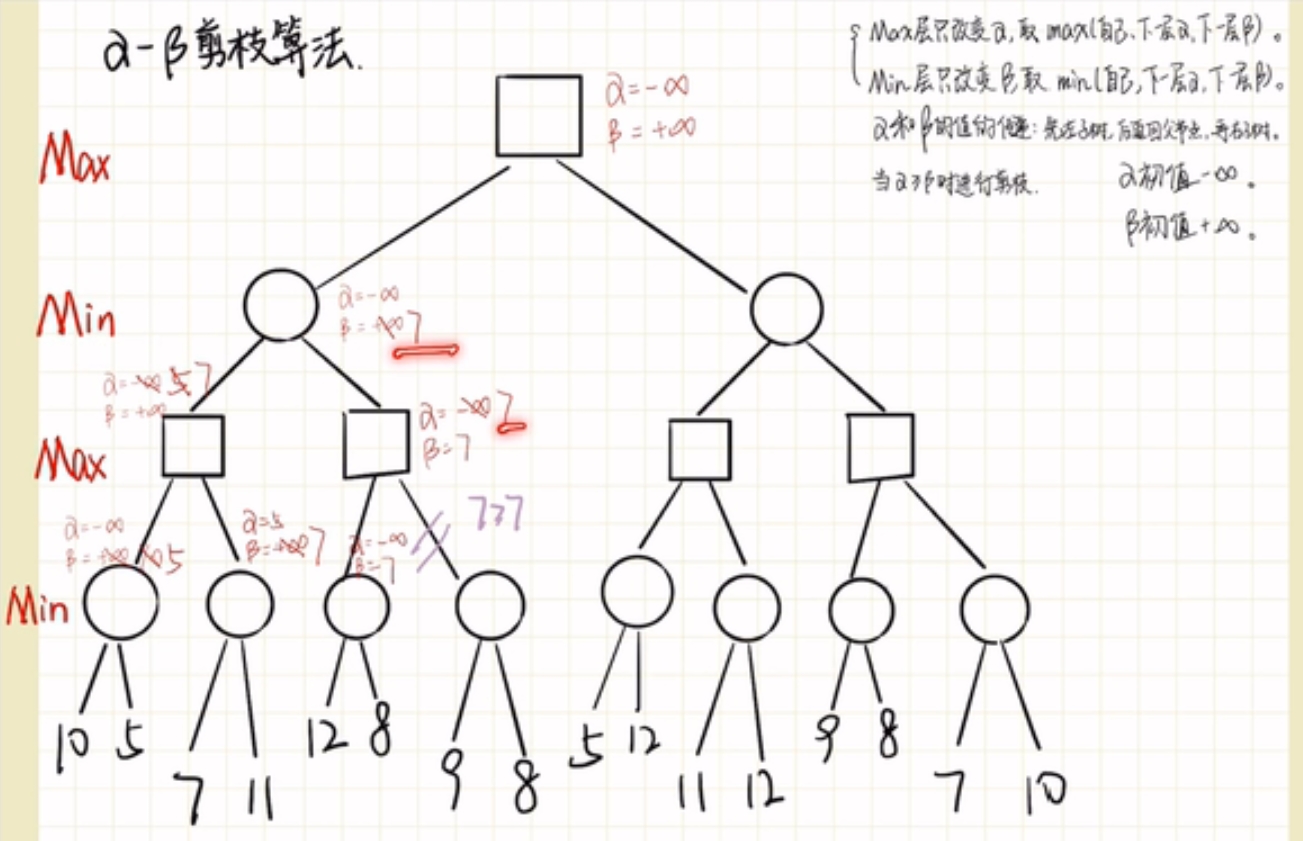
-
当任何MIN节点的值小于等于它的MAX的祖先节点的值,则可中止该MIN节点以下的搜索。
-
当任何MAX节点的值大于等于它的MIN的祖先节点的值,则可中止该MAX节点以下的搜索。
谓词逻辑法
该方法是一种比较常见的知识表示方法。除了广泛应用于各类专家系统之中外,主要运用于机器推理和定理证明之中。
例子:
今天有雨雪,有些人会跌跤。
本语句可理解为“若今天下雨又下雪,则存在x,x是人且x会跌跤”。
-
令 R: 今天下雨,S: 今天下雪,
-
M(x): x是人,F(x): x会跌跤,
-
则本语句可表示为:\(R \land S \to (\exist x)(M(x) \land F(x))\)
常用的一些等价关系:
-
\(\neg(\neg p) = p\)
-
$P \to Q = \neg P \or Q $
-
\(P \to Q = \neg Q \to \neg P\)
置换:
设有表达式P[x,f(y),B] ,对于置换:s1={z/x,w/y},s2={A/y}
分别有:
-
P[x,f(y),B]s1= P[z,f(w),B]
-
P[x,f(y),B]s2= P[x,f(A),B]
变换谓词演算公式为一个子句集可由下列九个步骤:
(1)消去蕴涵符号
(2)减少否定符号的辖域
(3)对变量标准化
(4)消去存在量词
(5)化为前束形
(6)把母式化为合取
(7)消去全称量词
(8)消去连词符号
(9)更换变量名称
反演求解过程
把要解决的问题作为一个要证明的命题,其目标公式被否定并化成子句形,然后添加到命题公式集中去,把消解反演系统应用于联合集,并推导出一个空子句(NIL),产生矛盾,这说明目标公式的否定式不成立,即有目标公式成立,问题得到解决。
如果一个公式集不能被任一解释所满足,那么这个公式是不可满足的。因此,如果L在逻辑上遵循S,那么S∪{~L}是不可满足的。
例子:

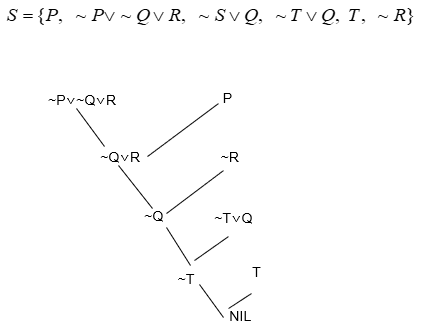
消解求解过程



规则演绎系统
反演消解(归结)方法虽然简单易行、自动化程度高,但也存在两点严重的不足:
-
子句形是一种低效率的表达式。高度统一的子句形式会丢失隐含的启发知 ,如条件式变成了析取式就会如此。
-
与人类自然思维脱节,不直观,不利于构建实用性专家系统。
对于一些复杂的系统和问题,简单使用以前所介绍的搜索方法和消解方法难以解决。规则演绎系统及其它一些方法(如产生式系统、系统组织技术、不确定性推理和非单调推理等)则更适合解决这些复杂的系统和问题。
规则演绎系统采用易于叙述的if-then规则来求解问题。


规则正向演绎系统
正向规则演绎系统是从事实到目标进行操作,即从状况条件到动作进行推理的,也就是从if到then的方向进行推理的。

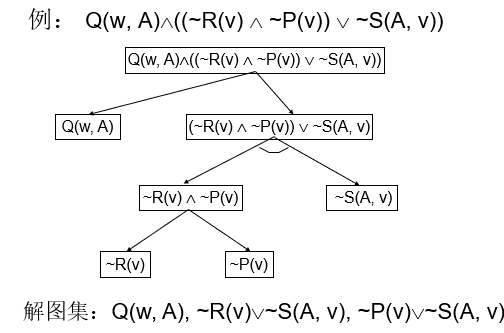
规则逆向演绎系统




双向控制策略
控制策略宜采用正逆向结合的演绎方法。
1混合采用正逆向推理方法,形成双向演绎推理方法
2)分割任务,不同的子任务采用不同控制策略的演绎推理
3)终止条件判断:涉及两个与或图结构之间的交接处