分段解密
加密脚本如下:
import sysdef abc(First): First = c_uint32(First)return Firstdef enflag(i, j):a = 32tt = 0x9e3779b9b = [0,0]First = abc(i[0])Second = abc(i[1])add = abc(0)add=add.valuewhile(a>0):add += ttFirst.value += ( Second.value << 4 ) + j[0] ^ Second.value + add ^ ( Second.value >> 5 ) + j[1]Second.value += ( First.value << 4 ) + j[2] ^ First.value + add ^ ( First.value >> 5 ) + j[3]a = a - 1b[0] = First.valueb[1] = Second.valuereturn bdef str_encoding(ecryptText, PK):List = []ecryptText += (8 - len(ecryptText) % 8) * chr(0)for m in range(len(ecryptText)/8):p = 0q = 0for n in range(4):p+= ord(ecryptText[m*8+n]) << (4-n-1)*8q+= ord(ecryptText[m*8+n+4]) << (4-n-1)*8List.append(enflag([p,q],PK))return Listif __name__ == "__main__":flag = xxxxPK = [141,262,339,425]crypto = str_encoding(flag,PK)print(crypto)
crypto文件内容如下:
[[3202805436L, 509716930L], [3140667873L, 1667141091L], [3173275598L, 2248305098L], [709283154L, 3416762332L]]
解题脚本如下:

组合得到{flag_s1_LINJI_WUSHU1}galf
逆序得到flag}1UHSUW_IJNIL_1s_galf{
把括号翻个位置即可得到flag
flag{1UHSUW_IJNIL_1s_galf}
BabyRSA
得到一个flag.txt和私钥文件

这就是密文c了
然后进行私钥解析
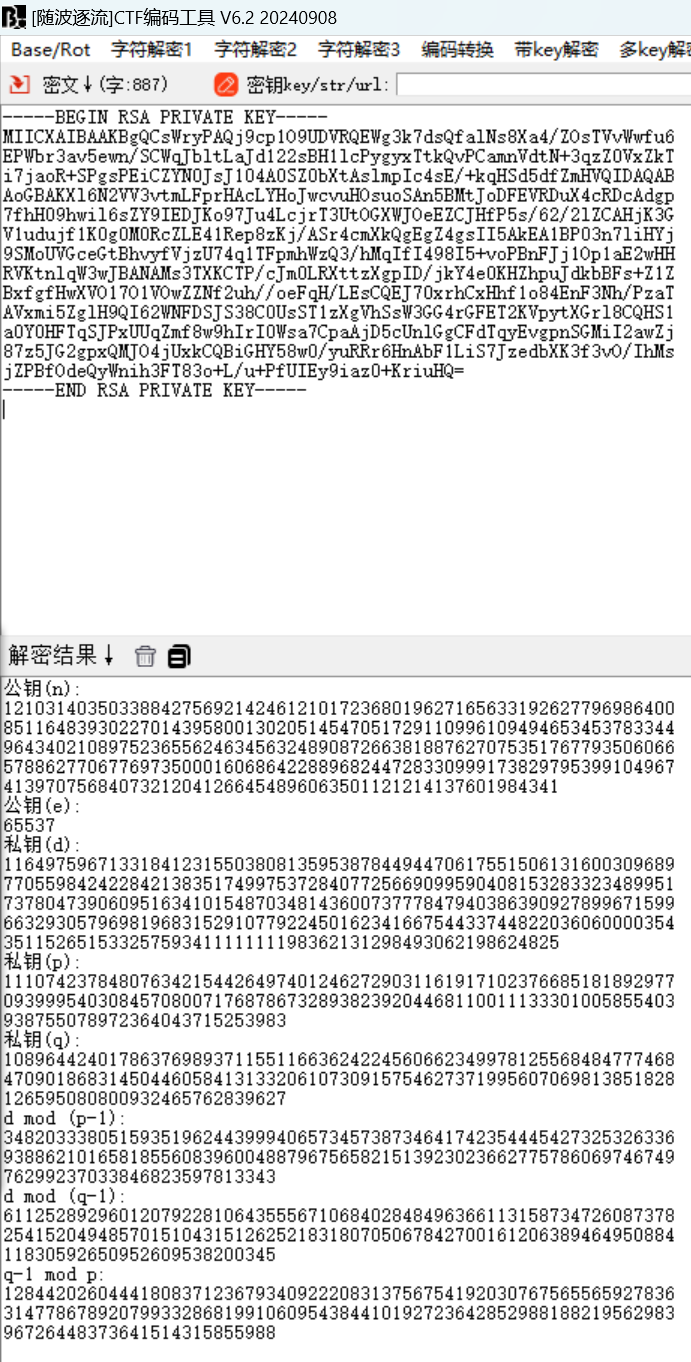
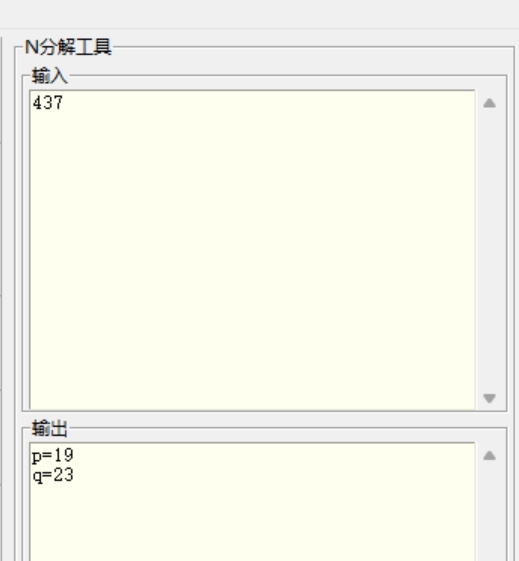
nedpq值全部已知了
扔到RSA工具里面
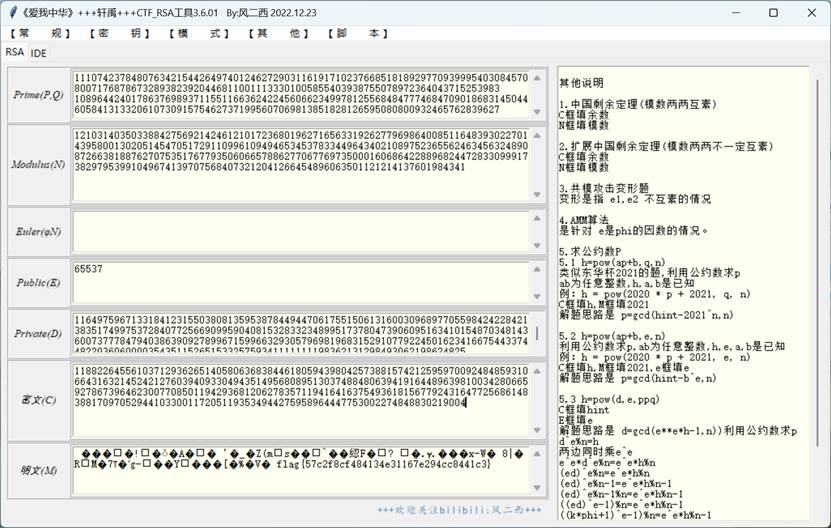
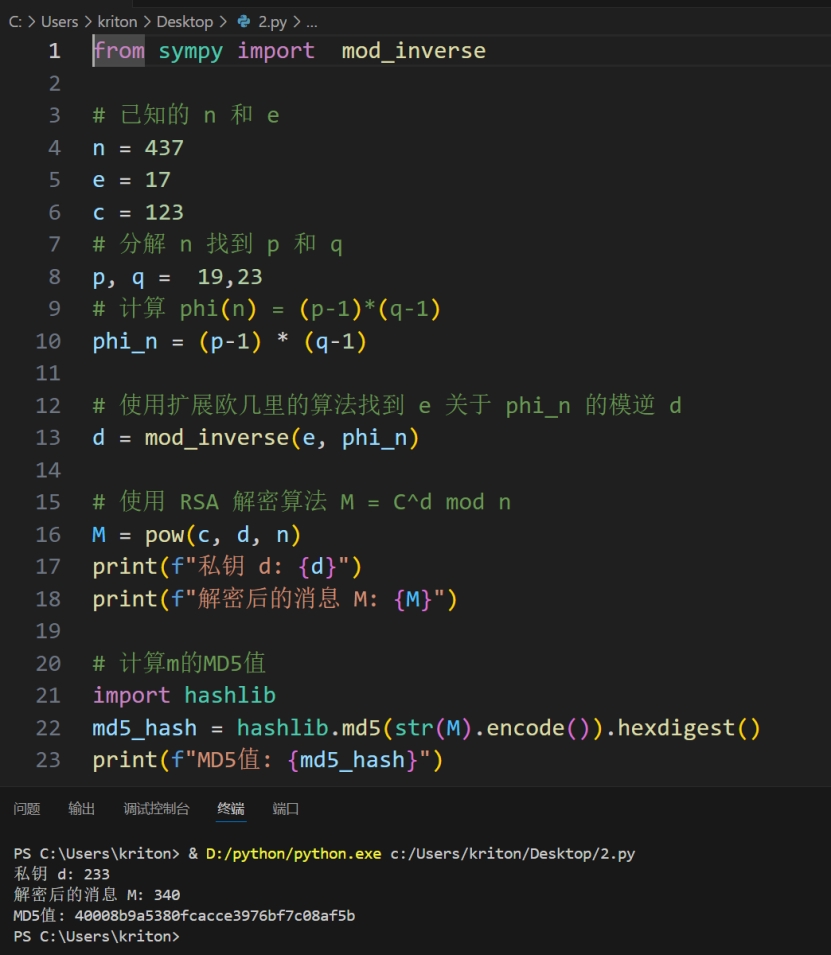
计算明文转字符即可获得flag
Wp是用脚本跑出来的,脚本如下
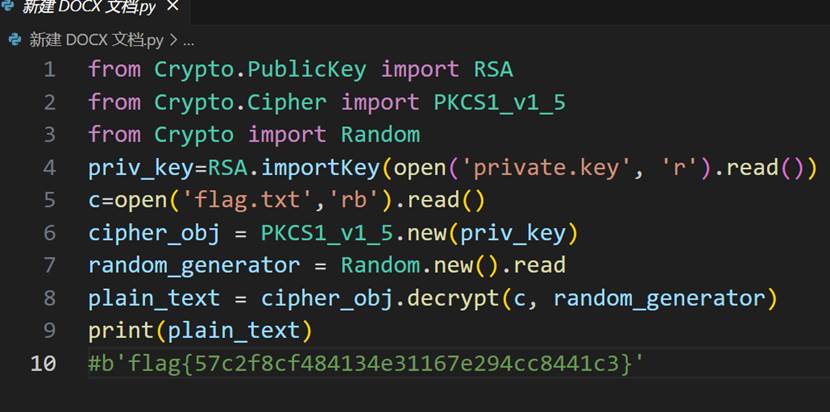
EasyRSA
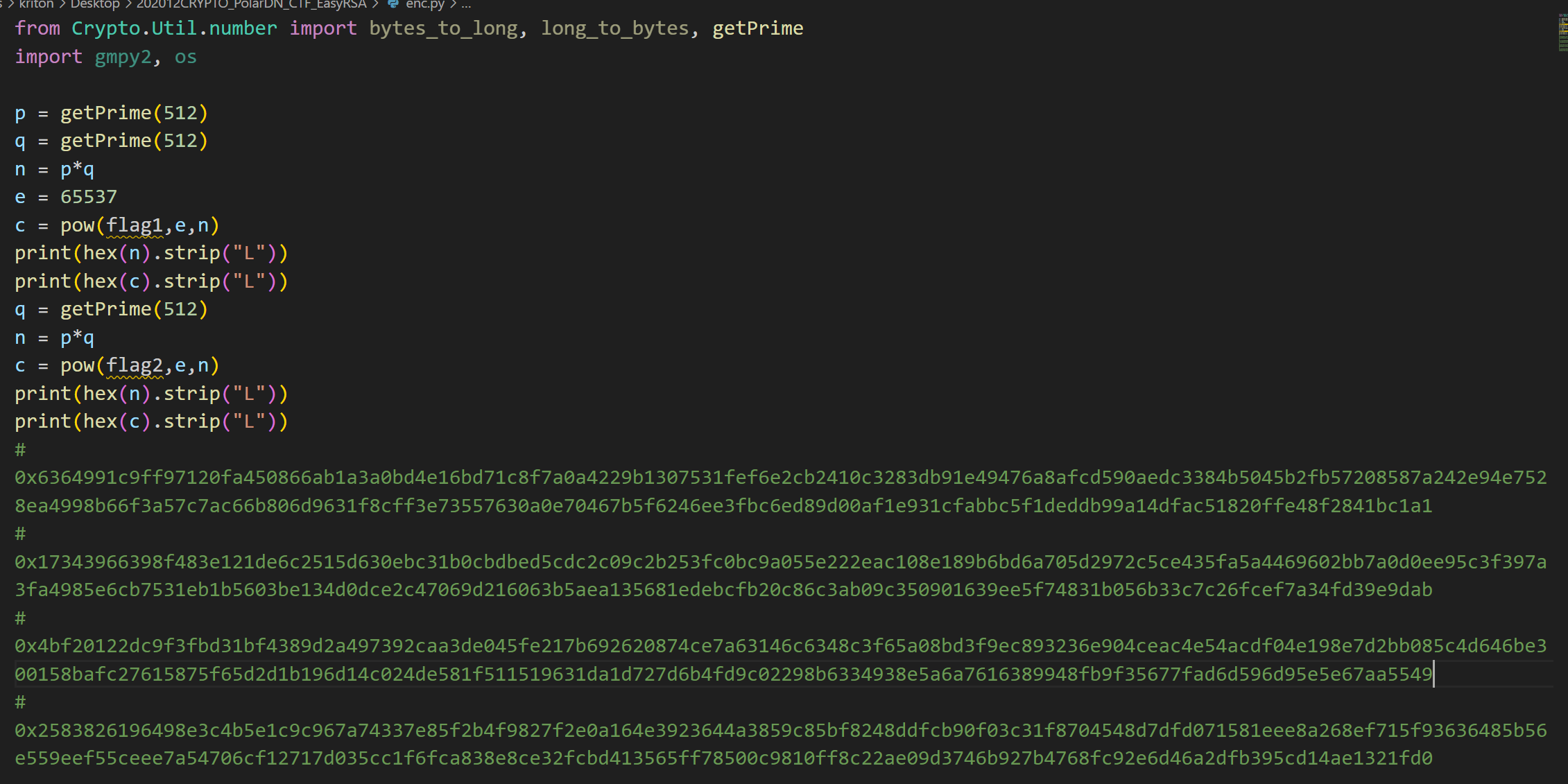
在加密脚本中将flag分为两部分,两组公钥具有同一个p又同时给出了n1、n2、c1、c2,其中n1和n2具有公因数p,所以应先求出p。
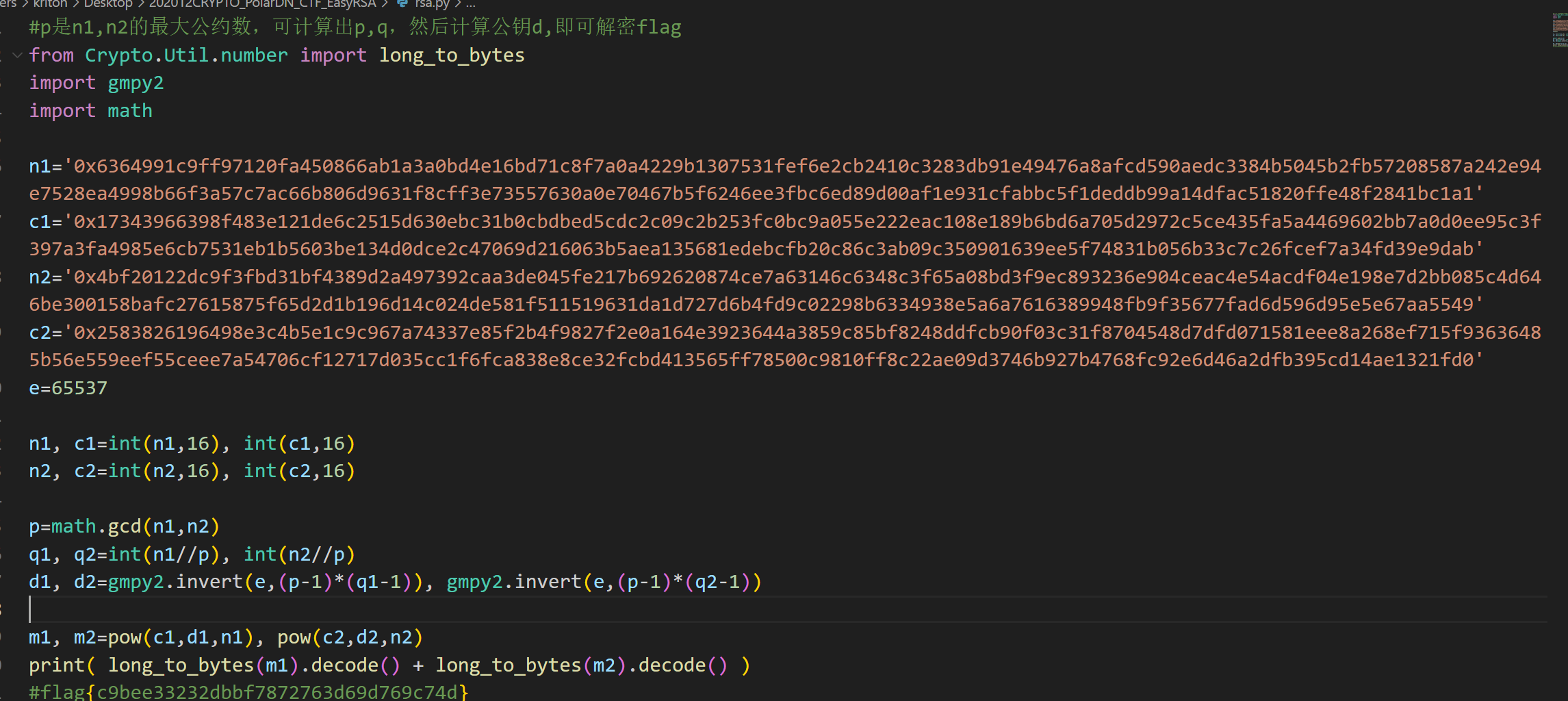
这里我们先将所有值转为十六进制,然后用gcd()计算最大公约数,求得p之后,利用n=p*q的关系求得两组q,进而计算各组的私钥值,最后利用pow函数计算明文
classic
txt内容如下:
FGAFDAXAGXDGDXAXAGDDAFDAAFFGFDAFGX
先对其进行倒序,得到真正的密文
s = 'FGAFDAXAGXDGDXAXAGDDAFDAAFFGFDAFGX'
print(s[::-1])
然后使用adfgx在线解密网站,秘钥方阵默认,key为题目classic
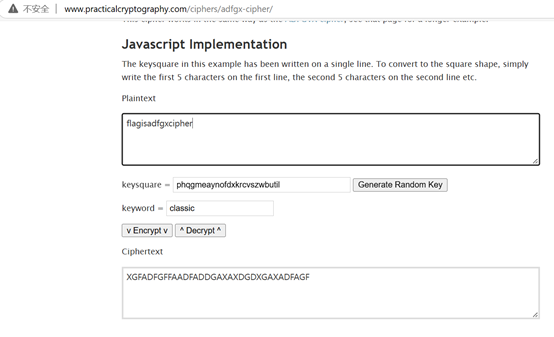
将adfgxcipher进行md5加密,提交flag
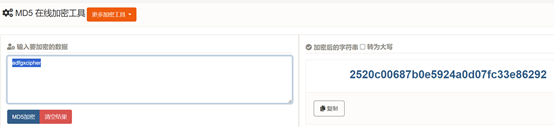
波奥比利斯
hint:74686973206973206D643520426F6F6D216cd29f23de85b1309128ff736c7efbf6
efa4e6f5c6359cc2eadc5d731716468e
408a9c4a79800232ac656249af3162eb
6adff50182df8ad3b836f7fb9dc5c4ab
6ae0af41daeb79509ab3b47b5ed8a687key:qwertyuiopasdfghjklzxcvbn
得到一个txt文件,文件名提示是波利比奥斯加密
Hint文本可用base16解码或者16进制转字符获得提示
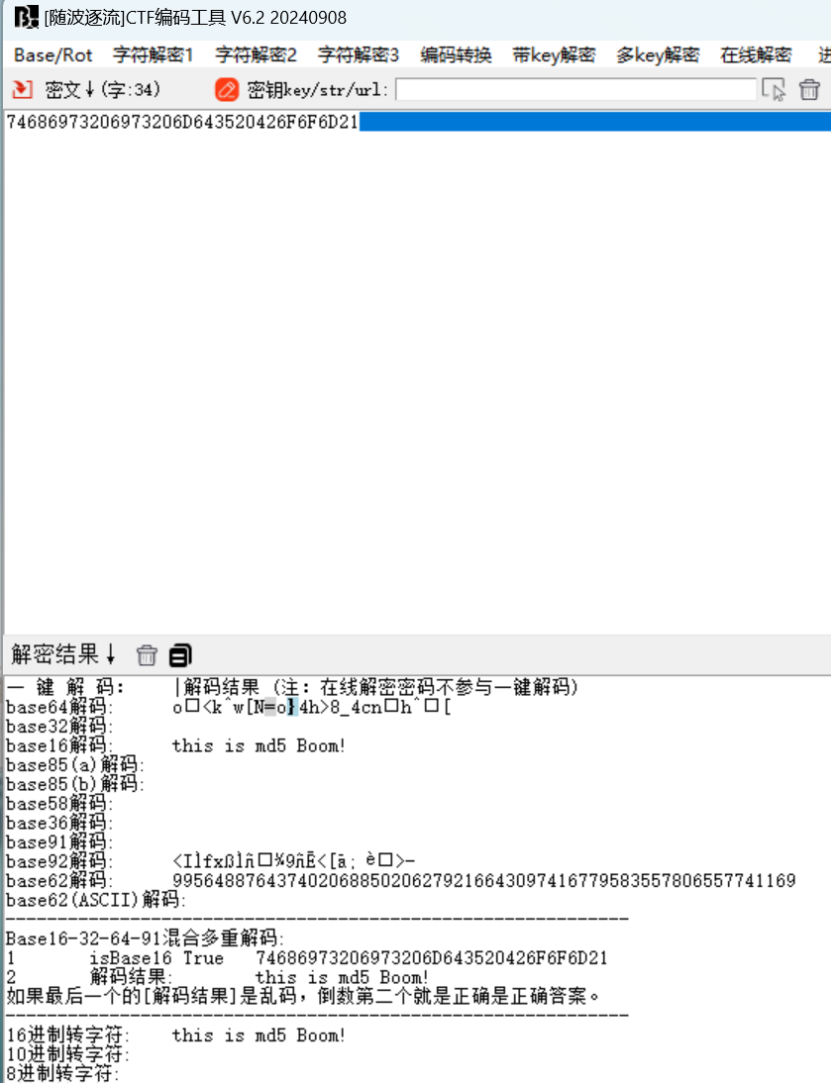
Md5爆破,利用MD5Crack3工具或者MD5在线解密网站
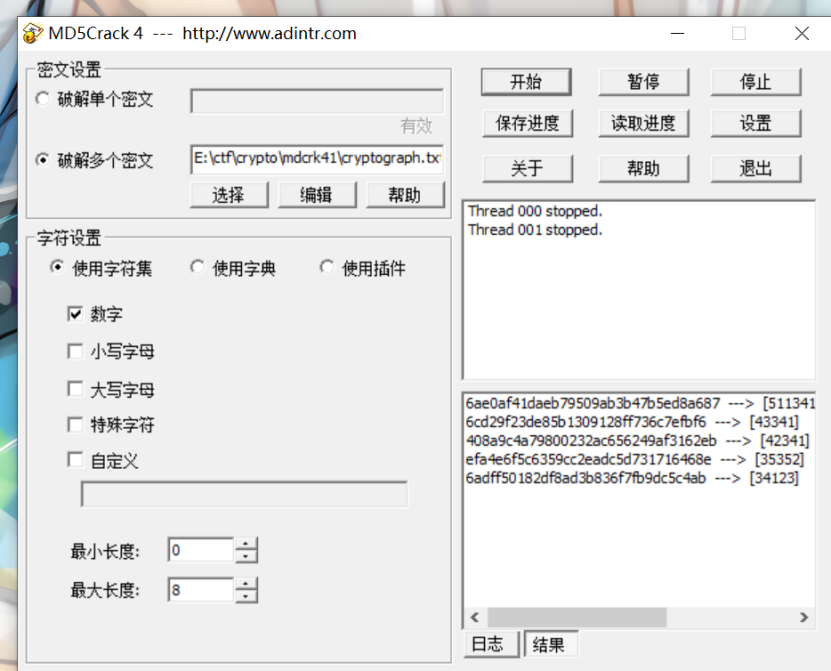
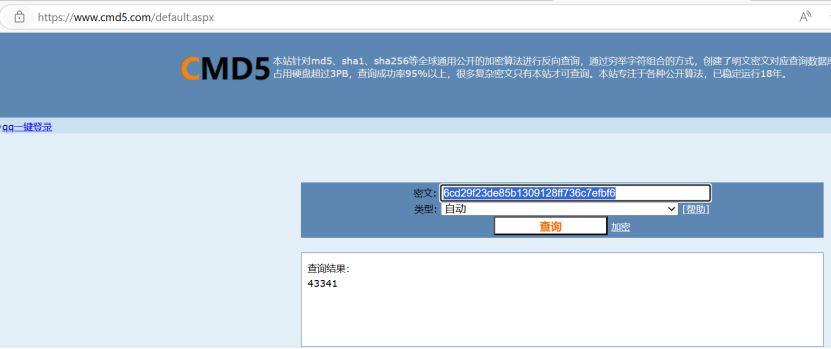
跟在线得到的结果一致,按照32位md5的顺序拼接排列爆破结果,得到
43341353524234134123511341
Key已给出,利用波利比奥斯在线网站解密
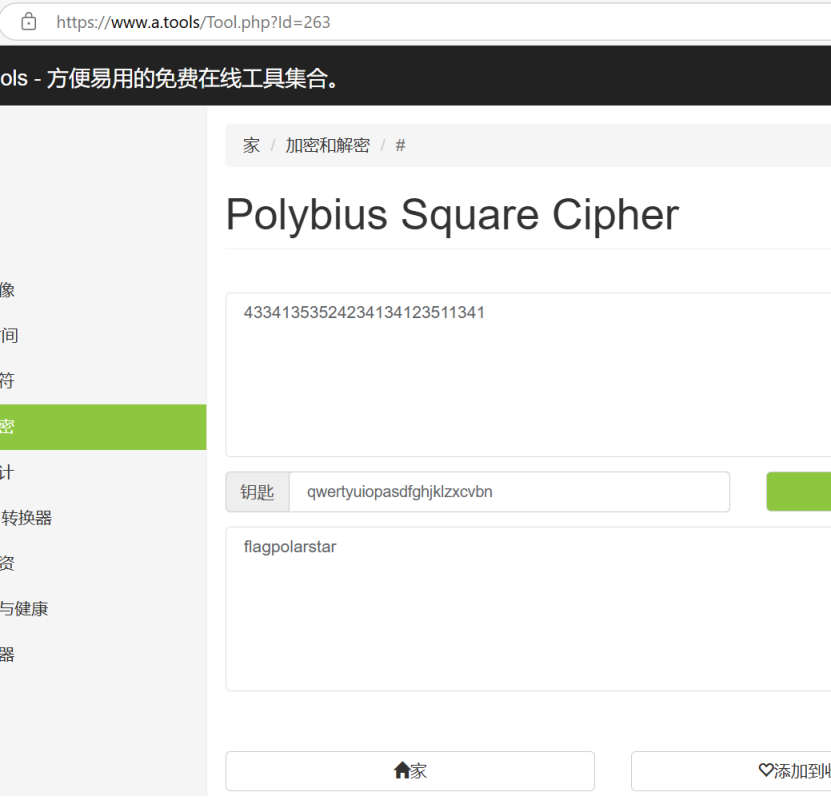
四个正方形
明文:cajfedlarc
hint:两个key是该密码创始人的姓名
题目提示是四方密码
百度一下知道key1=felix,key2=delastelle,去掉重复字母,key1=felix,key2=delast,进行构建矩阵。
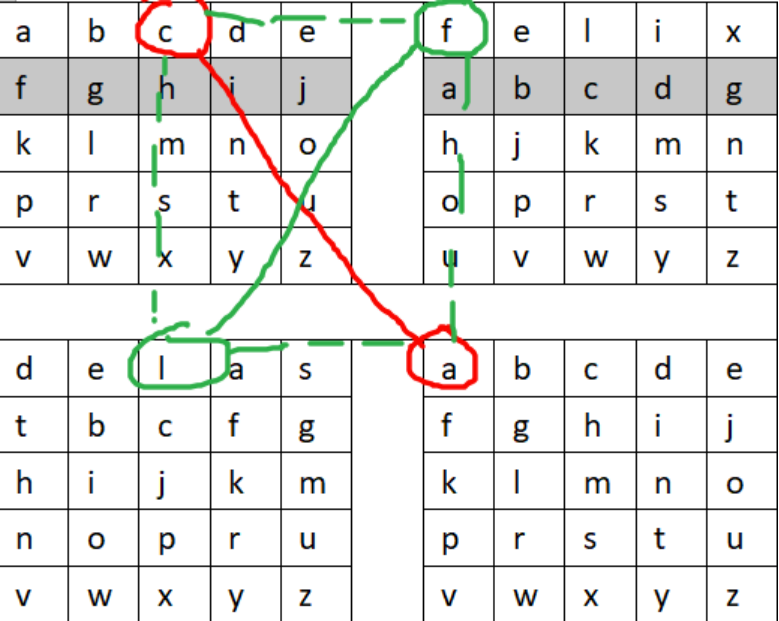
如上图,明文每两个字母为一组,找对照,ca对应fl,最后得到flagishere
Wp告诉我们要将其进行md5加密32位作为flag提交
数学大师
PolarD&N Crypto通关笔记 - baimi - 博客园
请直接查看他人的wp,本体使用到了sagemath,由于其他原因无法进行复现
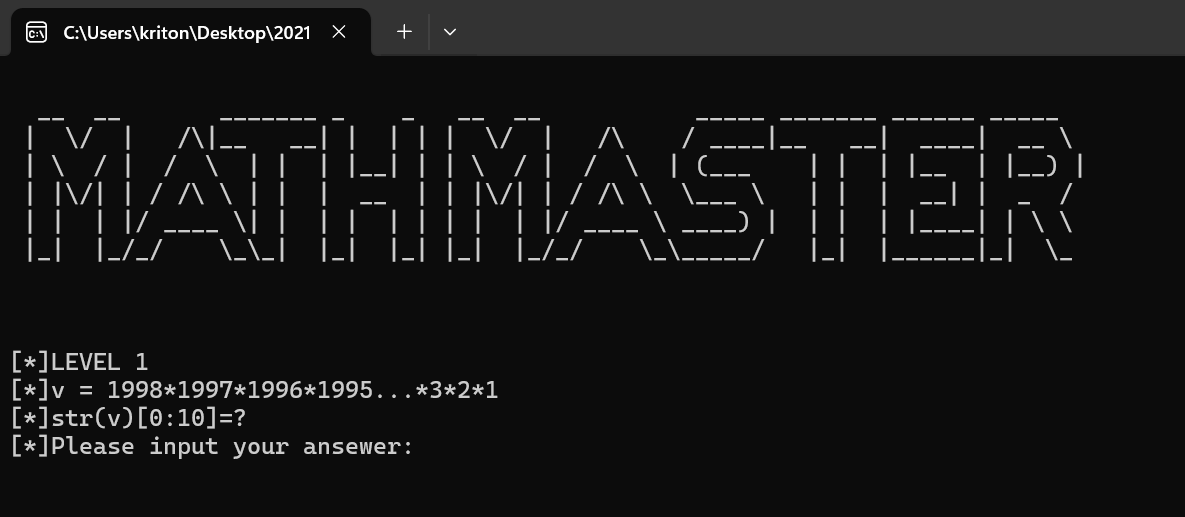
第一题是求1998阶乘,取前十位
8294835148
[*]LEVEL 2
[*]φ(718)=?
[*]hint:Euler's totient function
[*]Please input your ansewer:
欧拉函数,欧拉函数φ(N)表示小于或等于N的正整数中与N互质的数的个数。
在sage中求解欧拉函数可以用euler_phi(),可得 358
[*]LEVEL 3
[*]3*x+z-y=14,2*y+3*x-z=439,x+y+z=318
[*]x = :
三元一次方程组,解方程
x,y,z = var('x y z')
solve([3*x+z-y==14,2*y+3*x-z==439,x+y+z==318],x,y,z)
x=43,y=195,z=80,得到flag
flag{2381885c659b0eb108fe24c4297e5c04}
大主教的猪
大主教开的猪圈里的所有猪都不见了,你能帮大主教找到他们在哪吗?
hint:得到的结果小写套上flag{}提交。

变种猪圈密码

对照后得出的结果小写并用_连接后获得flag。
flag{they_are_on_the_truck}
玩转数独
(1,3,2,2)
(1,3,3,1)
(3,2,2,2)
(3,1,1,3)
(2,2,2,2)
(2,2,1,2)
(1,2,3,1)
(2,3,1,3)
(3,3,3,3)记得结果MD5小写套上flag{}哟~
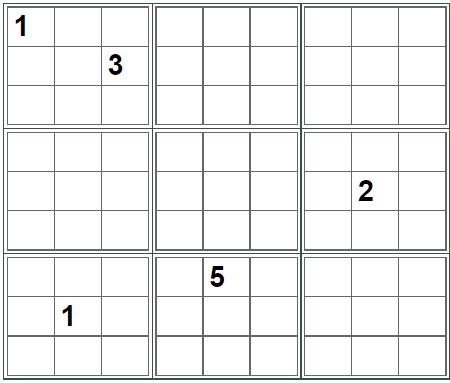
在线数独求解器
数独求解器 - 数独解题器 - 数独拍照解题器 - 9x9数独解答 - 九宫格数独解答
在线求解
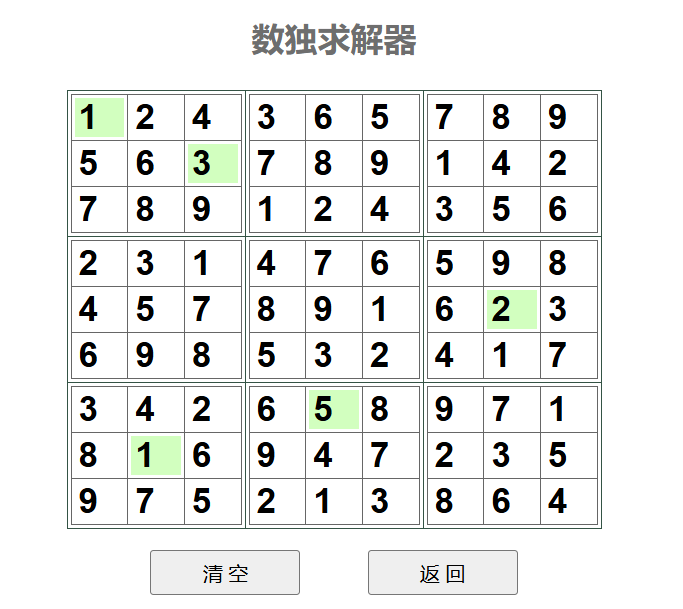
观察坐标,每组坐标有四个元素,但每个元素的范围都是在1-3,整体可以分成两个九宫格坐标系。一个大的,一个小的,如下图:
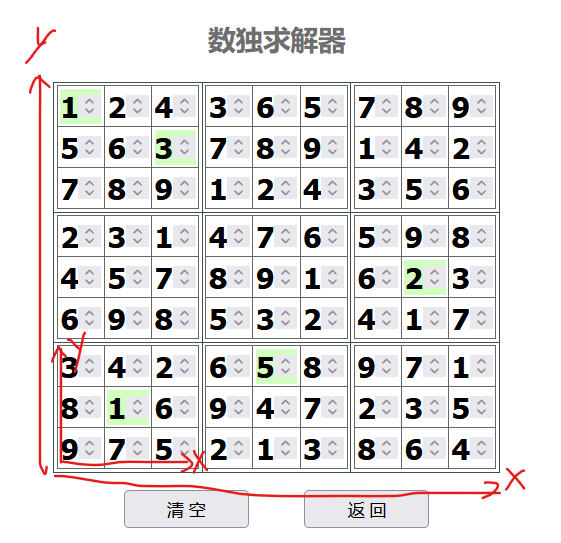
(1,3,2,2)对应的就是6,前两位对应大的,后两位对应小的。以此类推,得到的692998839。得到的结果32位MD5小写得到flag。
堂吉诃德走入猪圈
1.txt内容:
得到答案用MD532位小写加密套上flag{}
压缩包密码为数字

堂吉诃德分别对应” 678 5 56 67 “,找笔画?
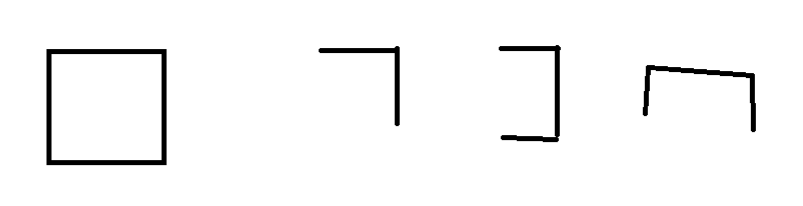
对应猪圈密码得到egdh,字母表数字排列,找到数字是5748,解压得到flag.txt
TIAMO
md5加密提交
flag{ccc49f40c1c0dd3c0f3bd7da83eb2643}
Round
得到两个txt文件
BRUEIFYRGBEUNVUICRHFU
FYURGUAROINNIEURYVYRU
E3BYUGDUWRNYUTFSRDE5W
FURYGRUTGUTUNAWGDUIEB
UYGIGNGIHFYBFYURGFURB
TFRUBYFUVOVNERTWINDUE
HUGRURBIGGNSUITIMTQEI
GBUTNGUIJTINGIEGFURYU
TYVCTYSAIBYEIFWIRHUGF
TRTUBGUYTRGSONIUONRRI
6YMUYTNYTIUWABRWBTESS
BRUHGUFGTJNUBAFDEGTEF
DHYEUBFYEYFTYUEBFIUBA
CTBRTNUKMIWGRBEHSDDVC
RUEBFUIRGFRBVXUAVTYEF
YUGRTFBUKCZUIWEIHUEFB
FRVRUIYUFRLNRUYGQEBYE
这里有两串密码,来找找flag在哪吧
(听说阿拉伯数字全世界通用哦)和谐民主和谐富强和谐民主和谐自由和谐富强和谐民主和谐自由和谐富强和谐文明和谐富强和谐民主和谐自由和谐富强和谐爱国和谐爱国和谐民主和谐富强和谐爱国
和谐爱国和谐自由和谐文明和谐民主和谐富强和谐民主和谐富强和谐爱国和谐爱国和谐自由和谐民主和谐富强和谐爱国和谐爱国和谐文明和谐富强和谐民主和谐富强和谐爱
国和谐爱国和谐自由和谐文明和谐富强和谐爱国和谐爱国和谐自由和谐文明和谐民主和谐富强和谐爱国和谐爱国和谐自由和谐文明和谐民主和谐富强和谐爱国和谐爱国和谐
自由和谐文明和谐民主和谐富强和谐爱国和谐爱国和谐自由和谐文明和谐民主和谐富强和谐爱国和谐爱国和谐自由和谐文明和谐民主lqbehgfdajmopcikn将找到的字符串进行md5加密后套上flag{}即可
先看熟悉的社会主义核心价值观解密
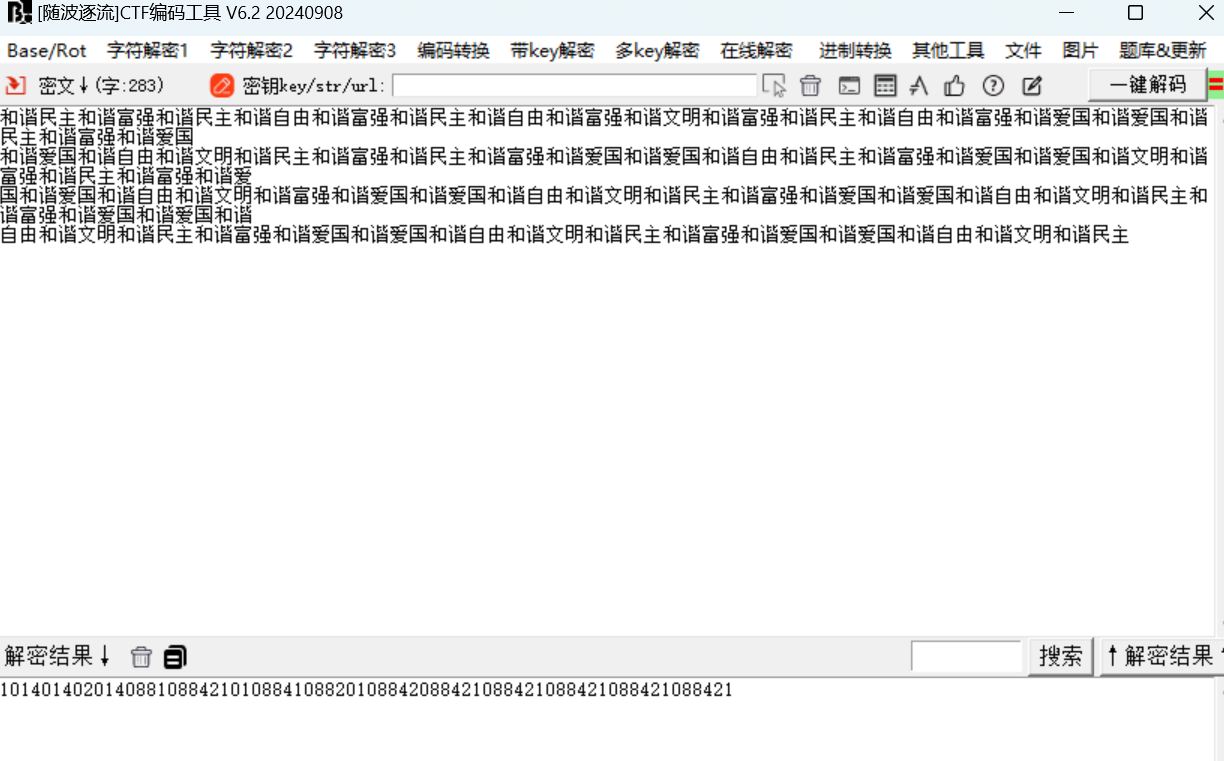
以0为间隔符,数字均为2的倍数,云影密码解密,得到AEEBEQWAURAVWWWWW
看了wp之后,原来到这里我拿到了密文c
剩下的TXT文本指的是托马斯杰斐逊 转轮密码
原理:给一个密码表,n行的26个字母,key是 1 - n 的数列, 密文是 n 个英文字母,根据 key 找对应行的密码表,然后在密码表上找密文字母,以这个字母为开头,重新排序。
先把lqbehgfdajmopcikn转成数字得到:12,17,2,5,8,7,6,4,1,10,13,15,16,3,9,11,14,密文是AEEBEQWAURAVWWWWW
比如第一个key是11,就要把第11行变为以A开头的串
6YMUYTNYTIUWABRWBTESS–>ABRWBTESS6YMUYTNYTIUW
以此类推
脚本如下:
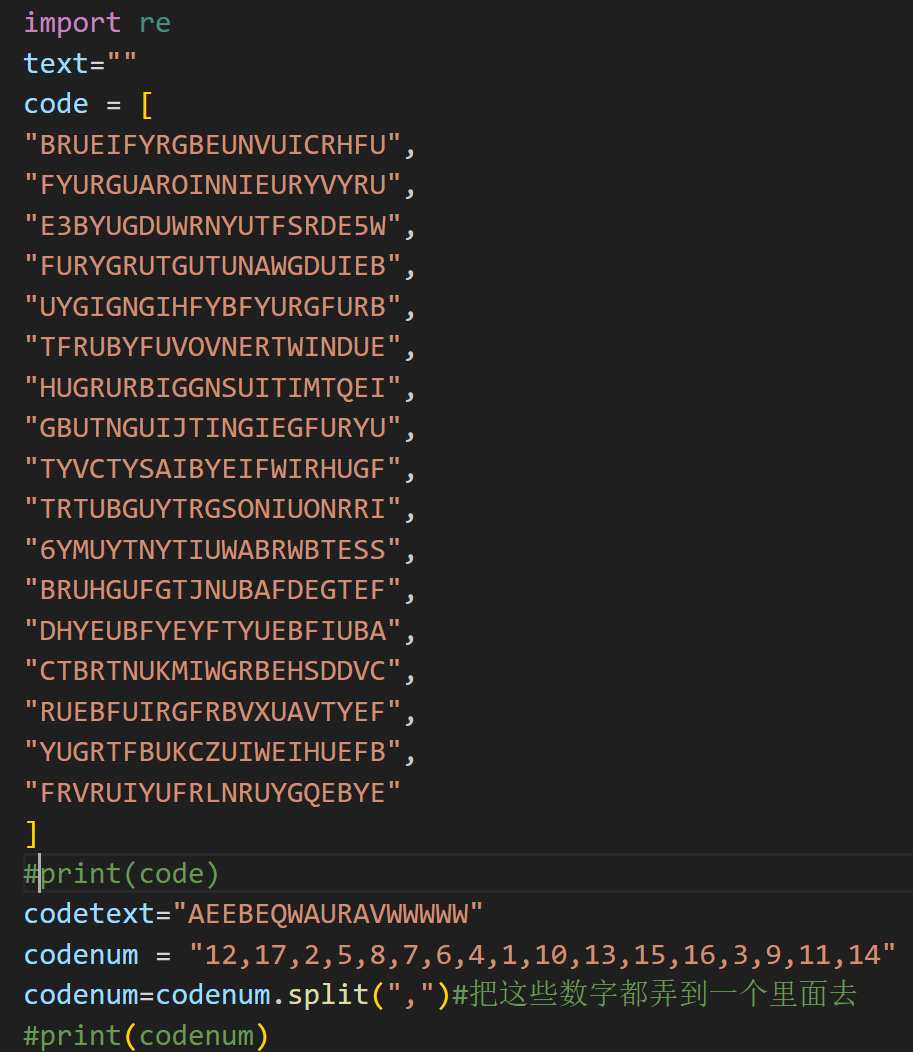
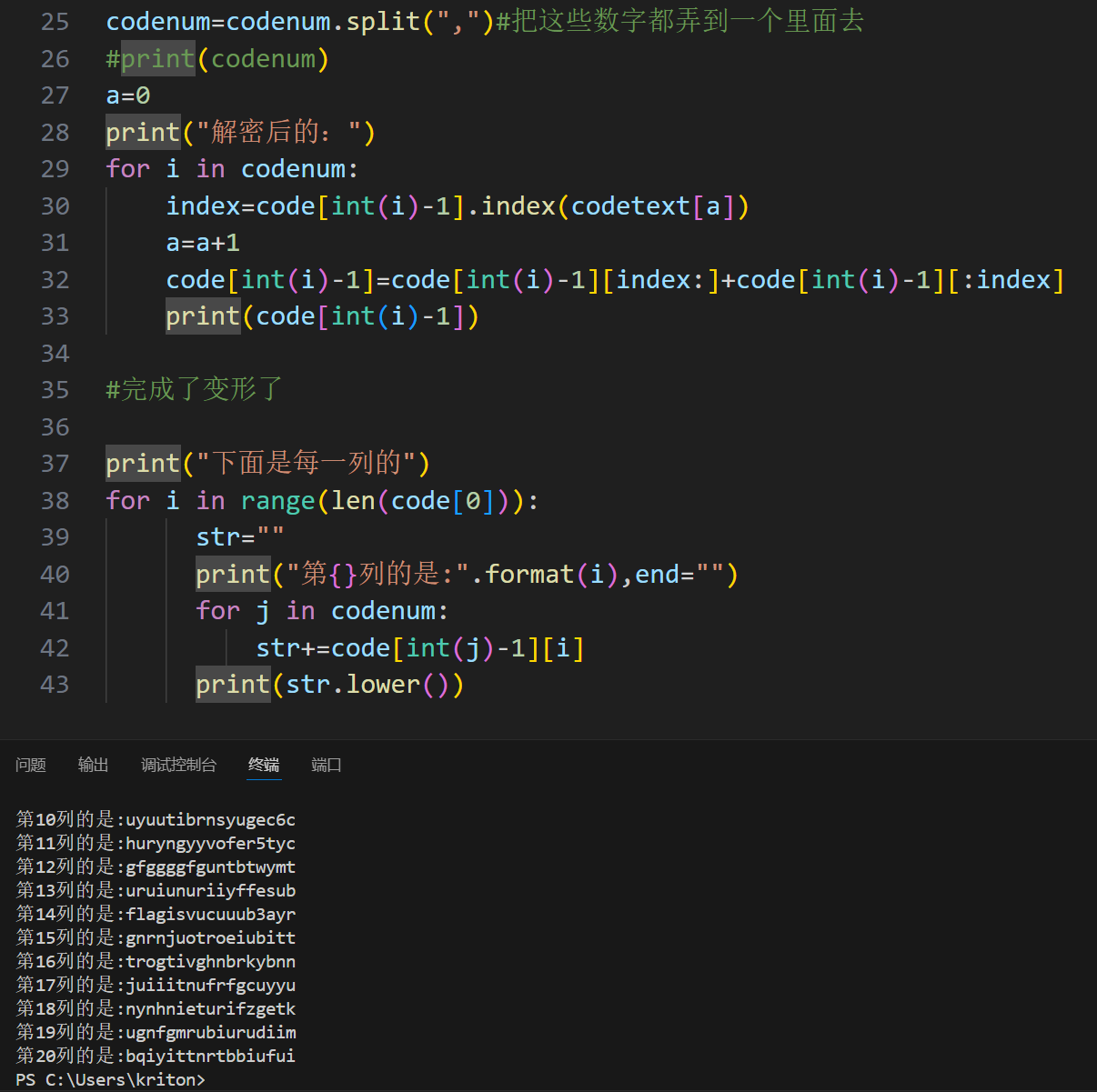
第十四列得到flag字符串,我们将其大写后进行MD5加密并提交
low encryption exponent RSA
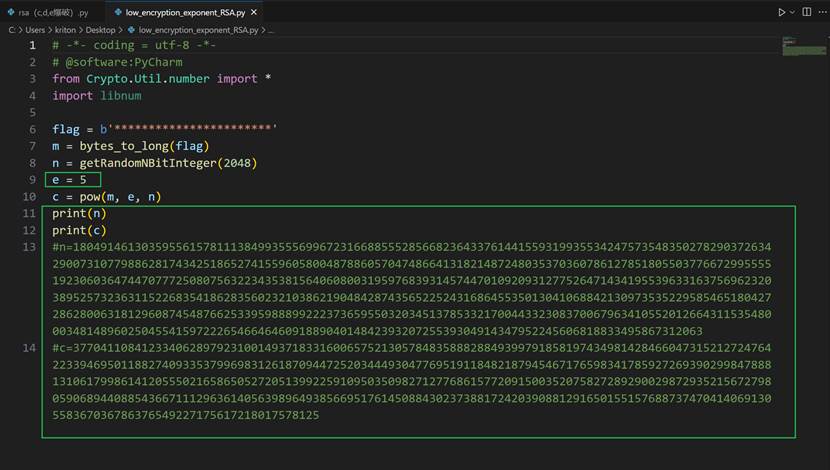
已知e,n,c,判断此为小e攻击
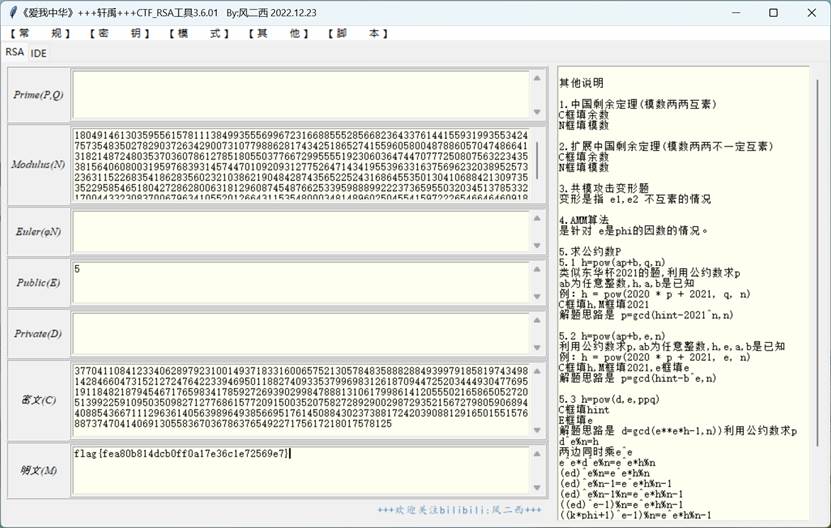
风二西的工具可轻易解得,模式选择即可
又或者使用低加密指数脚本解题,同样能够得到正确的flag
from gmpy2 import iroot
import libnum
e = 5
n = 18049146130359556157811138499355569967231668855528566823643376144155931993553424757354835027829037263429007310779886281743425186527415596058004878860570474866413182148724803537036078612785180550377667299555519230603647447077725080756322343538156406080031959768393145744701092093127752647143419553963316375696232038952573236311522683541862835602321038621904842874356522524316864553501304106884213097353522958546518042728628006318129608745487662533959888992223736595503203451378533217004433230837006796341055201266431153548000348148960250455415972226546646460918890401484239320725539304914347952245606818833495867312063
c = 377041108412334062897923100149371833160065752130578483588828849399791858197434981428466047315212724764223394695011882740933537996983126187094472520344493047769519118482187945467176598341785927269390299847888131061799861412055502165865052720513992259109503509827127768615772091500352075827289290029872935215672798059068944088543667111296361405639896493856695176145088430237388172420390881291650155157688737470414069130558367036786376549227175617218017578125k = 0
while 1:res = iroot(c+k*n,e) #c+k*n 开3次方根 能开3次方即可#print(res)if(res[1] == True):print(libnum.n2s(int(res[0]))) #转为字符串breakk=k+1
AFF
flag = "WMPTPTRGGPED"flaglist = []for i in flag:flaglist.append(ord(i)-97)flags = ""
for i in flaglist:for j in range(0,26):c = (3 * j - 17) % 26if(c == i):flags += chr(j+97)print(a,b,flag)
代码解释如下:
初始化:
flag = "WMPTPTRGGPED": 定义了一个需要解密的字符串。
flaglist = []: 初始化一个空列表,用于存储处理后的字符对应的数值。
字符到数值的转换:
遍历 flag 中的每个字符,将其 ASCII 值减去 97(即转换为小写字母相对于 'a' 的偏移量)。如果字符不是小写字母,这将导致非预期的负数或过大的正数,但在此代码中假设所有字符均为小写字母。解密过程:
初始化一个空字符串 flags,用于存储解密后的结果。
遍历 flaglist 中的每个数值 i。
使用一个内部循环遍历 0 到 25(即字母表中的 26 个字母),对于每个 j,计算 (3 * j - 17) % 26,这是一个典型的 Caesar 加密变种,但具有不同的系数和偏移量。
如果计算结果等于 i,则将 j 转换为对应的小写字母(通过 chr(j+97)),并添加到 flags 中。
这里得知了密文以及两个key值,分别是3,17
仿射密码解密
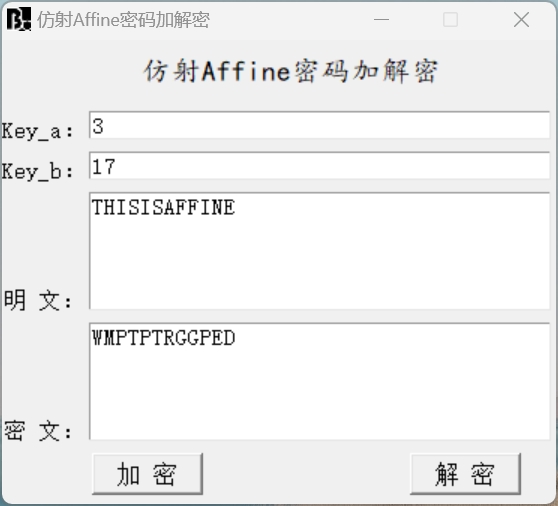
包上flag提交即可
base
j2rXjx8wSZjD
GHI3KLMNJOPQRSTUb=cdefghijklmnopWXYZ/12+406789VaqrstuvwxyzABCDEF5
ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz0123456789=+/
题目提示是base编码,文本第一行是密文,第二行是新的密码表,第三行是base64的密码表,考查的是base64换表
阴阳怪气的杰斐逊
通过题目得知,阴阳怪气编码和转轮密码
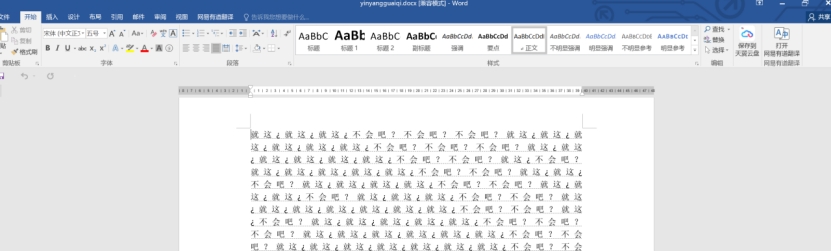

但是是隐藏的,这是因为我改了设置,让隐藏的自动显示

我们这里要让隐藏文字可复制
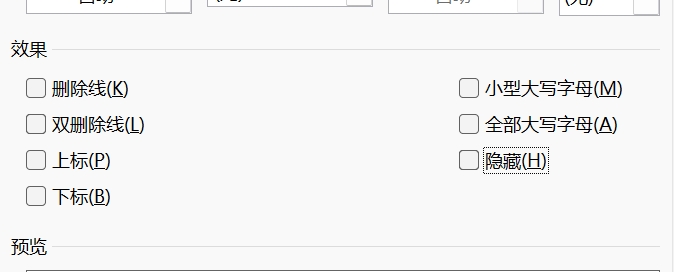
字体不勾选隐藏就可以了,开始解密
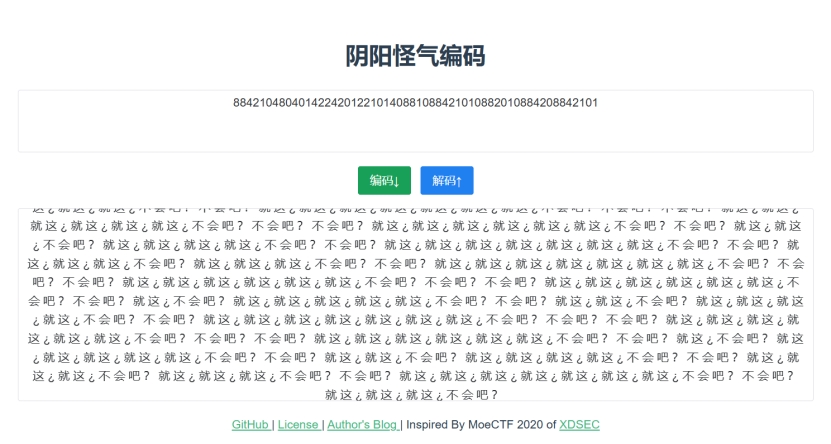
云影密码解密
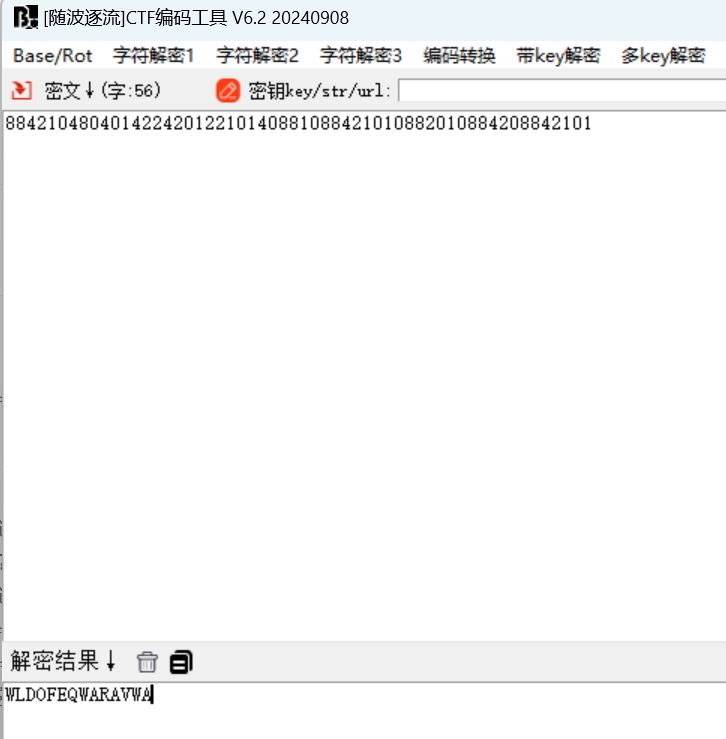
轮转密码解密
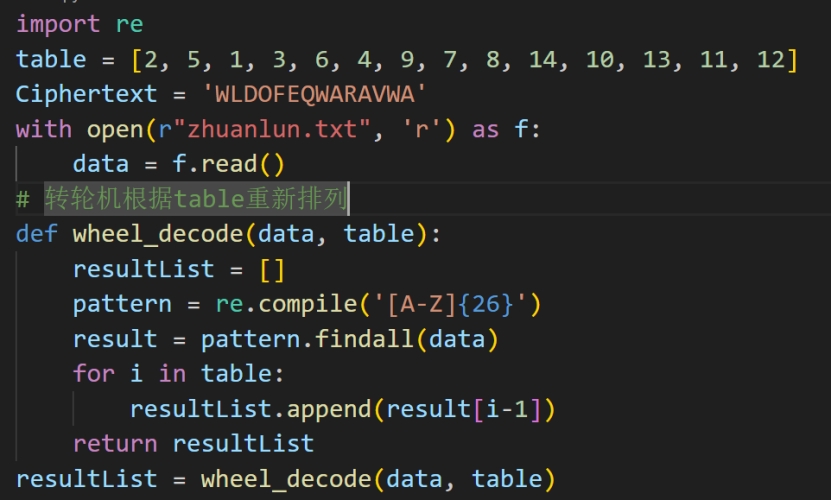
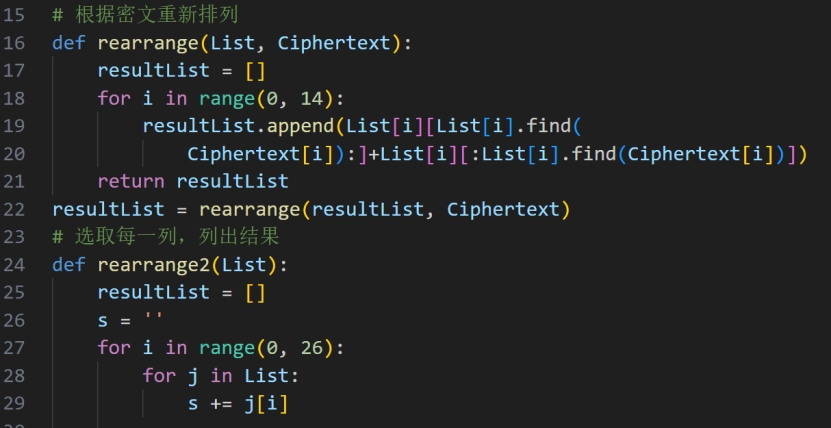
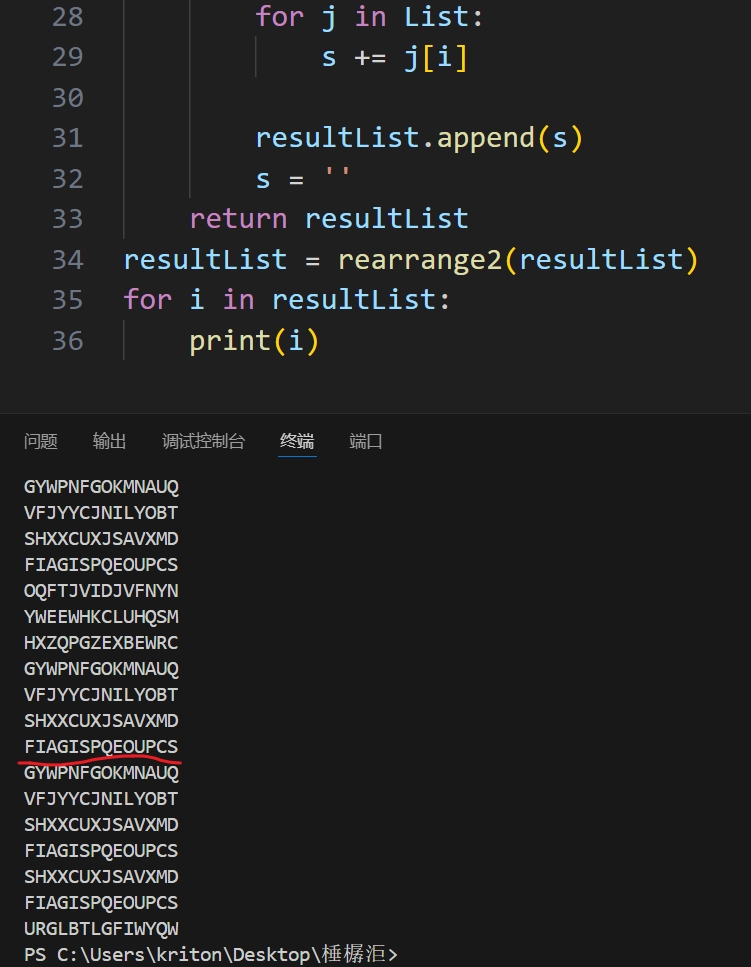
将其进行md5加密提交

KOBE的祝福短信
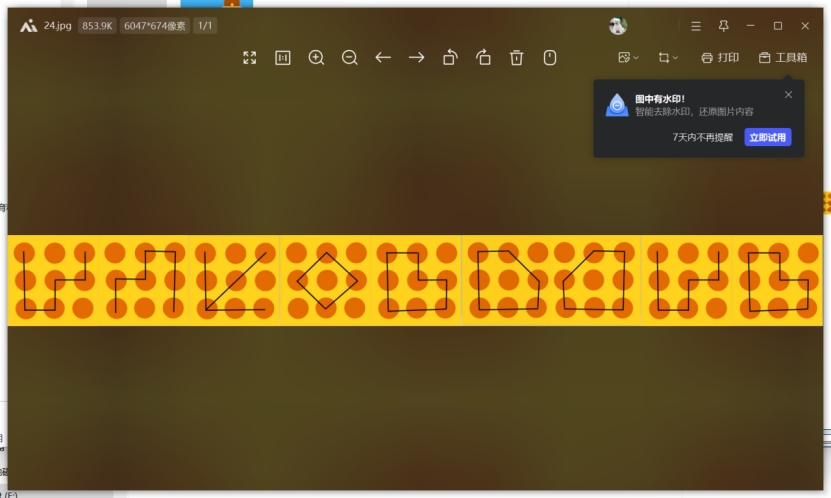
编码图如下

对照图片解码,得到压缩包密码NUMBERONE
之后再加密压缩包中得到9.txt,如图
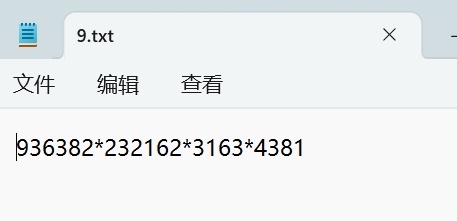
由提示以及题目中的"短信"可知解压得到的文本内容为九键加密,即每两位数字的前一位为第几个键,后一位为该键上第几个字母。按照这个方式将文本翻译后得到flag,根据提示全是小写套上flag{}即可。
小兔子的洋葱皮
TripleDES(BASE64(AES( flag{U2FsdGVkX1/pJiphUy6Qlf9WRoLg9kJPzHyBmk0SxAbWD7k/j97kG5kJTiahSaMK
GqNmYa8C0uZ7R3T0ccWj2/+HDWwe/qmL08+hjDKJD+o=} ) ) ) XOR ( key{U2FsdGVkX1+kBI+2EZDGEdeq} )
对flag三层套皮,洋葱皮拨开原来是指解密顺序是从外向里进行的,那么后面的key呢,原来是被rabbit加密过了
所以我们先解key
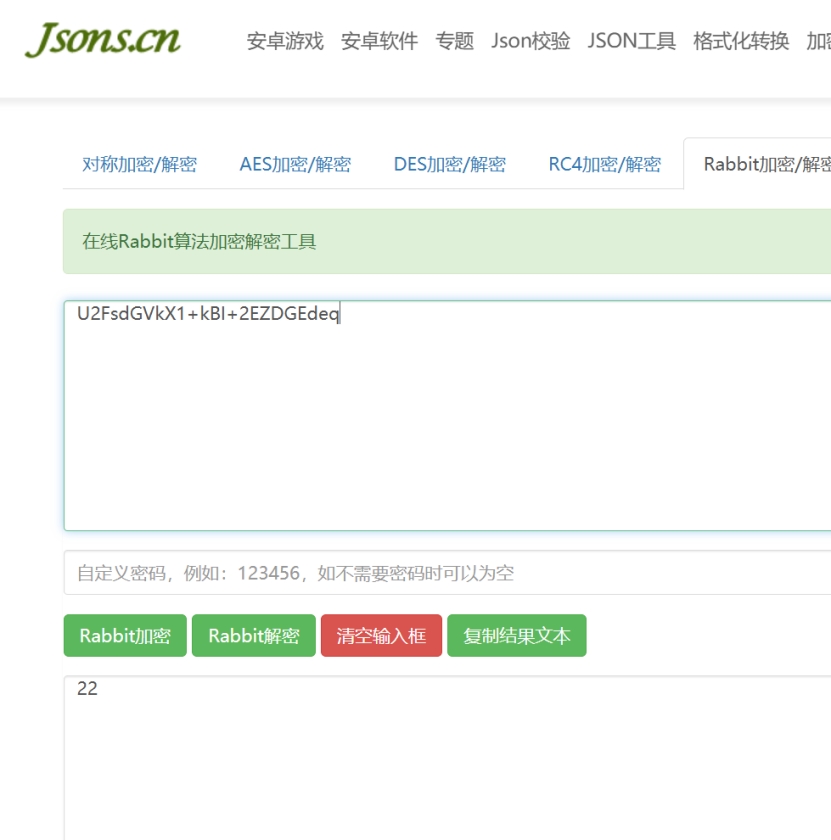
然后对flag进行剥皮
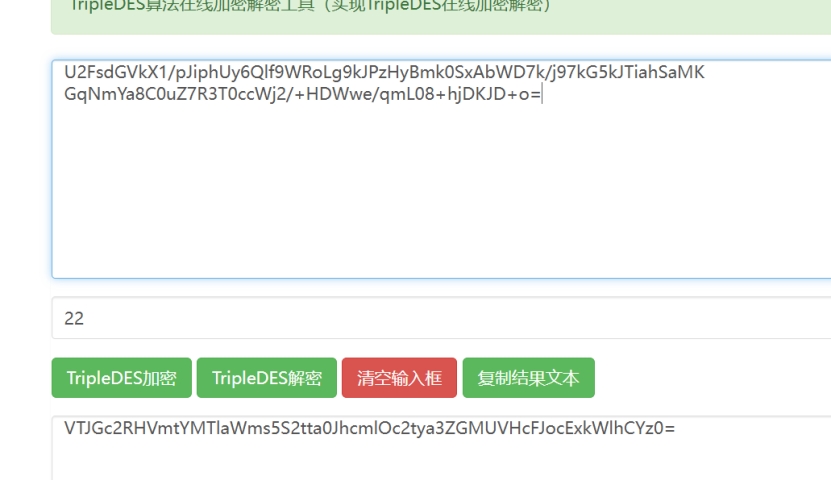
这里就需要填上key了
然后是base64解密
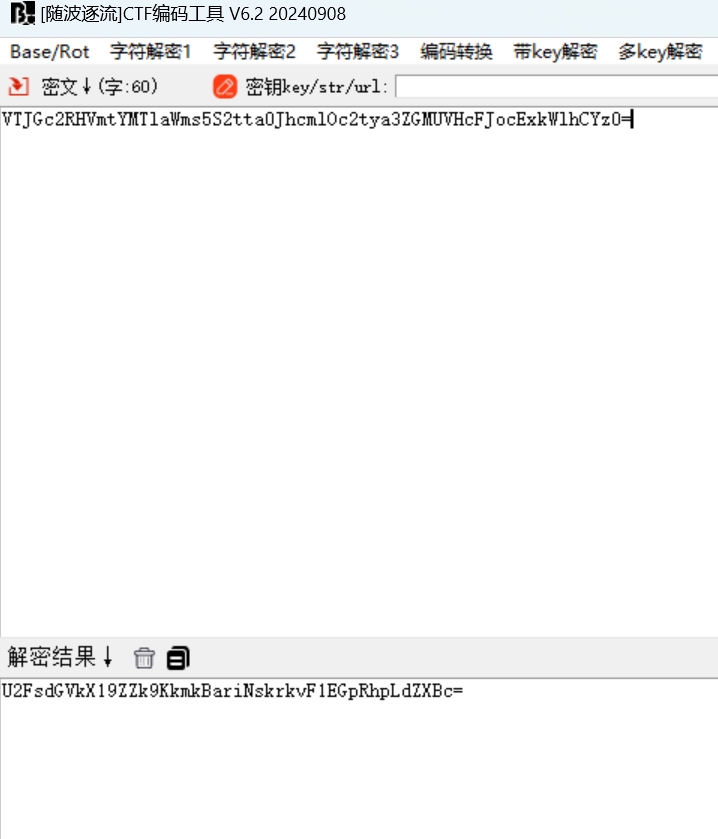
最后便是AES解密
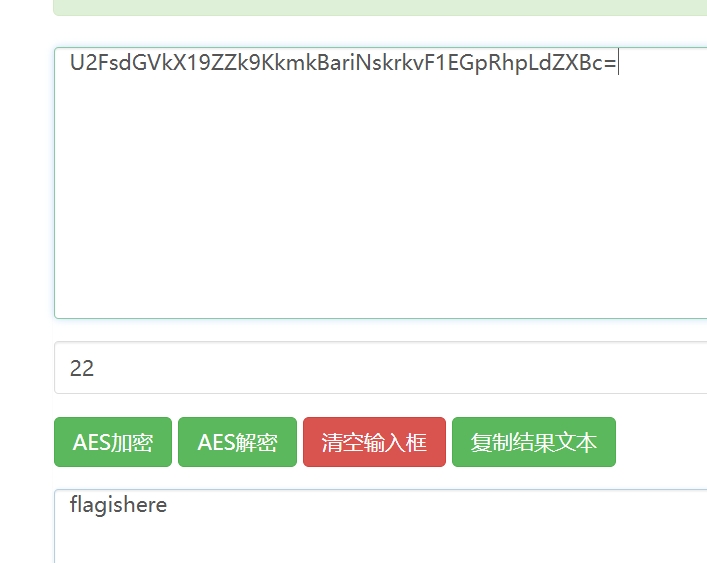

这个靶场的题都爱这样,最后要进行md5加密,包上flag即可
RSA密钥交换
小A的RSA
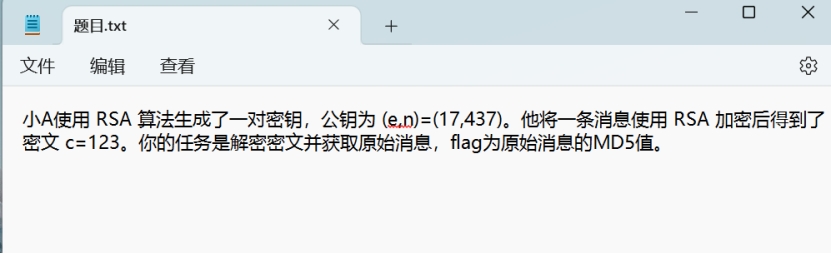
easyDES
RSA共模攻击
n1= 20367004933619640329031799226776514837061685981664854285308115632909435670724596920128402172098160576548639864098528644817516365660648152982472184401323785790562533467196556834124275893853534815001482876360398354954695792370636033673202145070244264275187457752956505832556854269231285319773348399301741813934834487846223229051935634443669493220012667872355681808618502449585839172939977649524262173256707695568263984472286856069995773192355643301872930251256460438128472182620887659172465881490174220827917135702261368000920219514539361766564775919476617752618166100973206718108473026971567131239107358379641923763013
n2= 20367004933619640329031799226776514837061685981664854285308115632909435670724596920128402172098160576548639864098528644817516365660648152982472184401323785790562533467196556834124275893853534815001482876360398354954695792370636033673202145070244264275187457752956505832556854269231285319773348399301741813934834487846223229051935634443669493220012667872355681808618502449585839172939977649524262173256707695568263984472286856069995773192355643301872930251256460438128472182620887659172465881490174220827917135702261368000920219514539361766564775919476617752618166100973206718108473026971567131239107358379641923763013
e1= 2333
e2= 23333
c1= 10264744066430466481593872630149143558573077174416980857009118692134660819073913212595308263898462327337283768644911383152506209840559778285757586705322364622425329621425100366723498923698716160356383331699930898455469318543849123623408889653265452565954257437198570129871082756267930336123137826093005304199337852991417533302939219968193861864872868938531890911844179764341487167273826185141101537209604030231278035081281820795150900579415774349854010257952836794529900536730723453110219127519437954530016383921843131179651083796172790701851004000889426375776340135273928938349542525459256006377475939436412482003970
c2= 5419945808600875685324905255766599302044490914532517430566320331248051121989090272712976205411073231922350575383585807837699039790705965844972602000549867253273355997765191642673804824094384527196797854210696722264604208353972695860473231983654542614752370002709975410103077627528638449599044074982480645065659196532121501525242050349677315892712735554820817806905097442560421171589689581990204756724213720035752010249253635380639611831099379821172339940499162281183608981563319912252895890992937277744761454652788338855099270346501953960046919430422924656133558212488023532963289949329182442150206387260469485512737
不互素的共模攻击
解题脚本如下(共两种):
import gmpy2
from Crypto.Util.number import *
n1= 20367004933619640329031799226776514837061685981664854285308115632909435670724596920128402172098160576548639864098528644817516365660648152982472184401323785790562533467196556834124275893853534815001482876360398354954695792370636033673202145070244264275187457752956505832556854269231285319773348399301741813934834487846223229051935634443669493220012667872355681808618502449585839172939977649524262173256707695568263984472286856069995773192355643301872930251256460438128472182620887659172465881490174220827917135702261368000920219514539361766564775919476617752618166100973206718108473026971567131239107358379641923763013
n2= 20367004933619640329031799226776514837061685981664854285308115632909435670724596920128402172098160576548639864098528644817516365660648152982472184401323785790562533467196556834124275893853534815001482876360398354954695792370636033673202145070244264275187457752956505832556854269231285319773348399301741813934834487846223229051935634443669493220012667872355681808618502449585839172939977649524262173256707695568263984472286856069995773192355643301872930251256460438128472182620887659172465881490174220827917135702261368000920219514539361766564775919476617752618166100973206718108473026971567131239107358379641923763013
e1= 2333
e2= 23333
c1= 10264744066430466481593872630149143558573077174416980857009118692134660819073913212595308263898462327337283768644911383152506209840559778285757586705322364622425329621425100366723498923698716160356383331699930898455469318543849123623408889653265452565954257437198570129871082756267930336123137826093005304199337852991417533302939219968193861864872868938531890911844179764341487167273826185141101537209604030231278035081281820795150900579415774349854010257952836794529900536730723453110219127519437954530016383921843131179651083796172790701851004000889426375776340135273928938349542525459256006377475939436412482003970
c2= 5419945808600875685324905255766599302044490914532517430566320331248051121989090272712976205411073231922350575383585807837699039790705965844972602000549867253273355997765191642673804824094384527196797854210696722264604208353972695860473231983654542614752370002709975410103077627528638449599044074982480645065659196532121501525242050349677315892712735554820817806905097442560421171589689581990204756724213720035752010249253635380639611831099379821172339940499162281183608981563319912252895890992937277744761454652788338855099270346501953960046919430422924656133558212488023532963289949329182442150206387260469485512737_,x,y=gmpy2.gcdext(e1,e2)
m=pow(c1,x,n1)*pow(c2,y,n2)%n1
a=gmpy2.gcd(e1,e2)
m=gmpy2.iroot(m,a)[0]
print(long_to_bytes(m))
from Crypto.Util.number import long_to_bytes
from gmpy2 import invert
def gongmogongji(n, c1, c2, e1, e2):def egcd(a, b):if b == 0:return a, 0else:x, y = egcd(b, a % b)return y, x - (a // b) * ys = egcd(e1, e2)s1 = s[0]s2 = s[1]if s1 < 0:s1 = - s1c1 = invert(c1, n)elif s2 < 0:s2 = - s2c2 = invert(c2, n)m = pow(c1, s1, n) * pow(c2, s2, n) % nreturn mn1= 20367004933619640329031799226776514837061685981664854285308115632909435670724596920128402172098160576548639864098528644817516365660648152982472184401323785790562533467196556834124275893853534815001482876360398354954695792370636033673202145070244264275187457752956505832556854269231285319773348399301741813934834487846223229051935634443669493220012667872355681808618502449585839172939977649524262173256707695568263984472286856069995773192355643301872930251256460438128472182620887659172465881490174220827917135702261368000920219514539361766564775919476617752618166100973206718108473026971567131239107358379641923763013
n2= 20367004933619640329031799226776514837061685981664854285308115632909435670724596920128402172098160576548639864098528644817516365660648152982472184401323785790562533467196556834124275893853534815001482876360398354954695792370636033673202145070244264275187457752956505832556854269231285319773348399301741813934834487846223229051935634443669493220012667872355681808618502449585839172939977649524262173256707695568263984472286856069995773192355643301872930251256460438128472182620887659172465881490174220827917135702261368000920219514539361766564775919476617752618166100973206718108473026971567131239107358379641923763013
e1= 2333
e2= 23333
message1= 10264744066430466481593872630149143558573077174416980857009118692134660819073913212595308263898462327337283768644911383152506209840559778285757586705322364622425329621425100366723498923698716160356383331699930898455469318543849123623408889653265452565954257437198570129871082756267930336123137826093005304199337852991417533302939219968193861864872868938531890911844179764341487167273826185141101537209604030231278035081281820795150900579415774349854010257952836794529900536730723453110219127519437954530016383921843131179651083796172790701851004000889426375776340135273928938349542525459256006377475939436412482003970
message2= 5419945808600875685324905255766599302044490914532517430566320331248051121989090272712976205411073231922350575383585807837699039790705965844972602000549867253273355997765191642673804824094384527196797854210696722264604208353972695860473231983654542614752370002709975410103077627528638449599044074982480645065659196532121501525242050349677315892712735554820817806905097442560421171589689581990204756724213720035752010249253635380639611831099379821172339940499162281183608981563319912252895890992937277744761454652788338855099270346501953960046919430422924656133558212488023532963289949329182442150206387260469485512737m=gongmogongji(n1,message1,message2,e1,e2)
print(long_to_bytes(m))
得到flag
flag{6480a3bf-82e2-44e0-9c32-b6a0da8ec46d}
variation-rsa
最后flag=(flag1+flag2+flag3)
variation_rsa.py就不展示了
解题脚本如下:
from Crypto.Util.number import *
import gmpy2c1 = 15586247697277532046812950432902773732327329184929961854997495210573627117260228709936327195953289907799735776425925363312137294734464930656006335287372431016600211951629567046779533236160645460268386728835983326093046904859159743244507215622807770074479759250929154791311227414122209325560728780689824290378441264308163115237261828259796271013473102073280513506976297605519870543598183104646977435546991722183887485579279535990826339444296156216087404614022283778959805361955256593072994347166395388701693394136294643451644783704090395347138731250701463174399456633197640174044073848759722308083678547686777162484795
c2 = 17538934691576368783671402501171847280494794600029573039793422483216151678595631267048878509399287917096434364875515741919976948438750360077454119679833636779683059708923187173534056993351622231730338590900612436146711101466447607660747846309349555660230127698911782175033934569458421302573395765698060907602063256600517663557182214450409111576326817516851471592870072454559230917774145790891005667612040640372734277924267234931622903586083603003276003081251200734229179424055785828132466558983095351212117320446426640092631710276126438840261800085306640721068097066410181192932853444970770042765344237745920213249599
c3 = 16500292460777375934245920298090466447118028191799066692857815637083078289925184090552039119465751284568237901897458018074018407946955502121238967064151893052235846218026798473133501871632705816383843633672282725382714026554688976046798940263992443021302540771543277815175625781564566057557112370221505148930784203175724847617881577039888356144680645030276155402270796992419421218599142459006125030744519466683717481511271970404369880716637102820401418219595824439631746538283450446161346732193660604974975033057222454482416413370442920846656168361120774965471969258033191477596029419991953860038094093086641087013952n1 = 14824267720565830614198366423536599666692078969408403530258418602151322644585576708517191288357418574410537646212589360867055238409644225020114747038342097744542022643037865665129552322573216047070677736725417436626920538199776045223182025555032687422098410274010072272948921387942284889428172227747124840681230287572405913777684484640035353309074356839921615363768839468380890923086904115913017609689750326299359077846457821010369130002914875100460359637094049091716624328545343429605828899486733904861746381542564902018804771429533804771098266001841458433664015729735822285137823715376774756745985491673136930276941
n2 = 21093893530165595850339636291340886775560459889174993298599564679470961520127537242137351793326916956073009495303622153882623912792088101281148271957920985536369095953335024370158909102755939425266322061024660469804331164229029302486833732919273709880115072578649082360889893770131535569945349586879686172801621707802368786052168013925892590355941771860436819249314675001571361991296570354259045254453585842424561844676250437625123809885279029491512960326206418322762119343167800501997630708987739950144724219375568233516957162796160222178022591375724806703162674485897117438453945303273004012532132059011075717387753
n3 = 18851781425565649500243914718895527060598553785142033499277947796047289729069551538151421839511239897691881228121437622923274745439286192958624933347473814433650645821240330239352230328910532686189064529002598986350545013596873280380093139589440286483854335646063005690269032198568724965964443111093291700142910652223408636268615176273268372177721667944316123253596652992256076572634227395015036348109972259736684061785035583511127926569341967394058493301139935304361924639075754092181040235419401702148068770694697982444290753353433701503833775179671108406498799549700127209151389161427718168658930877516526900193773
n4 = 24141384186719901100738328229558939321137195844627407412035205930880546126459260897433418685279927024995699136588216700770429628894224051287181657357533218989737870319139269421990248988961435374202640406264110282763206906390508271179764960952342404379846442988489435158217691170804372863828966379599925114485971708200189788312061335938149982724447336254731731196164294152411281627551943972751739099703406466680639123738668207648503911709799873188331259979032169198913999856215096219340617703116234922400948884716827963616800355410477122406692338452507358998811789750057925245184372948089354754021196407808558611706347
n5 = 27318577363188389010777000006309038146149568153342680277329454682460382014736977771701476436793256452622448296665625336293530182434223007914485160853928124259423931234549637565465312854050133553101056456348604117421250840812257865413145378087504121964973256347325500523801284199727074717327057009988590900033465488838411205419861719503492329750506421557659566793009179911321072512769094073583391850440926455889648811384353704831466087203207493141784030943780957637583967661055007939557364118592325819246060161116832663690401118085081185643994190287681118343291069123911734332419664019717764123106277592362757215369227
n6 = 23279048677948732944246045283025308427605697005872399005537528250552617144495344749322775508766281162164676817529480952526644219727544025172002421791418672728154203177554834465135080719871147878014347768357902201127620075363554533320943045725990456088670395831473286777889590888927822294580895334230380579965775406733741903354395281680491679994952638403650250478885893675153500100983994448967210657066830060805681453121007319883818996584537483756124030749688830761886047644923339363936836237308406534213706297507538286802906757352059469885515114285041899411525651842889457974296366733997911092037452209283086447745201e1 = 59537
e2 = 86311
e3 = 65537# 计算 q
p1=gmpy2.gcd(n1,n2)
p2=gmpy2.gcd(n3,n4)
p3=gmpy2.gcd(n5,n6)
# 计算 p
q1=n1//p1
q2=n2//p1
q3=n3//p2
q4=n4//p2
q5=n5//p3
q6=n6//p3phi1=(p1-1)*(q1-1)
phi2=(p1-1)*(q2-1)
phi3=(p2-1)*(q3-1)
phi4=(p2-1)*(q4-1)
phi5=(p3-1)*(q5-1)
phi6=(p3-1)*(q6-1)# 计算私钥
d1=gmpy2.invert(e1,phi1)
d2=gmpy2.invert(e1,phi2)
d3=gmpy2.invert(e2,phi3)
d4=gmpy2.invert(e2,phi4)
d5=gmpy2.invert(e3,phi5)
d6=gmpy2.invert(e3,phi6)m1=pow(c1,d2,n2)
m1=pow(m1,d1,n1)
print(long_to_bytes(m1).decode())
#把flag中的2给删了m2=pow(c2,d4,n4)
m2=pow(m2,d3,n3)
print(long_to_bytes(m2).decode())
#把flag中的5在原本位置上双写m3=pow(c3,d6,n6)
m3=pow(m3,d5,n5)
print(long_to_bytes(m3).decode())
#flag{c2c4c982b574fb735487899f11faed80}
最终经过修改得到flag
flag{cc4c98b5574fb7355487899f11faed80}