个人认为 B 和 C 质量都很高。
B
一个数轴上有 \(n\) 个炸弹,第 \(i\) 个炸弹位于 \(X_i\),爆炸半径为 \(R_i\),权值为 \(v_i\),这些炸弹的排布有两个性质:
-
若炸弹 \(x\) 可以直接或间接引爆炸弹 \(y\),那么 \(y\) 一定不能直接或间接引爆炸弹 \(x\)。
-
定义炸弹序列 \(a_1, a_2, \dots, a_k\) 要求 \(\forall i\in [1, k - 1]\),炸弹 \(a_i\) 可以引爆 \(a_{i + 1}\)。令 \(d(x, y)\) 为最大的 \(k\) 满足存在炸弹序列 \(a_1, a_2, \dots, a_k\) 且 \(a_1 = x, \ a_k = y\)。若 \(d(x, y) = 3\),则 \(x\) 一定可以直接引爆 \(y\)。
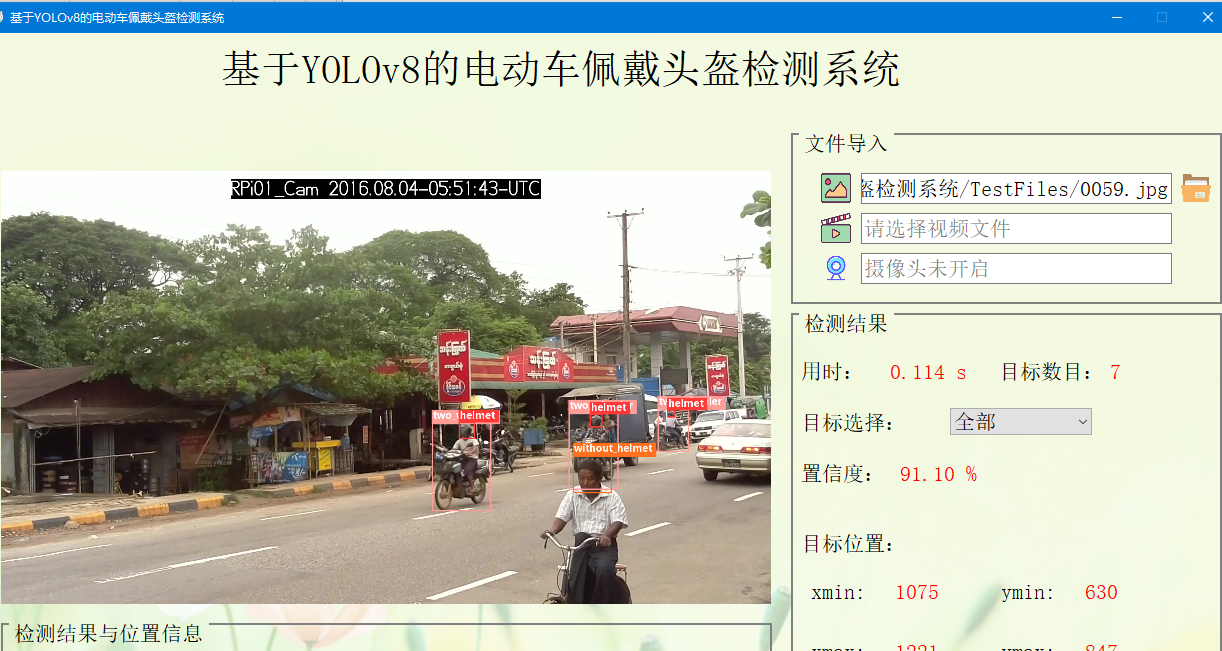
对于每个炸弹 \(i(1\le i\le n)\),求对于所有的炸弹序列 \(a_1, a_2, \dots, a_k\) 满足 \(a_k = i\),其 \(\sum\limits_{j = 1} ^ {k - 1} f(v_{a_j}, v_{a_{j + 1}})\) 的最大值,其中 \(f(u, v) = ((u\oplus v) + u\cdot v) \bmod 998244353\)。
\(1\le n\le 3\times 10^5, \ 0\le R_i\le 10^{18}, \ |X_i|\le 10^{18}\)
对于这种题,其代价函数 \(f(u, v)\) 几乎无法拆开,而且可能的转移数量为 \(\mathcal O(n ^ 2)\),那么算法几乎无法得到优化。
所以,关键点在于转移数量可能并不是 \(\mathcal O(n ^ 2)\)。
- Lemma:对于炸弹 \(x\),对于任意 \(k\ge 2\),炸弹 \(x\) 右边的满足 \(d(x, y) = k\) 的炸弹 \(y\) 至多一个。
Proof
反证。若存在 \(x, y, z\) 满足 \(X_x < X_y < X_z\) 且 \(d(x, y) = d(x, z) = k\)。
在炸弹 \(z\) 一路引爆到炸弹 \(x\) 的过程中同时会引爆炸弹 \(y\),那么 \(d(x, z) > d(x, y)\),矛盾。
- Theorem:\(\max\limits_{1\le x < y\le n} d(x, y) \le \mathcal O(\log R)\)。
Proof
考虑对于三个炸弹 \(x, y, z\) 满足 \(X_x < X_y < X_z\),若 \(z\) 可以直接引爆 \(y\),\(y\) 可以直接引爆 \(x\)。
由炸弹排布性质,\(z\) 可以直接引爆 \(x\)。
可得 \(X_y - X_x\le R_y,\ X_z - X_x\le R_z\)。
又知 \(y\) 不能引爆 \(z\),\(x\) 不能引爆 \(y\),那么 \(R_x < X_y - X_x, \ R_y < X_z - X_y\)。
所以 \(X_y - X_x \le R_y < X_z - X_y\),所以 \(R_x < X_y - X_x < \frac {X_z - X_x} 2 \le \frac {R_z} 2\)。
所以每引爆两个炸弹,半径至少减半,所以 \(d(x, y)\) 为 \(\mathcal O(\log R)\) 级别。