2024.12.13-26 北京集训-编程知识

2024.12.13-26 北京集训

news/2024/12/28 21:57:06/文章来源:https://www.cnblogs.com/Tmbcan/p/18638024

Day1

没学新东西，写了一天题。

模拟赛：
T1：
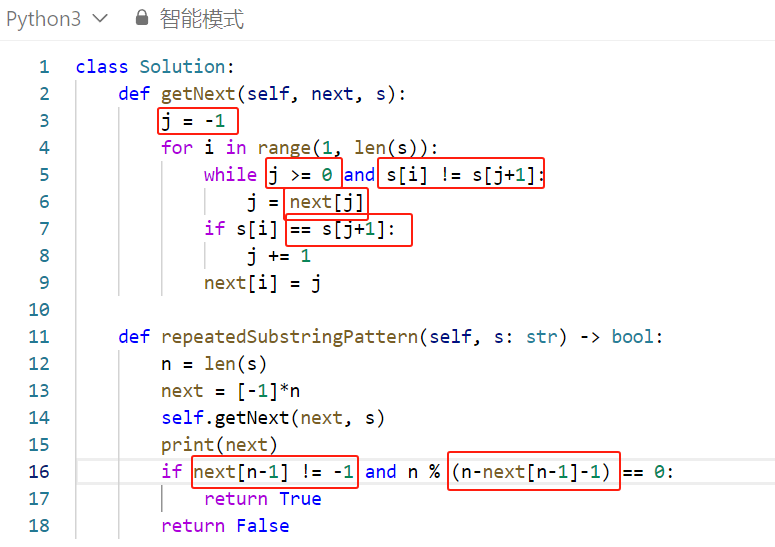
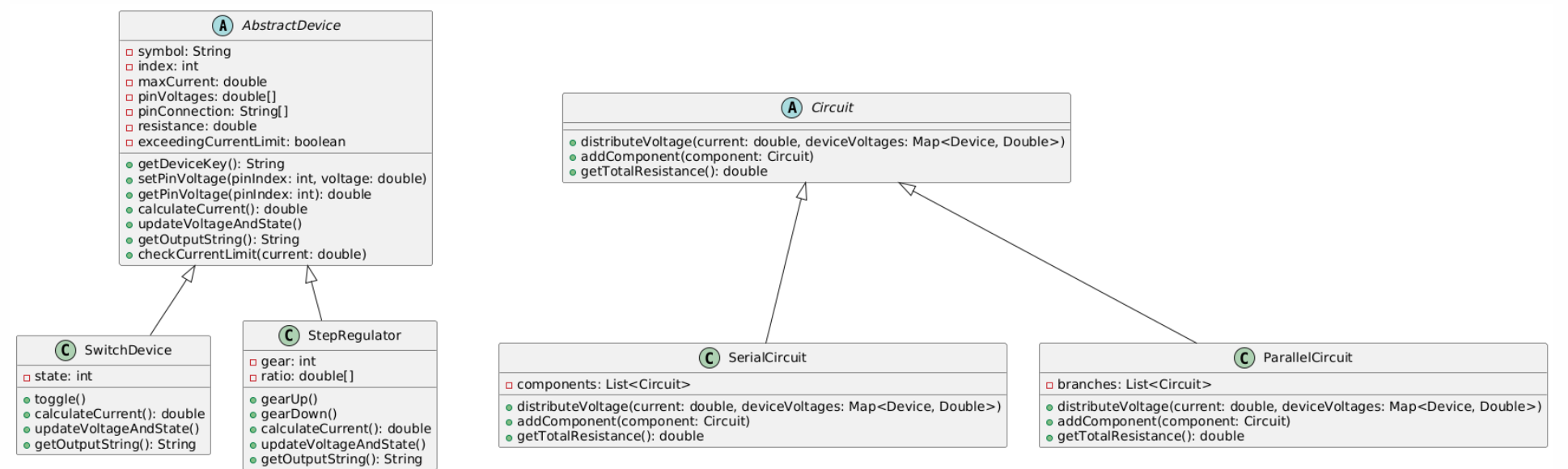
可以花费 \(k_1\) 代价令 \(x+=k_1!\)，花费 \(k_2\) 代价令 \(x+=2^{k_2}\)，初始时 \(x=0\)，求令 \(x=m\) 的最小代价。\(m\le1e12\)。
发现操作一做多执行 \(15\) 次，枚举要进行几次操作一，剩下的 \(m-x'\) 二进制拆分即可。

T2：
给定一个序列 \(A_n\)，构造一个 \(n\) 个点 \(m\) 条边的无向图，使得其 \(DFS\) 序恰为 \(A_n\)。求所有构造方案中，每个节点到根节点 \(1\) 的最大值最小为多少。
考虑按照序列分层进行构造，贪心地在每层中增加节点即可。

T3：
给定一个序列，支持区间加、减、乘、除以 \(2\) 操作，且除法最多 \(60\) 次，查询单点的奇偶性。\(n\le3e5,-1e9\le k\le1e9\)。
由于除法操作很少，所以线段树只需维护每个数的后 \(60\) 位即可，每次暴力进行除法。
自己场上进行了势能分析，但由于取模而导致挂分，但是本题数据是脚造的，不去管 \(k\le1e9\) 可以直接通过本题。

T4：
给定一个序列，可以涂三种颜色，要求相邻颜色不同，且每种颜色需涂 \(k_1\)、\(k_2\)、\(k_3\) 种，求涂色方案数。
考虑 \(dp\)，组合数压缩转移路径。

DAY2

主要学习模拟退火，是一种随机化算法，详见 PDF。
学了几个新的二分哈希答案思路，深受震撼。

DAY3

树剖、Dsu on Tree、平衡树。

DAY4

主要学习分层图和同余最短路。写了点题。

模拟赛：
T1：
求序列所有子区间的不同 \(GCD\) 的个数，\(a_i\le100,n\le1e5\)。
直接枚举 \(Gcd\)，从当前枚举 \(Gcd\) 的倍数开始查找区间，区间越长一定不劣，贪心地覆盖每个区间即可。

T2：
一个人初始时在数轴原点，向左走概率为 \(p\)，向右走概率为 \(q\)，求走 \(n\) 时到达过了 \(m\) 的概率，\(n\le1e7\)。
当 \(n\le1000\) 时，\(n^2\) \(dp\) 即可。
当 \(n\le1e7\) 时，考虑将数轴上走路扔到二维平面上，发现到达过 \(m\) 点当且仅当所走路线经过过 \(f(x)=(x-m)\)。考虑容斥，用卡特兰数计算不可行的方案数即可。

T3：
求给定矩阵的所有矩阵的 \(k\) 次方和，\(m\le n \le1e5\)。
首先考虑 \(m=1\) 的情况，二项式定理化简即可。
\(m=2\) 时，对原前缀和数组进行二维前缀和，再次二项式定理化简。
推广至 \(m=k\)，\(\sqrt{n}\) 枚举矩形左右边界，预处理出后缀和，对答案进行前缀和二项式定理拆解即可。

T4：
给定一个序列，支持单点修改，询问 \(L\) 到 \(R\) 中有多少长度为 \(K\) 的区间满足 \(\forall i,j(i\ne j),gcd(i,j)\ne 1\)。
把所有数分解质因数，区间内有相同质因数时才会存在数字不互质，有 \(set\) 维护即可。
将将修改操作看作线段树上区间加减一，每次查询区间连续 \(0\) 的个数即可。

DAY5-DAY6

DP 专题，学傻了。

DAY7

概率期望。

所有期望问题都可以转化为计数问题。

模拟赛：
T1：
给定 \(m\) 个序列的第一项，每个序列具有相同的递推关系，将 \(m\) 个序列按字典序排序，\(m\le1e6\)。
简单排序即可。

T2：
给定一个序列，支持区间 \(L\sim R\)，中每个数加 \(F_{i-L+1}\)，\(F_n\) 为斐波那契数列，查询区间和，\(n\le1e6\)。
考虑斐波那契数列的性质，斐波那契数列分类及合并后一定也是一个类斐波那契数列，所以可以在线段树上维护。
维护每个节点上类斐波那契数列的首项、项数即可。

T3：
给定一个序列，在其中选 \(m\) 个互不相邻的元素，使选出的元素总的极差最小，求最小极差，\(n\le1e5\)。
二分极差的值，枚举最小值就可以求出最大值，由最大最小值贪心的向两边选元素。
将处于最大最小值之间的数看作 \(1\)，其余看作 \(0\)，每次检查答案合法性时，转换为求序列上连续 \(1\) 的个数，线段树维护即可。

T4：
给定序列 \(A_n\)，定义 \(f(l,r)\)。若 \(1\le i \le n,l\le a_i\le r\)，则 \(f(l,r)=1\)。支持单点修改，求 \(\sum_{1\le l\le r\le n} f(l,r)\)，\(n\le 2e5\)。
考虑修改时，会对 \(f\) 的若干个后缀产生影响。具体产生哪些影响，需要看 \(A_{l,r}\) 中比当前区间大或小的数的个数及其位置。
用两个单调栈维护受影响的位置，线段树维护答案即可。