2 方差分析
2.1 单因素方差分析
2.1.1 分析基础
若控制变量有k个水平,不同水平下各观测变量的总体均值记为μ1,μ2,…,μk,则单因素方差分析的原假设为μ1 = μ2 = … = μk,即各总体均值都相等。
单因素方差分析认为,观测变量值的变动受到控制变量和随机变量两方面的影响。据此,可将观测变量总的离差平方和分解为组间离差平方和(between groups)与组内离差平方和两部分。
数学表述为
其中,
SST(sum square of total)为观测变量的离差平方和;
SSA(sum square of factor A)为组间离差平方和,是控制变量的不同水平造成的变差;
SSE(sum square of error)为组内离差平方和,是抽样误差引起的变差。
SST的数学定义为
其中,
k为控制变量的水平数;
$ x_{ij}\(为控制变量第i个水平下的第j个观测值;
\) n_i\(为控制变量第i个水平下的样本量;
\) \bar{x}$为观测变量均值。
SSA的数学定义为
其中,
$ \bar{x}_i$为控制变量第i个水平下观测变量的样本均值。
可见,组间离差平方和是各水平均值与总均值离差的平方和,反映了控制变量不同水平对观测变量的影响。
SSE的数学定义为
可见,组内离差平方和是每个观测值与本水平均值离差的平方和,反映了抽样误差的大小。
进一步,单因素方差分析研究SST与SSA和SSE的大小比例关系。
容易理解,在观测变量总离差平方和中,如果组间离差平方和相对于组内离差平方和较大,则说明观测变量的变动主要由控制变量引起,可由控制变量来解释,控制变量对观测变量造成了显著影响,与观测变量相关;反之,则不相关。
2.1.2 F统计量
基于上述考虑,单因素方差分析的检验统计量是F统计量,数学定义为:
其中,
n为总样本量;
k - 1和n - k分别为SSA和SSE的自由度;
MSA是组间离差平方和的平均,即组间方差;
MSE是组内离差平方和的平均,即组内方差。
F统计量有效地消除了水平数和样本量对分析造成的影响。
原假设成立条件下,F统计量服从自由度为(k - 1, n - k)的F分布。
将相关数据代入后可计算出F统计量的观测值和概率p值。
-
如果控制变量对观测变量造成了显著影响,则在观测变量总的变差中控制变量的影响所占的比例相对随机因素必然较大,F值显著大于1;
-
如果控制变量没有对观测变量造成显著影响,则观测变量的变差应归结为由随机因素造成,F值接近1。
当给定显著性水平α后,如果概率p值小于显著性水平α,则应拒绝原假设,认为控制变量不同水平下观测变量各总体的均值存在显著差异,控制变量的不同水平对观测变量产生了显著影响,与观测变量相关;反之,如果概率p值大于显著性水平α,则不应拒绝原假设,认为控制变量不同水平下观测变量各总体的均值无显著差异,控制变量的不同水平对观测变量没有产生显著影响,与观测变量不相关。
2.1.3 数学模型
设控制变量\(A\)有\(k\)个水平,每个水平均有\(r\)个样本(\(r\)次试验)。
那么,在水平\(A_{i}\)下的第\(j\)次试验的观测值\(x_{ij}\)可定义为
其中,
\(\mu_{i}\)为观测变量在水平\(A_{i}\)下的期望均值;
\(\varepsilon_{ij}\)为抽样误差,是服从正态分布\(N(0,\sigma^{2})\)的随机变量。
如果令
\(\mu\)为观测变量总的期望均值,且令
则\(a_{i}\)是控制变量水平\(A_{i}\)对观测变量产生的附加影响,称为水平\(A_{i}\)对观测变量产生的效应,且
对\(a_{i}=\mu_{i}-\mu\)作变换,并将其代入
则有
即为单因素方差分析的数学模型。
可见,单因素方差分析的数学模型为线性模型。\(\mu\)的无偏估计\(\hat{\mu}=\bar{x}\),\(a_{i}\)的无偏估计\(\hat{a}_{i}=\bar{x}_{i}-\bar{x}\)。
如果控制变量\(A\)对观测变量没有影响,则各水平的效应\(a_{i}\)应全部为\(0\),否则应不全为\(0\)。
单因素方差分析正是要对控制变量\(A\)的所有效应是否同时为\(0\)进行推断。
2.1.4 R语言函数
实现单因素方差分析的R函数为aov,基本书写格式为:
aov(观测变量域名~控制变量域名,data = 数据框名)
其中,数据组织在data指定的数据框中;控制变量应为因子。
aov函数默认输出组间离差平方和、组内离差平方和,以及各自的自由度。
若要得到包含检验统计量F的观测值、概率p值等更多信息的方差分析表,则需进一步调用summary函数或anova函数。
anova函数的基本书写格式为:
anova(方差分析结果对象名)
2.15 案例分析
有不同年份的13种汽车车型的相关指标数据398条。
① 变量包括:汽车在城市道路上每加仑汽油可行驶的公里数(MPG)、气缸数(cylinders)、排气量(displacement,单位:立方英寸)、发动机马力(horsepower)、自重(weight,单位:磅)、加速时间(acceleration)、车型(ModelYear)、原产地(origin)。
现需根据观测样本,检验不同年份车型的MPG总体均值是否存在显著差异?
###单因素方差分析
CarData<-read.table(file="CarData.txt",header=TRUE)
CarData$ModelYear<-as.factor(CarData$ModelYear)
aov(MPG~ModelYear,data=CarData)
OneWay<-aov(MPG~ModelYear,data=CarData)
anova(OneWay)
summary(OneWay)
结果
Call:aov(formula = MPG ~ ModelYear, data = CarData)Terms:ModelYear Residuals
Sum of Squares 10401.78 13850.79
Deg. of Freedom 12 385Residual standard error: 5.998007
Estimated effects may be unbalanced
OneWay<-aov(MPG~ModelYear,data=CarData)
anova(OneWay)
结果
| Df | Sum Sq | Mean Sq | F value | Pr(>F) | |
|---|---|---|---|---|---|
| ModelYear | 12 | 10401.78 | 866.81524 | 24.09421 | 5.264017e-40 |
| Residuals | 385 | 13850.79 | 35.97608 | NA | NA |
summary(OneWay)
Df Sum Sq Mean Sq F value Pr(>F)
ModelYear 12 10402 866.8 24.09 <2e-16 ***
Residuals 385 13851 36.0
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
附录B: python代码
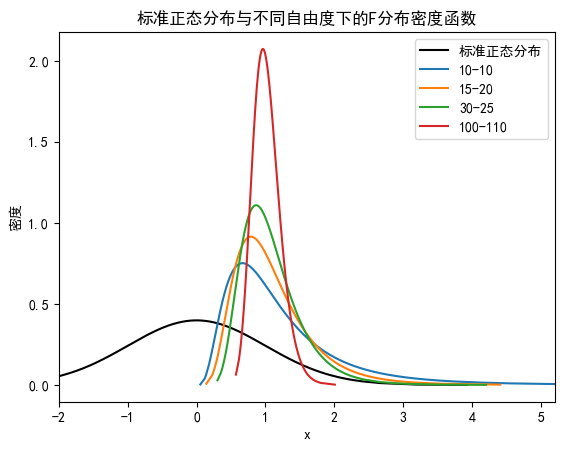
B.1 正态分布vs F分布
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import f, normimport matplotlib as mpl# 设置中文字体
mpl.rcParams['font.sans-serif'] = ['SimHei'] # 指定中文字体为 SimHei
mpl.rcParams['axes.unicode_minus'] = False # 解决负号显示问题# 设置随机种子
np.random.seed(12345)# 生成标准正态分布的随机数
x = np.random.normal(0, 1, 1000)# 对随机数进行排序
x.sort()# 计算标准正态分布的概率密度函数
y = norm.pdf(x, 0, 1)# 绘制标准正态分布的概率密度函数
plt.plot(x, y, label='标准正态分布', lw=1.5,c='black')# 不同自由度的F分布
df1 = [10, 15, 30, 100]
df2 = [10, 20, 25, 110]# 绘制不同自由度的F分布的概率密度函数
for i in range(4):x = f.rvs(df1[i], df2[i], size=1000)x.sort()y = f.pdf(x, df1[i], df2[i])plt.plot(x, y, label=f'{df1[i]}-{df2[i]}')# 添加图例
plt.legend()# 设置图表标题和坐标轴标签
plt.title(r'标准正态分布与不同自由度下的F分布密度函数')
plt.xlabel('x')
plt.ylabel('密度')# 设置横轴刻度范围
plt.xlim(-2, 5.2)# 显示图表
plt.show()