线段树详介(带lazy)
线段树和树状数组不同,它维护的是一个个子序列。
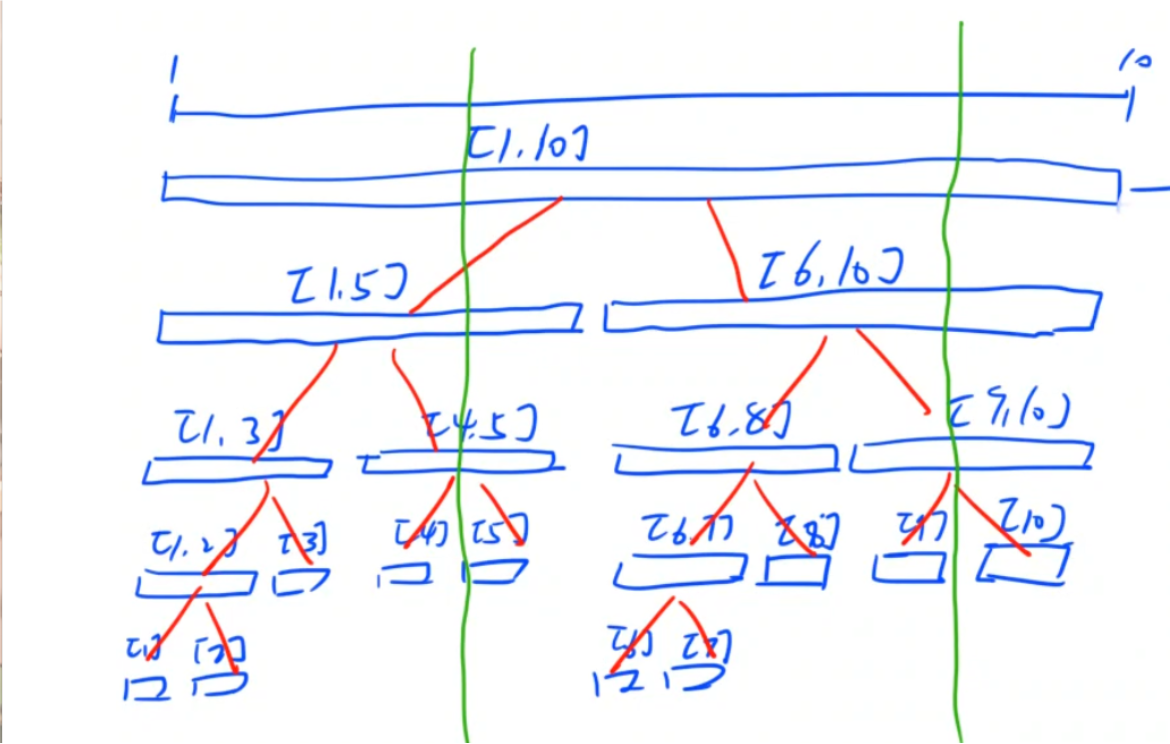
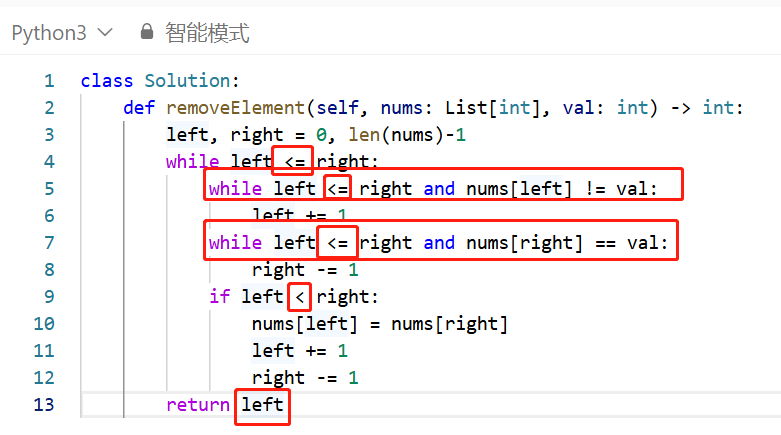
如上图,对于一个区间 \([l, r]\),它的左儿子就是 \([l, mid]\),右儿子就是 \([mid + 1, r]\),其中 \(mid = \frac{l+r}{2}\)。
我们可以给线段树上的每一个结点编号,假设父节点编号为 \(x\),左儿子编号就是 \(x\times2\),右儿子编号就是 \(x\times2+1\)。
struct Stree {int l, r, v;
} tr[N * 4];
以上代码是最简单的线段树,其中 \(l, r\) 为区间的左右端点,\(v\) 为区间内所有数的最大值。
然后我们来说如何维护线段树。
首先,建树。
我们可以参照上图,我们从根节点开始,每次分别递归左儿子和右儿子,直到叶节点。此时它的最大值就应该是它本身。然后我们回溯到父节点,由于我们已经对它的儿子都做过了,所以我们可以用儿子的值求出父亲,即父亲的最大值可以通过儿子的最大值推出来。
void pushup(int u) {tr[u].v = max(tr[u << 1].v, tr[u << 1 | 1].v);
}
void build(int u, int l, int r) {tr[u].l = l, tr[u].r = r;if (l == r) return;int mid = l + r >> 1;build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);pushup(u);
}build(1, 1, n);
以上代码中,\(build\) 就是建树,\(pushup\) 就是用儿子来更新父亲。
有的时候我们可能会这样写 \(build\)。
void build(int u, int l, int r) {if (l == r) tr[u] = {l, r, w[r]};else {int mid = l + r >> 1;tr[u] = {l, r};build(u << 1, l, mid); build(u << 1 | 1, mid + 1, r);pushup(u);}
}
此时请注意 \(else\) 中也要为 \(tr[u]\) 所对应区间赋值。
\(build\) 是 \(O(nlogn)\) 的
接着,我们考虑单点修改。
假设当前我们要修改下标为 \(x\) 的数,那么从根节点开始,对于一个父节点, \(x\) 一定在它的左儿子或是右儿子。我们只要从中选择一个即可。
修改完儿子后,我们同样要 \(pushup\)。
void modify(int u, int x, int val) {if (tr[u].l == x && tr[u].r == x) {tr[u].v = val;} else {int mid = tr[u].l + tr[u].r >> 1;if (x <= mid) modify(u << 1, x, val);if (x > mid) modify(u << 1 | 1, x, val);pushup(u);}
}
\(modify\) 显然是 \(O(logn)\) 的。
然后是区间查询。
区间查询就是对于一个区间 \([l, r]\) 询问它的最大值,总和,或是其它线段树维护的值,这里以最大值为例。
对于线段树上的一个结点 \(u\),我们可以分四种情况:
- \(u\) 存储的区间被 \([l, r]\) 包含,那么我们直接范围 \(u\) 即可。
- \(u\) 属于 \([l, mid]\),那么我们递归左儿子。
- \(u\) 属于 \([mid + 1, r]\),我们递归右儿子。
- \(u\) 横跨左右儿子,我们左右一起递归。
下面是一个简便写法。
int query(int u, int l, int r) {if (l <= tr[u].l && tr[u].r <= r) return tr[u].v;int mid = tr[u].l + tr[u].r >> 1;int s = 0;if (l <= mid) s = query(u << 1, l, r);if (r > mid) s = max(s, query(u << 1 | 1, l, r));return s;
}
为什么要分四种情况讨论呢?因为有的题目需要我们维护一些横跨两个子区间的信息,所以需要在第四种情况时进行额外的操作。
由于答案一般能够分成 \(O(logn)\) 个区间,所以 \(query\) 的时间复杂度是 \(O(logn)\) 的。
然后是比较困难的区间修改。
我们首先可以想到对于区间的每个点进行单点修改,但这样过于慢。我们发现,如果对一段区间进行修改后,它的儿子的值也都会变化,所以在最坏情况下我们会遍历整棵树。
这里我们引入懒标记,即为了偷懒而生的标记。我们在维护线段树上结点的信息的同时,再维护一个 \(add\)(这里以区间增加为例),意思是我们需要给该结点的所有儿子都加上 \(add\)(儿子是一个序列,如果长为 \(k\),那就相当于序列中的每个数都加 \(add\),即总和加 \(k\times add\))。
我们在执行区间修改的时候,如果某个结点表示的区间被询问的区间包含,那么就修改它的懒标记,同时更改这个区间的和。
void pushdown(int u) {STree &left = tr[u << 1], &right = tr[u << 1 | 1], &root = tr[u];if (root.add) {// 给区间内的每个数加上 add,那么区间的总和就要加上区间长度 * addleft.add += root.add, left.s += (LL)(left.r - left.l + 1) * root.add;right.add += root.add, right.s += (LL)(right.r - right.l + 1) * root.add;root.add = 0;}
}
void modify(int u, int l, int r, int d) {if (l <= tr[u].l && tr[u].r <= r) {tr[u].add += d;tr[u].s += (LL)(tr[u].r - tr[u].l + 1) * d;} else {pushdown(u);int mid = tr[u].l + tr[u].r >> 1;if (l <= mid) modify(u << 1, l, r, d);if (r > mid) modify(u << 1 | 1, l, r, d);pushup(u);}
}
LL query(int u, int l, int r) {if (l <= tr[u].l && tr[u].r <= r) return tr[u].s;pushdown(u);int mid = tr[u].l + tr[u].r >> 1; LL res = 0;if (l <= mid) res += query(u << 1, l, r);if (r > mid) res += query(u << 1 | 1, l, r);return res;
}
我们发现在 \(modify\) 中多出了一个 \(pushdown\),它的含义就是将父亲的懒标记下传,因为此时我们要遍历子区间了。
同时查询操作也要加上 \(pushdown\) 操作。
245. 你能回答这些问题吗 - AcWing题库
我们考虑在线段树中维护 \(lmax\),意思是当前区间最大连续前缀和,同样维护 \(rmax\)。
此时父节点的最大连续子段和就是子节点的最大连续子段和,以及左儿子的 \(rmax\) 加上右儿子的 \(lmax\) 的最大值。
#include <bits/stdc++.h>
using namespace std;
const int N = 500010;
int n, m;
int a[N];struct Stree {int l, r, s, smax, lmax, rmax;
} tr[N * 4];void pushup(Stree &u, Stree &a, Stree &b) {u.s = a.s + b.s;u.lmax = max(a.lmax, a.s + b.lmax);u.rmax = max(b.rmax, a.rmax + b.s);u.smax = max({a.smax, b.smax, a.rmax + b.lmax});
}void pushup(int u) {pushup(tr[u], tr[u << 1], tr[u << 1 | 1]);
}void build(int u, int l, int r) {if (l == r) tr[u] = {l, r, a[r], a[r], a[r], a[r]};else {tr[u] = {l, r};int mid = l + r >> 1;build(u << 1, l, mid); build(u << 1 | 1, mid + 1, r);pushup(u);}
}void modify(int u, int x, int v) {if (tr[u].l == x && tr[u].r == x) tr[u].s = tr[u].smax = tr[u].lmax = tr[u].rmax = v;else {int mid = tr[u].l + tr[u].r >> 1;if (x <= mid) modify(u << 1, x, v);else modify(u << 1 | 1, x, v);pushup(u);}
}Stree query(int u, int l, int r) {if (tr[u].l >= l && tr[u].r <= r) return tr[u];else {int mid = tr[u].l + tr[u].r >> 1;if (r <= mid) return query(u << 1, l, r);else if (l > mid) return query(u << 1 | 1, l, r);else {auto a = query(u << 1, l, r), b = query(u << 1 | 1, l, r);Stree c;pushup(c, a, b);return c;}}
}int main() {scanf("%d%d", &n, &m);for (int i = 1; i <= n; i ++) scanf("%d", &a[i]);build(1, 1, n);while (m --) {int op, l, r;scanf("%d%d%d", &op, &l, &r);if (op == 1) {if (l > r) swap(l, r);printf("%d\n", query(1, l, r).smax);} else {modify(1, l, r);}}return 0;
}
246. 区间最大公约数 - AcWing题库
由更相减损术我们可以知道:
这其实是差分的形式,这启发我们用线段树维护差分。
具体我们可以在线段树中维护差分,具体地我们维护一个 \(s\) 表示 \([l, r]\) 的差分和,再维护一个 \(d\) 表示 \([l, r]\) 的最大公约数。
那么原来的式子就可以表示为 \(gcd(w[i], gcd(b[i + 1], ..., b[j])) = gcd(query(1, i).s, query(i + 1, j).d)\),其中 \(query\) 返回的是一整个线段树结点。
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 500010;
int n, m;
LL w[N];struct Stree {int l, r; LL s, d;
} tr[N * 4];LL gcd(LL a, LL b) {return b ? gcd(b, a % b) : abs(a);
}void pushup(Stree &u, Stree &l, Stree &r) {u.s = l.s + r.s;u.d = gcd(l.d, r.d);
}void pushup(int u) {pushup(tr[u], tr[u << 1], tr[u << 1 | 1]);
}void build(int u, int l, int r) {if (l == r) tr[u] = {l, r, w[r] - w[l - 1], w[r] - w[l - 1]};else {tr[u] = {l, r}; int mid = l + r >> 1;build(u << 1, l, mid); build(u << 1 | 1, mid + 1, r);pushup(u);}
}void modify(int u, int x, LL v) {if (tr[u].l == x && tr[u].r == x) tr[u] = {x, x, tr[u].s + v, tr[u].s + v};else {int mid = tr[u].l + tr[u].r >> 1;if (x <= mid) modify(u << 1, x, v);else modify(u << 1 | 1, x, v);pushup(u);}
}Stree query(int u, int l, int r) {if (tr[u].l >= l && tr[u].r <= r) return tr[u];else {int mid = tr[u].l + tr[u].r >> 1;if (l > mid) return query(u << 1 | 1, l, r);else if (r <= mid) return query(u << 1, l, r);else {auto a = query(u << 1, l, r), b = query(u << 1 | 1, l, r);Stree c;pushup(c, a, b);return c;}}
}int main() {scanf("%d%d", &n, &m);for (int i = 1; i <= n; i ++) scanf("%lld", &w[i]);build(1, 1, n);while (m --) {char op[2]; int l, r; LL d;scanf("%s%d%d", op, &l, &r);if (*op == 'Q') {if (l == r) printf("%lld\n", query(1, 1, l).s);else {auto a = query(1, 1, l), b = query(1, l + 1, r);printf("%lld\n", gcd(a.s, b.d));}} else {scanf("%lld", &d);modify(1, l, d); if (r + 1 <= n) modify(1, r + 1, -d);}}return 0;
}
243. 一个简单的整数问题2 - AcWing题库
懒标记模板。
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 100010;
int n, m, w[N];struct STree {int l, r;LL s, add;
} tr[N * 4];void pushup(int u) {tr[u].s = tr[u << 1].s + tr[u << 1 | 1].s;
}void pushdown(int u) {STree &left = tr[u << 1], &right = tr[u << 1 | 1], &root = tr[u];if (root.add) {left.add += root.add, left.s += (LL)(left.r - left.l + 1) * root.add;right.add += root.add, right.s += (LL)(right.r - right.l + 1) * root.add;root.add = 0;}
}void build(int u, int l, int r) {if (l == r) tr[u] = {l, r, w[r], 0};else {int mid = l + r >> 1;tr[u] = {l, r};build(u << 1, l, mid); build(u << 1 | 1, mid + 1, r);pushup(u);}
}void modify(int u, int l, int r, int d) {if (l <= tr[u].l && tr[u].r <= r) {tr[u].add += d;tr[u].s += (LL)(tr[u].r - tr[u].l + 1) * d;} else {pushdown(u);int mid = tr[u].l + tr[u].r >> 1;if (l <= mid) modify(u << 1, l, r, d);if (r > mid) modify(u << 1 | 1, l, r, d);pushup(u);}
}LL query(int u, int l, int r) {if (l <= tr[u].l && tr[u].r <= r) return tr[u].s;pushdown(u);int mid = tr[u].l + tr[u].r >> 1; LL res = 0;if (l <= mid) res += query(u << 1, l, r);if (r > mid) res += query(u << 1 | 1, l, r);return res;
}int main() {scanf("%d%d", &n, &m);for (int i = 1; i <= n; i ++) scanf("%d", &w[i]);build(1, 1, n);while (m --) {char op[2]; int l, r;scanf("%s%d%d", op, &l, &r);if (*op == 'C') {int d; scanf("%d", &d);modify(1, l, r, d);} else {printf("%lld\n", query(1, l, r));}}return 0;
}
扫描线
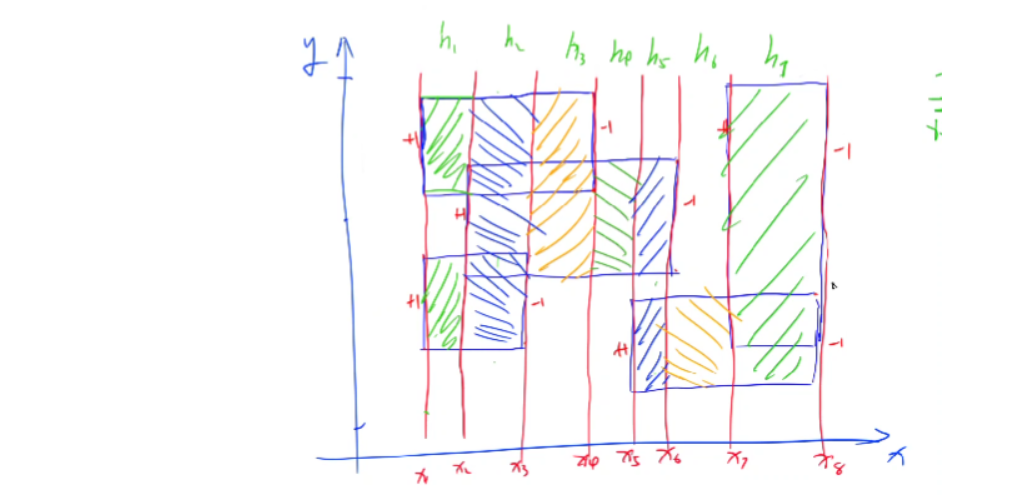
假设当前平面内有一堆的矩形,我们要统计它们的面积(不能重复),那么我们就可以像下图一样,用一条平行 \(y\) 轴的扫描线从左往右,扫。根据下图,总面积就应该是 \(\sum^{2n - 1}_{i = 1}h_i \times (x_{i + 1} - x_i)\),其中 \(n\) 为矩形的数量,\(h_i\) 为扫描线上覆盖有矩形的长度。
具体地,我们把每扫到一个矩形的左宽,就把左宽覆盖的区间 \(+1\),扫到右宽就 \(-1\),这样就可以算出 \(h_i\)。
我们发现该操作设计区间修改和区间查询,所以我们考虑用线段树加速。
线段树中存储 \(cnt\) 表示直接完全覆盖此区间的矩形数量,\(len\) 表示此区间被矩形覆盖的长度。
并且注意,线段树上的每个叶节点存的都是区间,所以需要注意坐标。
根据以上的存储方式,可能会出现子节点的 \(cnt\) 大于父节点的 \(cnt\) 的情况。
我们再考虑 \(pushup\) 操作如何写。分三种情况:
- \(cnt \ne 0\),说明该区间被完全覆盖,\(len\) 就为该区间的长度。
- \(cnt = 0\),且 \(l \ne r\),可以用左儿子和右儿子来更新自己。
- \(cnt = 0\),且 \(l = r\),不合法,无用线段,\(len = 0\)
我们可以通过一些手段证明 \(pushdown\) 某些时候是不用写的。(另外一些时候比如第二道例题要写,下文会提到)。
引用的证明:
此时 \(cnt\) 表达的含义:当前区间被覆盖的次数,跟其它节点无关。
可以发现,因为对于修改区间 \([l, r]\) 操作,是一对一对的。
所以,一个节点代表的区间被覆盖的次数不需要继承其父亲信息的情况。
因此需要去掉 \(pushDown\)。
我们 \(Atlantis\) 一题为例。
247. 亚特兰蒂斯 - AcWing题库
在上文的思路上,由于本题坐标可能有小数,所以需要进行离散化。
#include <bits/stdc++.h>
using namespace std;
const int N = 10010;
int n;
vector<double> tmp;struct Segment {double x, y1, y2;int k;bool operator < (const Segment &t) const{return x < t.x;}
} segs[N * 2];struct Stree {int l, r, cnt;double len;
} tr[N * 8];// tmp 存的是小数,它在 tmp 中的位置就是离散化的值
// find 查找的是某个小数被映射到了什么位置
int find(double v) {return lower_bound(tmp.begin(), tmp.end(), v) - tmp.begin();
}void pushup(int u) {if (tr[u].cnt) {tr[u].len = tmp[tr[u].r + 1] - tmp[tr[u].l];} else if (tr[u].l != tr[u].r) {tr[u].len = tr[u << 1].len + tr[u << 1 | 1].len;} else {tr[u].len = 0;}
}void build(int u, int l, int r) {if (l == r) tr[u] = {l, r, 0, 0};else {tr[u] = {l, r};int mid = l + r >> 1;build(u << 1, l, mid); build(u << 1 | 1, mid + 1, r);}
}void modify(int u, int l, int r, int d) {if (l <= tr[u].l && tr[u].r <= r) {tr[u].cnt += d; pushup(u);} else {int mid = tr[u].l + tr[u].r >> 1;if (l <= mid) modify(u << 1, l, r, d);if (r > mid) modify(u << 1 | 1, l, r, d);pushup(u);}
}int main() {int T = 0;while (scanf("%d", &n), n) {tmp.clear();for (int i = 1, j = 0; i <= n; i ++) {double x_1, y_1, x_2, y_2;scanf("%lf%lf%lf%lf", &x_1, &y_1, &x_2, &y_2);segs[j ++] = {x_1, y_1, y_2, 1};segs[j ++] = {x_2, y_1, y_2, -1};tmp.push_back(y_1); tmp.push_back(y_2);}sort(segs, segs + 2 * n);sort(tmp.begin(), tmp.end());tmp.erase(unique(tmp.begin(), tmp.end()), tmp.end());build(1, 0, tmp.size() - 2); double res = 0;for (int i = 0; i < n * 2; i ++) {if (i > 0) res += tr[1].len * (segs[i].x - segs[i - 1].x);modify(1, find(segs[i].y1), find(segs[i].y2) - 1, segs[i].k);}printf("Test case #%d\n", ++ T);printf("Total explored area: %.2lf\n\n", res);}return 0;
}
248. 窗内的星星 - AcWing题库
题解 P1502 【窗口的星星】 - 洛谷专栏 (luogu.com.cn)
思路这篇题解说的很明白,我们来谈谈这个问题为什么需要懒标记。
最重要的一点是,我们线段树中存的数据不再是 \(cnt\) 和 \(len\),而是 \(sm\) 表示的该子区间对应的亮度总和。亮度的增加不同于 \(cnt\) 是要下传的。并且线段树中叶子存的区间不再是 \([l, l+1]\) 而是 \([l, l]\),可以理解为一个点。所以我们需要 \(lasytag\) 来帮助操作。
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 10010;
int n, w, h;
vector<LL> tmp;struct Segment {LL x, l, r, c;bool operator < (const Segment &t) const{return x < t.x || x == t.x && c > t.c;}
} segs[N * 2];struct Stree {int l, r; LL sm, add;
} tr[N * 8];LL find(LL x) {return lower_bound(tmp.begin(), tmp.end(), x) - tmp.begin();
}void pushup(int u) {tr[u].sm = max(tr[u << 1].sm, tr[u << 1 | 1].sm);
}void pushdown(int u) {if (tr[u].add) {tr[u << 1].sm += tr[u].add;tr[u << 1].add += tr[u].add;tr[u << 1 | 1].sm += tr[u].add;tr[u << 1 | 1].add += tr[u].add;tr[u].add = 0; }
}void build(int u, int l, int r) {tr[u] = {l, r, 0, 0};if (l != r) {int mid = l + r >> 1;build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);}
}void modify(int u, int l, int r, int d) {if (l <= tr[u].l && tr[u].r <= r) {tr[u].sm += d, tr[u].add += d;} else {int mid = tr[u].l + tr[u].r >> 1;pushdown(u);if (l <= mid) modify(u << 1, l, r, d);if (r > mid) modify(u << 1 | 1, l, r, d);pushup(u);}
}int main() {ios::sync_with_stdio(false);cin.tie(0); cout.tie(0);while (cin >> n >> w >> h) {tmp.clear();for (int i = 1, j = 0; i <= n; i ++) {LL x, y, c;cin >> x >> y >> c;segs[j ++] = {x, y, y + h - 1, c};segs[j ++] = {x + w - 1, y, y + h - 1, -c};tmp.push_back(y); tmp.push_back(y + h - 1);}sort(tmp.begin(), tmp.end());tmp.erase(unique(tmp.begin(), tmp.end()), tmp.end());sort(segs, segs + n * 2); build(1, 0, tmp.size() - 1);LL res = 0;for (int i = 0; i < n * 2; i ++) {modify(1, find(segs[i].l), find(segs[i].r), segs[i].c);res = max(res, tr[1].sm);}cout << res << endl;}return 0;
}
动态开点
根据上文所说,一棵普通线段树要用到 \(4 n\) 的空间,我们为了节省空间,可以采用动态开点的方式。具体地,线段树上的每个结点的 \(l\) 和 \(r\) 不再表示它的左、右儿子,而是直接表示它的左、右子结点的坐标。所以在动态开点线段树中我们不能再用 \(p << 1\) 和 \(p << 1 | 1\) 来访问左右儿子,而是直接使用 \(tr[u].l\) 和 \(tr[u].r\)。为了简化代码,我们可以在程序开头宏定义 #define lc(u) tr[(u)].l(\(rc(u)\) 同理)。
总而言之,动态开点线段树的精髓就是只开要用到的点。动态开点线段树的空间复杂度应该是 \(mlogn\) 级别的,且一定小于 \(2n\)。
这里以 1275. 最大数 - AcWing题库 为例(即线段树维护区间最大值),代码如下。
#include <bits/stdc++.h>
using namespace std;
#define lc(x) tr[(x)].lc
#define rc(x) tr[(x)].rc
#define v(x) tr[(x)].v
const int N = 200010;int m, p, idx;
struct node {int lc, rc, v;
} tr[N << 1];void pushup(int u) {v(u) = max(v(lc(u)), v(rc(u)));
}void update(int &u, int l, int r, int x, int val) {if (!u) u = ++ idx;if (l == r) { v(u) = val; return; }int mid = l + r >> 1;if (x <= mid) update(lc(u), l, mid, x, val);else update(rc(u), mid + 1, r, x, val);pushup(u);
}int query(int u, int cl, int cr, int l, int r) {if (!u) return 0;if (l <= cl && cr <= r) return v(u);int mid = cl + cr >> 1;if (l > mid) return query(rc(u), mid + 1, cr, l, r);else if (r <= mid) return query(lc(u), cl, mid, l, r);else return max(query(lc(u), cl, mid, l, r), query(rc(u), mid + 1, cr, l, r));
}int main() {scanf("%d%d", &m, &p);int last = 0, n = 0, rt = 0;while (m --) {char s[2]; int x;scanf("%s%d", s, &x);if (*s == 'A') {x = ((long long)x + last) % p;update(rt, 1, 200000, ++ n, x);} else {last = query(rt, 1, 200000, n - x + 1, n);printf("%d\n", last);}}return 0;
}
这里的代码作为示例就不把线段树装进结构体里了,一般我的写法是:
struct segment_tree_node {int l, r;int ...
} tr[范围];
struct segment_tree {... // 需要使用的函数
} stree;stree.函数名;
动态开点其实有点类似于 Trie,在后面的部分会经常用到。
可持久化线段树(主席树)
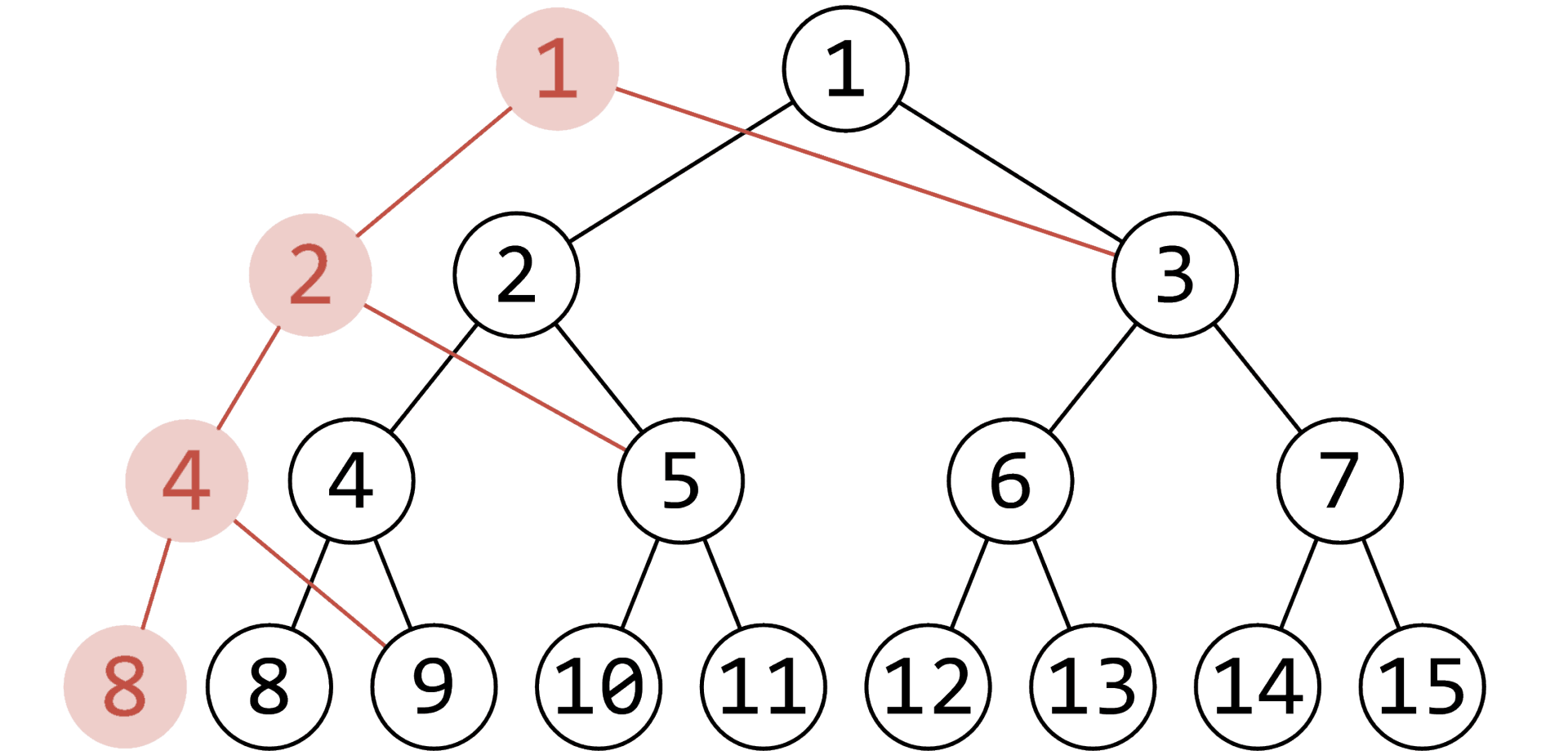
可持久化线段树(下文均称为主席树)指的是将线段树每一时刻的线段树都保存下来,进行查询的数据结构。可以与可持久化 Trie 进行类比。同样地,我们不能将所有版本都存下来。但是我们发现一次操作,比如单点修改,只会经过一条链上的点,所以我们可以从上一个版本开始遍历,将经过的所有点拷贝一份出来,进行修改。
如下图(来自 oiwiki),黑色的 \(1,2,4,8\) 属于上一个版本,我们以 \(2\) 举例。首先我们将 \(2\) 这个点拷贝一份给最新版本,然后考虑接下来要递归左子树还是右子树。对于假如我们递归左子树就更改最新版本新拷贝出来点的左儿子即可。
在刚刚的过程中我们其实可以发现所做的过程是不好用堆式存储的,所以我们选择动态开点。
我们直接来看一道经典例题。
P3834 【模板】可持久化线段树 2
本题需要求的是 \([l, r]\) 区间内的第 \(k\) 小数。我们可以使用权值主席树,根据上文的描述,我们可以很轻松地求出 \([1, r]\) 区间内的信息和 \([1, l - 1]\) 的信息,因为可以直接调用 \(r\) 和 \(l - 1\) 号版本。所以我们可以运用前缀和的思想,同时遍历两个版本,然后错位相减即可求出答案。
具体过程中,如果左子树的结点个数 \(cnt\) 大于等于当前要求的 \(k\),我们就递归左子树,否则我们递归右子树并让 \(k - cnt\)。
由于值域很大,我们需要离散化。接着再分析一下空间问题,由于我们是动态开点,且维护的是值域线段树,所以总的空间应该是 \(O(MlogV + 2N - 1)\),这里 \(N,M\) 同阶,且离散化后 \(V\) 也和 \(N\) 同阶,所以可以看做 \(O(NlogN + 2N)\)。由于 \(N \leq 200000\),所以总共就 \(20N\) 左右,我们直接开到 \(N<<5\) 即可。
#include <bits/stdc++.h>
using namespace std;
#define lc(x) tr[(x)].l
#define rc(x) tr[(x)].r
#define v(x) tr[(x)].v
const int N = 200010;
int n, m, a[N], tmp[N];int cnt;
struct stree_node {int l, r, v;
} tr[N << 5];
struct Stree {void pushup(int u) {v(u) = v(lc(u)) + v(rc(u)); }// 这个 build 事实上毫无用处,因为并没有对值进行任何修改int build(int l, int r) {int p = ++ cnt;if (l == r) return p;int mid = l + r >> 1;lc(p) = build(l, mid); rc(p) = build(mid + 1, r);return p;}int modify(int q, int l, int r, int x, int val) {int p = ++ cnt;tr[p] = tr[q];if (l == r) { v(p) += val; return p; }int mid = l + r >> 1;if (x <= mid) lc(p) = modify(lc(q), l, mid, x, val);else rc(p) = modify(rc(q), mid + 1, r, x, val);pushup(p);return p;}int query(int q, int p, int l, int r, int k) {// 找到了if (l == r) return r;int cnt = v(lc(p)) - v(lc(q));int mid = l + r >> 1;if (k <= cnt) return query(lc(q), lc(p), l, mid, k);else return query(rc(q), rc(p), mid + 1, r, k - cnt);}
} stree;
int rt[N];int main() {scanf("%d%d", &n, &m);for (int i = 1; i <= n; i ++) { scanf("%d", &a[i]); tmp[i] = a[i]; }sort(tmp + 1, tmp + 1 + n);int k = unique(tmp + 1, tmp + 1 + n) - tmp - 1;for (int i = 1; i <= n; i ++) a[i] = lower_bound(tmp + 1, tmp + 1 + k, a[i]) - tmp;rt[0] = stree.build(1, k); // 同理这一句也没用for (int i = 1; i <= n; i ++) rt[i] = stree.modify(rt[i - 1], 1, k, a[i], 1); while (m --) {int l, r, x; scanf("%d%d%d", &l, &r, &x);printf("%d\n", tmp[stree.query(rt[l - 1], rt[r], 1, k, x)]);}return 0;
}
先写这些,其它的题有空再写。
线段树合并
线段树合并会用到动态开点,所以上文特地提了几句。
顾名思义,线段树合并就是把两棵线段树合并在一起。我们同样地动态开点,假设要将 \(B\) 合并到 \(A\),那么就从 \(A\) 和 \(B\) 两棵线段树的根出发,往儿子递归。如果在某一时刻 \(A\) 或 \(B\) 对应的结点是空的,就直接返回另一棵树上的对应节点。如果当前遍历到叶子结点,就将 \(B\) 对应的值加到 \(A\) 上。然后递归地合并左子树和右子树,做完了后再 \(pushup\) 一遍。
我们还是以一道题为例。
P4556 Vani有约会
题意概括一下就是有两种操作,一种是给 \(x\) 到 \(y\) 的路径上的每个点发一包 \(z\) 类型的储备粮,一种是查询一个点上储存最多的是哪种类型的粮。
我们会发现在树上区间修改的话是非常不好做的,所以我们考虑将操作一转换为差分。就应该是在 \(y\) 到根节点的路径上发一包 \(z\),\(x\) 到根节点的路径上发一包 \(z\),在 \(lca(x, y)\) 到根节点的路径上处没收一包 \(z\),因为 \(lca\) 是被重复计算了,最后再在 \(fa_{lca(x, y)}\) 到根节点的路径上没收一包 \(z\)。我们发现这其实可以直接单点修改,最后再从下往上做一次前缀和即可。
于是我们可以想到,对于每一个结点动态开一棵权值线段树,每次进行四次单点修改。最后再从下往上进行线段树合并即可。
我们分析一下空间,由于每个修改会转换为四次操作,所以总共的空间应该是 \(O(4MlogV + 2N)\),转化为 \(4NlogN + 2N\),其中 \(logN\) 大概是 \(17\),我们直接开 \(80N\) 即可。
再看时间,我们分析线段树合并的过程,显然每次执行 \(merge\) 递归时,一定会将一个点合并到另一个点上,相当于每个点只递归一次(注意是相当),这样总共的复杂度就应该和线段树的总点数同阶。大概是 \(mlogn\) 级别的。当然这个复杂度并不是非常科学,而且常数比较大。还是更建议使用可并堆,可并堆后面会另开分享。
代码:
#include <bits/stdc++.h>
using namespace std;
#define lc(x) tr[(x)].l
#define rc(x) tr[(x)].r
const int N = 100010;int h[N], e[N << 1], ne[N << 1], idx;
void add(int a, int b) {e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}int n, m, cnt; struct Stree_node {int l, r, s, p;
} tr[N * 20 * 4];
struct Stree {void pushup(int u) {int l = lc(u), r = rc(u);if (!l || tr[l].s < tr[r].s) tr[u].s = tr[r].s, tr[u].p = tr[r].p;else tr[u].s = tr[l].s, tr[u].p = tr[l].p;}void modify(int &u, int l, int r, int x, int val) {if (!u) u = ++ cnt;if (l == r) { tr[u].s += val, tr[u].p = x; return; }int mid = l + r >> 1;if (x <= mid) modify(lc(u), l, mid, x, val);else modify(rc(u), mid + 1, r, x, val);pushup(u);}int merge(int a, int b, int l, int r) {if (!a || !b) return a + b;if (l == r) { tr[a].s += tr[b].s; return a; }int mid = l + r >> 1;lc(a) = merge(lc(a), lc(b), l, mid);rc(a) = merge(rc(a), rc(b), mid + 1, r);pushup(a);return a;}
} stree; int fa[N][20], depth[N];
void init() {queue<int> q; q.push(1);memset(depth, 0x3f, sizeof depth);depth[0] = 0, depth[1] = 1;while (q.size()) {int ver = q.front(); q.pop();for (int i = h[ver]; ~i; i = ne[i]) {int j = e[i];if (depth[j] > depth[ver] + 1) {depth[j] = depth[ver] + 1;q.push(j);fa[j][0] = ver;for (int k = 1; k < 20; k ++)fa[j][k] = fa[fa[j][k - 1]][k - 1]; }}}
}
int lca(int a, int b) {if (depth[a] < depth[b]) swap(a, b);for (int i = 19; i >= 0; i --)if (depth[fa[a][i]] >= depth[b])a = fa[a][i];if (a == b) return a;for (int i = 19; i >= 0; i --)if (fa[a][i] != fa[b][i])a = fa[a][i], b = fa[b][i];return fa[a][0];
}// rt 指的是每棵线段树的根节点位置
int rt[N], ans[N];
void calc(int u, int father) {for (int i = h[u]; ~i; i = ne[i]) {int j = e[i];if (j == father) continue;calc(j, u);rt[u] = stree.merge(rt[u], rt[j], 1, 100000);} ans[u] = tr[rt[u]].p;// 这里要根据题意特判if (tr[rt[u]].s == 0) ans[u] = 0;
} int main() {scanf("%d%d", &n, &m);memset(h, -1, sizeof h);for (int i = 1; i < n; i ++) {int a, b; scanf("%d%d", &a, &b);add(a, b); add(b, a);}init();while (m --) {int x, y, z; scanf("%d%d%d", &x, &y, &z);stree.modify(rt[x], 1, 100000, z, 1);stree.modify(rt[y], 1, 100000, z, 1);int LCA = lca(x, y);stree.modify(rt[LCA], 1, 100000, z, -1);stree.modify(rt[fa[LCA][0]], 1, 100000, z, -1);}calc(1, -1);for (int i = 1; i <= n; i ++) printf("%d\n", ans[i]);return 0;
}
这种数据结构题其实并不是很难写,因为基本上全都是模板,具体操作的时候添加一下就行了。
最后一个事实是,带 \(lazy\) 的线段树合并很困难,听说可以用标记永久化,但感觉比较黑科技。
P8123 BalticOI 2021 Day1 Inside information(主席树合并)
这道题需要一些小技巧。
首先我们发现 \(S\) 和 \(Q\) 操作就是裸的线段树合并,和上题的思路类似,每个结点开一棵权值线段树即可,查询就正常线段树查询。
那么 \(C\) 操作怎么做呢?我们显然不能把所有的树全部都跑一遍。但我们可以将每个合并操作视为连边,以合并的时间为边权画出图。
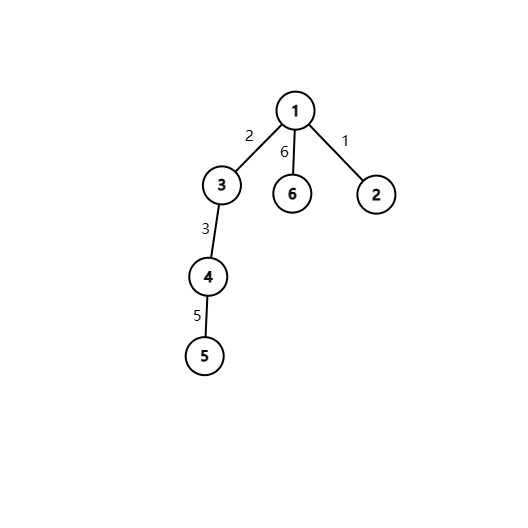
如上图。我们首先要搞清楚如果 \(A\) 先和 \(B\) 合并,再和 \(C\) 合并,此时的 \(A\) 和 \(B\) 是不一样的,但是 \(B\) 一定被 \(A\) 包含。我们发现一个点 \(u\) 能包含 \(v\) 的条件是 \(u\) 到 \(v\) 的边权单调递减,原因就是刚才提到的。现在我们要求的是有多少个点含有一个数据块 \(a\),就相当于求符合 \(a\) 到 \(b\) 的路径上边权单调递增的点的数量加一(因为还有自己)。注意如果一个路径上只有一条边那它也是答案。
单调递增不是很好用线段树合并时维护(即 $$),于是我们可以想到倒序建图,即从最后一个合并操作开始,第一个合并操作结束。还是样例,我们可以建出这么一个图:
我们会发现此时的答案就时所有单调递减能到的边了,这是很好用线段树合并维护的。而且由于我们是先把所有的操作都进行完,再进行查询操作,相当于离线,所以需要主席树。
主席树合并和普通树合并很像,直接在下文代码中体现了。
#include <bits/stdc++.h>
using namespace std;
const int N = 240010;
int n, k;struct stree_node {int l, r; int v;
} tr[N << 5];
int cnt;
struct Stree {void pushup(int u) {tr[u].v = tr[tr[u].l].v + tr[tr[u].r].v;}int modify(int q, int l, int r, int x, int val) {int p = ++ cnt;tr[p] = tr[q]; // 警钟长鸣,这是一颗可持久化线段树,这一行一定不能漏if (l == r) { tr[p].v += val; return p; }int mid = l + r >> 1;if (x <= mid) tr[p].l = modify(tr[q].l, l, mid, x, val);else tr[p].r = modify(tr[q].r, mid + 1, r, x, val);pushup(p);return p;}int merge(int a, int b, int l, int r) {if (!a || !b) return a + b;int u = ++ cnt;if (l == r) { tr[u].v = tr[a].v + tr[b].v; return u; }int mid = l + r >> 1;tr[u].l = merge(tr[a].l, tr[b].l, l, mid);tr[u].r = merge(tr[a].r, tr[b].r, mid + 1, r);pushup(u);return u;}int query1(int u, int l, int r, int x) {if (l == r) return tr[u].v;int mid = l + r >> 1;if (x <= mid) return query1(tr[u].l, l, mid, x);else return query1(tr[u].r, mid + 1, r, x);}int query2(int u, int l, int r, int x) {if (!u || l > x || r < 1) return 0;if (r <= x) return tr[u].v;int mid = l + r >> 1;return query2(tr[u].r, mid + 1, r, x) + query2(tr[u].l, l, mid, x); }
} stree;struct node {int a, d, op;
} q[N];
int ans[N], rt[N];int main() {scanf("%d%d", &n, &k);for (int i = 1; i <= n; i ++) rt[i] = stree.modify(0, 1, n, i, 1);for (int i = 1; i < n + k; i ++) {char op[2]; scanf("%s", op);if (*op == 'S') {int a, b; scanf("%d%d", &a, &b); q[i] = {a, b, 0};rt[a] = rt[b] = stree.merge(rt[a], rt[b], 1, n);} else if (*op == 'Q') {int a, d; scanf("%d%d", &a, &d);q[i] = {a, d, 1};ans[i] = stree.query1(rt[a], 1, n, d);} else {int x; scanf("%d", &x);q[i] = {x, 0, 2};}}memset(tr, 0, sizeof tr); cnt = 0;for (int i = 1; i <= n; i ++) rt[i] = ++ cnt;// 维护时刻 t 有多少加入for (int i = n + k - 1; i; i --)if (!q[i].op) {int a = q[i].a, b = q[i].d;rt[a] = stree.modify(rt[a], 1, n + k - 1, i, 1);rt[a] = stree.merge(rt[a], rt[b], 1, n + k - 1); rt[b] = rt[a];}for (int i = 1; i < n + k; i ++)if (q[i].op == 1) puts(ans[i] ? "yes" : "no");else if (q[i].op == 2) printf("%d\n", stree.query2(rt[q[i].a], 1, n + k - 1, i) + 1);return 0;
}