LGV 引理
概述
参考 OI Wiki
Lindström–Gessel–Viennot lemma,即 LGV 引理,可以用来处理有向无环图上不相交路径计数等问题。
引理

定义方阵 \(M\)。
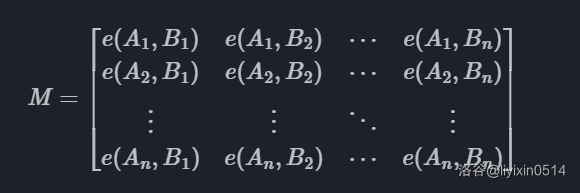
结论是:
\[\det(M) = \sum_{S:A\to B} (-1)^{sgn(\sigma(S))} \prod_{i=1}^n \omega(S_i)
\]
其中 \(S:A\to B\) 表示不相交路径集合。
证明?我不会。鸽掉,不一定补。
参考 OI Wiki
Lindström–Gessel–Viennot lemma,即 LGV 引理,可以用来处理有向无环图上不相交路径计数等问题。

定义方阵 \(M\)。
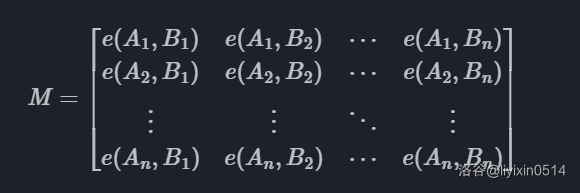
结论是:
其中 \(S:A\to B\) 表示不相交路径集合。
证明?我不会。鸽掉,不一定补。
本文来自博客园,作者:liyixin,转载请注明原文链接:https://www.cnblogs.com/liyixin0514/p/18648738
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.hqwc.cn/news/863078.html
如若内容造成侵权/违法违规/事实不符,请联系编程知识网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!