哈迪-温伯格平衡及拓展

目录

• • 五个条件：
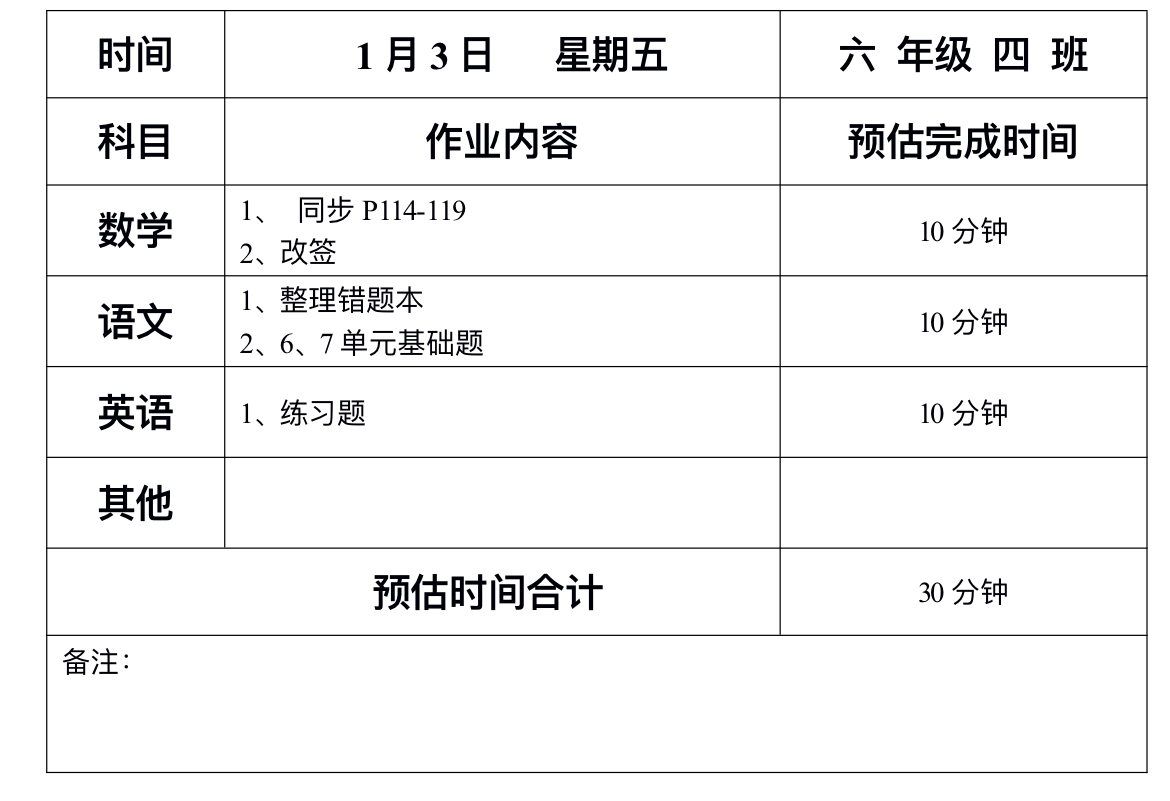
• 特殊情况
  • 基因频率父本≠母本
  • 伴X遗传
    • • • 法一
        • 法二
• 拓展
  • 1. 有突变
  • 2. 有选择
    • 2.1. 定向选择
      • 2.1.1 对\(aa\)不利
        • 极端情况：\(s=1\)
        • 加上突变
      • 2.1.2 对\(A\_\)不利
    • 2.2 分裂选择
    • 2.3 稳定选择
  • 3. 有迁移
    • • • 法一
        • 法二

设 \(P(A)=p,P(a)=q\)
自由交配一代后：

\(AA\)	\(Aa\)	\(aa\)
\(p^2\)	\(2pq\)	\(q^2\)

五个条件：

1. 无限大群体
2. 无突变
3. 无选择
4. 无迁移
5. 无选型交配

其实还有几个条件：

1. 父本中基因频率与母本相同
2. 非复等位基因
3. 非伴性遗传

特殊情况

基因频率父本≠母本

	\(p_♂\)	\(q_♂\)
\(p_♀\)	\(p_♂p_♀\)	\(q_♂p_♀\)
\(q_♀\)	\(p_♂q_♀\)	\(q_♂q_♀\)

自由交配一代后

\[p_{F1}=p_♂p_♀+\frac{1}{2}(q_♂p_♀+p_♂q_♀)\\ \begin{aligned} \because p_♂+q_♂&=1\\ p_♂+q_♂&=1\\ \end{aligned}\\ \begin{aligned} \therefore p_{F1}&=\cfrac{p_♂+p_♀}{2}\\ \textsf{同理 }q_{F1}&=\cfrac{q_♂+q_♀}{2}\\ \end{aligned} \]

\[\tag{*} \]

即下一代的基因频率是上一代的平均值

再自由交配一代后 \(F2\) 遵循哈温平衡

\(AA\)	\(Aa\)	\(aa\)
\(\cfrac{(p_♂+p_♀)^2}{4}\)	\(\cfrac{(p_♂+p_♀)(q_♂+q_♀)}{2}\)	\(\cfrac{(q_♂+q_♀)^2}{4}\)

伴X遗传

由结论 \((\text{*})\)，下一代♀基因频率是上一代的平均值
由交叉遗传，下一代♂基因频率是上一代的♀

设 \(x\) 世代 \(p_♂=M_x\)，\(p_♀=N_x\)
所以：

\[\begin{cases} M_x&=N_{x-1}\\ N_x&=\cfrac{M_{x-1}+N_{x-1}}{2} \end{cases}\\ \therefore N_x=\cfrac{N_{x-1}+N_{x-2}}{2} \]

通项公式：

\[N_x = \cfrac{2p_♀ + p_♂}{3} + \left(-\frac{1}{2}\right)^x \cfrac{p_♀ - p_♂}{3} \]

所以，\(x\to\infty\) 时，\(N_x=\cfrac{2p_♀ + p_♂}{3}\)

法一

Inspired by Microsoft Copilot

设通项公式 \(N_x=r^x\)
代入得：

\[\begin{aligned} r^x&=\cfrac{r^{x-1}+r^{x-2}}{2}\\ 2r^x&=r^{x-1}+r^{x-2}\\ 2r^x-r-1&=0\\ r&=1\text{ or }-\frac{1}{2} \end{aligned} \]

因此，通项公式可以表示为：

\[\begin{aligned} N_x &= A \cdot 1^x + B \cdot \left(-\frac{1}{2}\right)^x\\ &= A + B \left(-\frac{1}{2}\right)^x \end{aligned} \]

其中，$ A $ 和 $ B $ 是由 \(N_0\) 与 \(N_1\) 决定的常数
代入初始条件 $ N_0 = p_♀ $ 和 $ N_1 = \cfrac{p_♀ + p_♂}{2} $：

\[\begin{cases} A &= \cfrac{2p_♀ + p_♂}{3}\\ B &= \cfrac{p_♀ - p_♂}{3} \end{cases} \]

因此，通项公式为：

\[N_x = \cfrac{2p_♀ + p_♂}{3} + \left(-\frac{1}{2}\right)^x \cfrac{p_♀ - p_♂}{3} \]

法二

设 \(p_♀-p_♂=a\)

小奥启动！

\[\def\simi{(-\cfrac{1}{2})} \begin{aligned} S&=\sum_{i=0}^{x}{\simi^i}\\ \simi S&=\sum_{i=1}^{x+1}{\simi^i}\\ S-\simi S&=1-\simi^{x+1}\\ S&=\frac{2}{3}+\frac{1}{3}\simi^x\\ N_x&=aS+p_♂\\ &=\cfrac{2p_♀ + p_♂}{3} + \left(-\frac{1}{2}\right)^x \cfrac{p_♀ - p_♂}{3} \end{aligned} \]

拓展

1. 有突变

\[A\xrightleftharpoons[v]{u}a \]

平衡时有：

\[\begin{cases} pu=qv\\ p+q=1 \end{cases} \]

解得：

\[\begin{cases} p=\cfrac{v}{u+v}\\ q=\cfrac{u}{u+v} \end{cases} \]

2. 有选择

基因型频率	\(AA\)	\(Aa\)	\(aa\)	合计
初始	\(p^2\)	\(2pq\)	\(q^2\)	\(1\)
适合度	\(m\)	\(n\)	\(o\)
选择后	\(mp^2\)	\(2npq\)	\(oq^2\)	\(T=mp^2+2npq+oq^2\)
相对频率	\(\cfrac{mp^2}{T}\)	\(\cfrac{2npq}{T}\)	\(\cfrac{oq^2}{T}\)	\(1\)

下一轮 \(P(A)\)频率

\[\begin{aligned} p'&=P'(AA)+\cfrac{P'(Aa)}{2}\\ &=p\cfrac{mp+nq}{T} \end{aligned} \]

\(P(A)\) 改变量

\[\begin{aligned} \Delta p&=p'-p\\ &=p(\cfrac{mp+nq}{T}-1)\\ &=p\cfrac{mp(1-p)+nq(1-2p)-oq^2}{T}\\ \because &\ 1-p=q,\ 1-2p=q-p\\ \Delta p&=p\cfrac{mpq+nq(q-p)-oq^2}{T}\\ &=pq\cfrac{p(m-n)+q(n-o)}{T} \end{aligned} \]

综上，当选择平衡时，\(\Delta p=0\)，

\[\tag{1}p(m-n)=q(o-n) \]

美丽而简洁。

而选择的公式推出来了：

\[\tag{2}\Delta p=pq\cfrac{p(m-n)+q(n-o)}{T} \]

2.1. 定向选择

2.1.1 对\(aa\)不利

基因型频率	\(AA\)	\(Aa\)	\(aa\)	合计
初始	\(p^2\)	\(2pq\)	\(q^2\)	\(1\)
选择系数	\(0\)	\(0\)	\(s\)
适合度	\(1\)	\(1\)	\(o=1-s\)
选择后	\(p^2\)	\(2pq\)	\((1-s)q^2\)	\(T=1-sq^2\)
相对频率	\(\cfrac{p^2}{T}\)	\(\cfrac{2pq}{T}\)	\(\cfrac{(1-s)q^2}{T}\)	\(1\)

带入式 \((2)\) 得：

\[\begin{aligned} -\Delta q=\Delta p&=pq\cfrac{p(1-1)+q(1-o)}{T}\\ &=\cfrac{spq^2}{1-sq^2} \\ q'&=q+\Delta q\\ &=q\cfrac{1-sq}{1-sq^2} \end{aligned} \]

显然，\(q'>0\)。

所以选择不能淘汰 \(a\) 基因。

极端情况：\(s=1\)

\[\begin{aligned} q_1&=q_0\cfrac{1-q_0}{1-q_0^2} =\cfrac{q_0}{q_0+1}\\ q_2&=\cfrac{q_1}{q_1+1} =\cfrac{\cfrac{q_0}{q_0+1}}{1+\cfrac{q_0}{q_0+1}} =\cfrac{q_0}{2q_0+1}\\ \vdots\\ q_n&=\cfrac{q_0}{nq_0+1}\\ n&=\cfrac{1}{q_n}-\cfrac{1}{q_0} \end{aligned} \]

即要通过选择将基因 \(a\) 频率从 \(q_0\) 降至 \(q_n\) 需经过 \(n=\cfrac{1}{q_n}-\cfrac{1}{q_0}\) 个世代。

如 \(q_0=0.001\) , \(q_n=0.0001\) 则与经过 \(n=9000\) 个世代！

加上突变

\[A\xrightleftharpoons[v]{u}a \]

\[\begin{aligned} \Delta_{select}q&=\cfrac{-spq^2}{1-sq^2} \approx-spq^2\\ \Delta_{mutate}q&=pu\\ \Delta p&=\Delta_{select}q+\Delta_{mutate}q\\ &=pu-spq^2 \end{aligned} \]

选择平衡时：

\[q=\sqrt{\frac{u}{s}} \]

2.1.2 对\(A\_\)不利

\[\begin{aligned} \Delta T&=sp^2+2spq=sp(2-p)\\ p'&=\cfrac{p-sp^2-spq}{1-\Delta T}\\ &=p\frac{1-s}{1-\Delta T}\\ \Delta p&=p'-p\\ &=\cfrac{-spq^2}{1-sp(2-p)} \end{aligned} \]

2.2 分裂选择

对\(Aa\)不利，杂种劣势。

基因型频率	\(AA\)	\(Aa\)	\(aa\)	合计
初始	\(p^2\)	\(2pq\)	\(q^2\)	\(1\)
选择系数	\(0\)	\(s\)	\(0\)
适合度	\(1\)	\(n=1-s\)	\(1\)
选择后	\(p^2\)	\(2(1-s)pq\)	\(q^2\)	\(T=1-2spq\)
相对频率	\(\cfrac{p^2}{T}\)	\(\cfrac{2(1-s)pq}{T}\)	\(\cfrac{q^2}{T}\)	\(1\)

带入式 \((2)\)：

\[\Delta p=spq\cfrac{p-q}{1-2spq} \]

赢家通吃。

\[\Delta p \begin{cases} >0 & p>q & \textsf{最终只剩}p\\ =0 & p=q & \textsf{不稳定平衡点}\\ <0 & p<q & \textsf{最终只剩}q\\ \end{cases} \]

2.3 稳定选择

对\(AA\)、\(aa\)不利，杂种优势。

基因型频率	\(AA\)	\(Aa\)	\(aa\)	合计
初始	\(p^2\)	\(2pq\)	\(q^2\)	\(1\)
选择系数	\(s\)	\(0\)	\(t\)
适合度	\(m=1-s\)	\(1\)	\(o=1-t\)
选择后	\((1-s)p^2\)	\(2pq\)	\((1-t)q^2\)	\(T=1-sp^2-tq^2\)
相对频率	\(\cfrac{p^2}{T}\)	\(\cfrac{2pq}{T}\)	\(\cfrac{(1-s)q^2}{T}\)	\(1\)

带入式 \((1)\) 得，选择平衡时：

\[sp=tq \]

\[\therefore\begin{cases} p&=\cfrac{t}{s+t}\\ q&=\cfrac{s}{s+t} \end{cases} \]

3. 有迁移

\[\Huge\underset{\small P(a)=q_B}{\bigcirc}\xrightarrow{\normalsize m}\underset{\small P(a)=q_n}{\circ} \]

• 大种群足够大，\(q_B\) 不会变化
• 年迁移率 \(m=\cfrac{\textsf{迁来的个体数}}{\textsf{迁来的个体数}+\textsf{原来的个体数}}\)

法一

\[\begin{aligned} q_1&=mq_B+(1-m)q_0\\ q_2&=mq_B+(1-m)q_1\\ &=mq_B+(1-m)mq_B+(1-m)^2q_0\\ q_3&=mq_B+(1-m)q_2\\ &=mq_B+(1-m)mq_B+(1-m)^2mq_B+(1-m)^3q_0\\ \vdots\\ q_n&=mq_B\sum_{i=0}^{n-1}{(1-m)^i}+(1-m)^nq_0 \end{aligned} \]

小奥再次启动！

令 \(S=\displaystyle\sum_{i=0}^{n-1}{(1-m)^i}\)，\(a=1-m\)

\[\begin{aligned} S&=\sum_{i=0}^{n-1}{a^i}\\ aS&=\sum_{i=1}^{n}{a^i}\\ (a-1)S&=a^n-1\\ S&=\cfrac{a^n-1}{a-1}\\ &=\cfrac{(1-m)^n-1}{-m}\\ \therefore q_n&=q_B-(1-m)^nq_B+(1-m)^nq_0\\ \cfrac{q_n-q_B}{q_0-q_B}&=(1-m)^n \end{aligned} \]

这是什么？等比数列！

于是有了：

法二

\[\begin{aligned} q_1&=mq_B+(1-m)q_0\\ q_1-q_B&=mq_B+(1-m)q_0-q_B\\ q_1-q_B&=(1-m)(q_0-q_B)\\ \cfrac{q_1-q_B}{q_0-q_B}&=1-m\\ \Rightarrow \cfrac{q_n-q_B}{q_0-q_B}&=(1-m)^n \end{aligned} \]

光速出结论。

---

十分感谢你能看到这里。