前言
赛场上 \(\rm{while}\) 打成 \(\rm{if}\) 痛失 \(40 \rm{pts}\)
不过下来看是贪心的话也没什么好做的了, 一般都不会
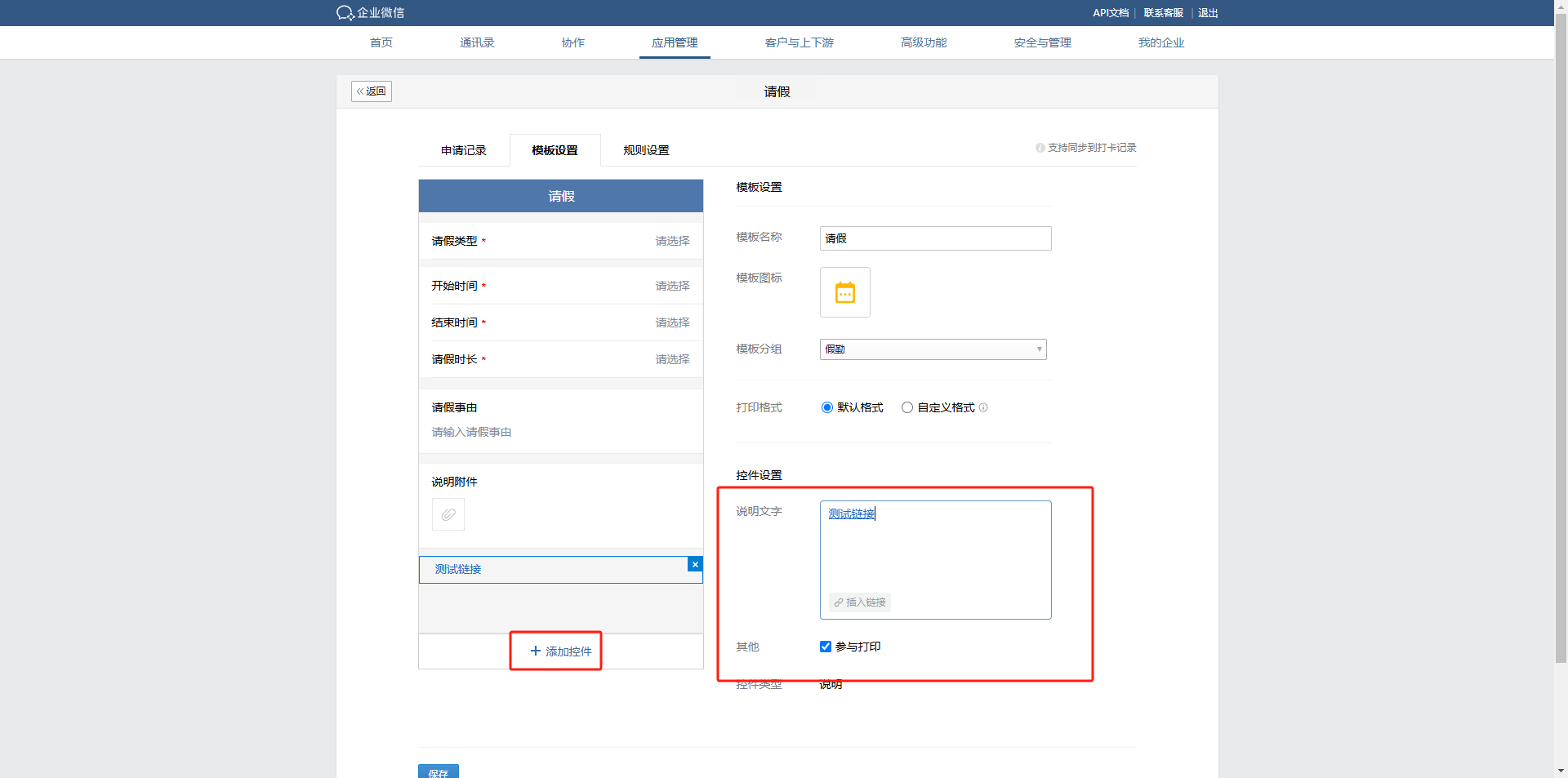
对了这是题目
题目下载
\(\rm{sol}\)
方法 \(1\) : 逐位计算
思路
显然的是你需要把数字从大到小填入, 使得高位的数尽量大, 这个显然
由上面的结论可以知道, 如果你从大到小考虑每一个数, 每个数填给 \(a, b\) 中的一个一定是符合最优解的构造的
考虑对于当前的数字, 填给 \(a, b\) 哪个更优
假设当前已经填过的前缀为 \(A, B\) , 显然的如果有一个的大小已经达标那么填给另一个
假设当前的数字为 \(x\) , 分类讨论计算贡献
- \(x\) 放给 \(A\) , \(A \gets 10A + x, AB = 10AB + Bx\)
- \(x\) 放给 \(B\) , \(B \gets 10B + x, AB = 10AB + Ax\)
发现什么?
两个贡献的形式都是 \(10AB + con\) , 而 \(AB\) 是上一次选择产生的贡献, 这证明了在这里使用贪心法使得填数之后当前贡献最大是正确的
对贡献作差, 结果是 \((B - A)x\) , 显然的
- \(B > A\) , 填给 \(a\)
- \(A > B\) , 填给 \(b\)
考虑 \(A = B\) 的情况
需要注意的是, 我们当前无论填给谁, 对之后的贡献都是 \(0\) , 所以这是一个全局性的考量
你发现一直填下去, 直到最后 \(A, B\) 有一个达到了 \(a, b\) 的要求, 那么接下来的贡献呢
我们钦定 \(a < b\) , 其他情况同理 (特别的, \(a = b\) 的时候可以随意填)
假设当前剩下的数为 \(x\) , 其位数为 \(b - a\)
记 \(A, B\) 前面位数相同的极大前缀为 \(A^{\prime}, B^{\prime}\)
\(\rm{belike}\) :

的黄色部分
最终的贡献柿子为
我们知道的是, \(x, A^{\prime}B^{\prime}\) 并不由当前选择填给谁而决定, 而 \(A^{\prime}, B^{\prime}\) 是受影响的
所以我们应当令 \(A^{\prime}\) 尽量大, 也就是说, 我们要把这个数填给位数较小的数
总结
善于通过计算单个单位的贡献来解决一类贪心问题
拍子可以搞出一些 \(\rm{border\ case}\) 去做, 时间充裕还是要打
对贡献作差是一种常见的方法来找到最优解
方法 \(2\) : 确定性
实现
首先是学习一下常用的高精度模板, 以后避免不会用
框架
首先 \(A, B\) 的比较和乘法都需要高精度, 让我来看看这两个怎么做
补好是两个高精度相乘, 我们没救了
代码
首先是高精度不想写了, 所以写 \(\rm{python}\)
#include <bits/stdc++.h>
#define int long long
const int MAXVAL = 10;
const int MAXN = 21;int T;
int a, b;
int num[MAXVAL];signed main()
{scanf("%lld", &T);while (T--) {int ans = 0;scanf("%lld %lld", &a, &b);for (int i = 1; i <= 9; i++) scanf("%lld", &num[i]);int A = 0, B = 0;int res = 9;int cnt = a + b;for (int i = 1; i <= cnt; i++) {while (!num[res] && res > 0) res--;if (a == 0) B = B * 10 + res, b--;else if (b == 0) A = A * 10 + res, a--;else if (B > A) A = A * 10 + res, a--;else if (A > B) B = B * 10 + res, b--;else {if (a < b) A = A * 10 + res, a--;else B = B * 10 + res, b--;}num[res]--;}printf("%lld\n", A * B);}return 0;
}