P10145 [WC2024] 线段树 题解
# P10145 [WC2024] 线段树 题解## $\mathcal O(4^{n})$ 做法对于线段树上的一个节点区间 $[l,r)$ 我们连无向边 $(l,r)$,那么可以用加减表示出一个区间 $[L,R)$ 等价于 $L,R$ 两点联通。于是可以枚举每条边选或不选,用可撤销并查集判断两点是否联通,复杂度 $\mathcal O(2^{2n-1}\alpha(n))\approx\mathcal O(4^n)$。## 特殊性质做法特殊性质就是整个图联通。对与线段树上的每个区间,令 $f_o,g_o$ 分别表示区间联通与不连通的方案数,有:$$
f_o=2f_{ls}f_{rs}+f_{ls}g_{rs}+f_{rs}g_{ls}\\
g_o=f_{ls}g_{rs}+f_{rs}g_{ls}
$$在“线段树”上转移即可。----------------------------------思路分界线---------------------------------------## $\mathcal O(n^2m)$ 做法因为我们不再需要让整个图联通,所以不能简单的记录是否联通,由于每次增加一个大区间,总是把最左边的与最右边的联通,所以我们记 $f_o$ 表示区间联通,$g_{o,j}$ 表示区间不连通且 左端点最远与 $j$ 联通的方案数,则:$$
\begin{aligned}
&f_{ls}f_{rs}\to f_o\\
&f_{ls}g_{rs,j}\to f_o,f_{ls}g_{rs,j}\to g_{o,j}\\
&g_{ls,j}f_{rs}\to f_o,g_{ls,j}f_{rs}\to g_{o,j}\\
&g_{ls,j}g_{rs,k}\to f_o,g_{ls,j}g_{rs,k}\to g_{o,j}
\end{aligned}
$$对于第四组转移,区间 $(j,k)$ 在也无法与外界联通,所以转移时要求每个需要确定的区间 $[L,R)$ 要么都在里面,要么都在外面。最后答案就是 $f_{root}+g_{root,i}$,其中 $i$ 满足每个 $[L,R)$ 要么都在 $[0,i)$ 里面,要么都在 $[0,i)$ 外面,直接转移+枚举 $[L,R)$ 做到 $\mathcal O(n^2m)$。## $\mathcal O(n^2)$ 做法对于每个 $[L,R)$ ,使用异或Hash,随机一个权值 $v$,$q_L\oplus v\to q_L,q_R\oplus v\to q_R$,最后令 $V$ 表示 $q$ 的前缀异或和,那么第四组的转移限制相当于要求 $V_j=V_k$,这样避免了直接枚举限制。## $\mathcal O(n\log n)$ 做法直接将转移中的 $j$ 替换成 $V_j$ 那么转移变成了:$$
\begin{aligned}
&f_{ls}f_{rs}\to f_o\\
&f_{ls}g_{rs,j}\to f_o,f_{ls}g_{rs,j}\to g_{o,j}\\
&g_{ls,j}f_{rs}\to f_o,g_{ls,j}f_{rs}\to g_{o,j}\\
&g_{ls,j}g_{rs,j}\to f_o,g_{ls,j}g_{rs,j}\to g_{o,j}
\end{aligned}
$$可以用线段树合并解决,复杂度 $\mathcal O(n\log n)$。## 参考[笋 - 洛谷专栏](https://www.luogu.com.cn/article/gxwwzkhd)
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.hqwc.cn/news/863816.html
如若内容造成侵权/违法违规/事实不符,请联系编程知识网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!相关文章
EXCEL中自动突出显示(自动高亮)行或列
EXCEL中,当选择的单元格距离列首或行首过远时,考验眼睛的时候就到了。解决方法很多,如果想要自动突出显示,就只能上vba代码了。解决的问题
EXCEL中,当选择的单元格距离列首或行首过远时,考验眼睛的时候就到了。解决方法很多,如果想要自动突出显示,就只能上vba代码了。方…
DL00868-基于深度学习的红外船舶检测识别分类完整实现数据8000+
随着遥感技术的快速发展,包括无人机、卫星等,红外图像在船舶检测识别中的作用日益凸显。相对于可见光图像,红外图像具有在夜晚和恶劣天气条件下高效检测识别船舶的天然优势。近年来,深度学习作为一种强大的图像处理技术,在红外船舶检测识别领域取得了显著进展。完整链接:…
基于深度学习的红外船舶检测识别分类完整实现数据集8000+张
随着遥感技术的快速发展,包括无人机、卫星等,红外图像在船舶检测识别中的作用日益凸显。相对于可见光图像,红外图像具有在夜晚和恶劣天气条件下高效检测识别船舶的天然优势。近年来,深度学习作为一种强大的图像处理技术,在红外船舶检测识别领域取得了显著进展。完整链接:…
第三章 MBR -- loader
第三章 MBR --> loader
本文是对《操作系统真象还原》第三章学习的笔记,欢迎大家一起交流。
a
知识介绍
在上一章的代码部分,我们通过 BIOS 中断进行字符输出,但是离开实模式之后,BIOS 中断就没法用了,因为 BIOS 中断向量表只在实模式下存在,因此我们肯定还会有别的方…
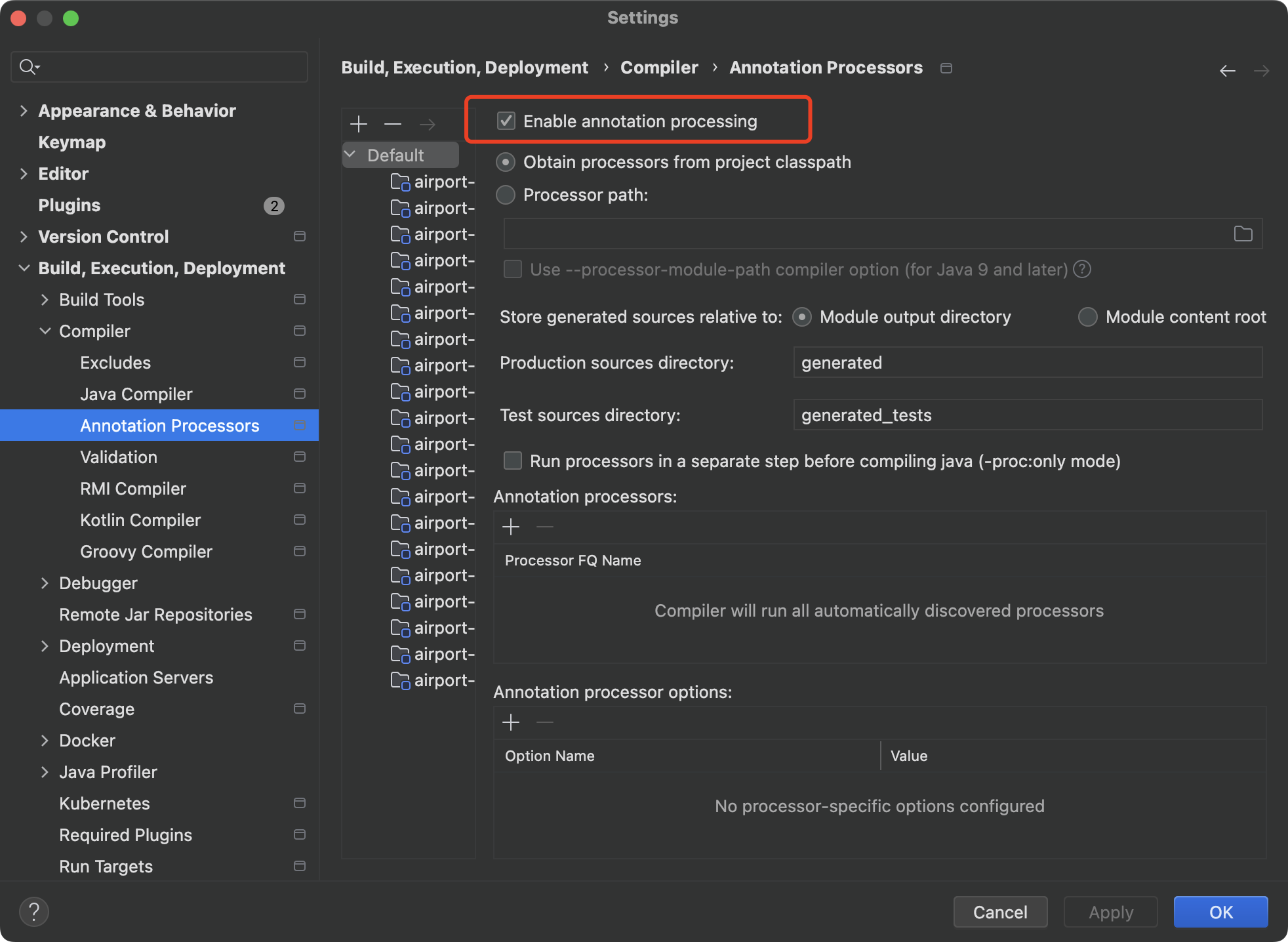
itextpdf 找出PDF中 文字的坐标
目录添加引用添加工具类调用
找到位置,签名的话见:https://www.cnblogs.com/vipsoft/p/18644127
新项目可以尝试一下 iText 7 , 我这边是老项目所以还是继续使用 iText 5,主打够用
iText 5 没有直接提供获取文本精确位置的功能。它只能提取文本内容,而文本位置通常需要通过…
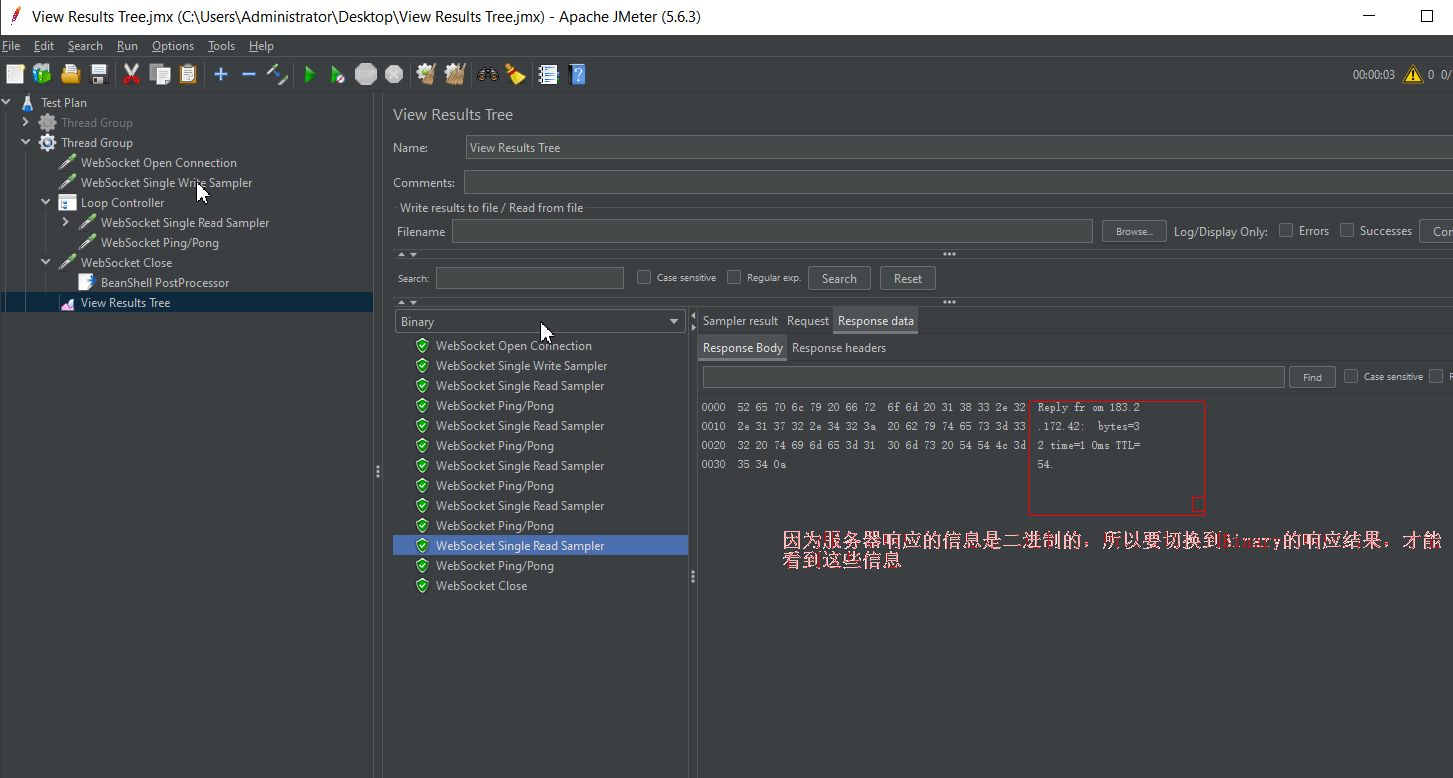
Jmeter 进行websocket接口测试
什么是websocket协议?
Websocket是基于tcp的一种全双通信协议,客户端与服务器之间通过websocket建立连接后,客户端和服务器之间会长时间保持连接状态(即长连接)。客户端可以向服务器发送数据,服务器也可以主动向客户端推送数据。与http协议不同的是http是tcp的单向通信协…
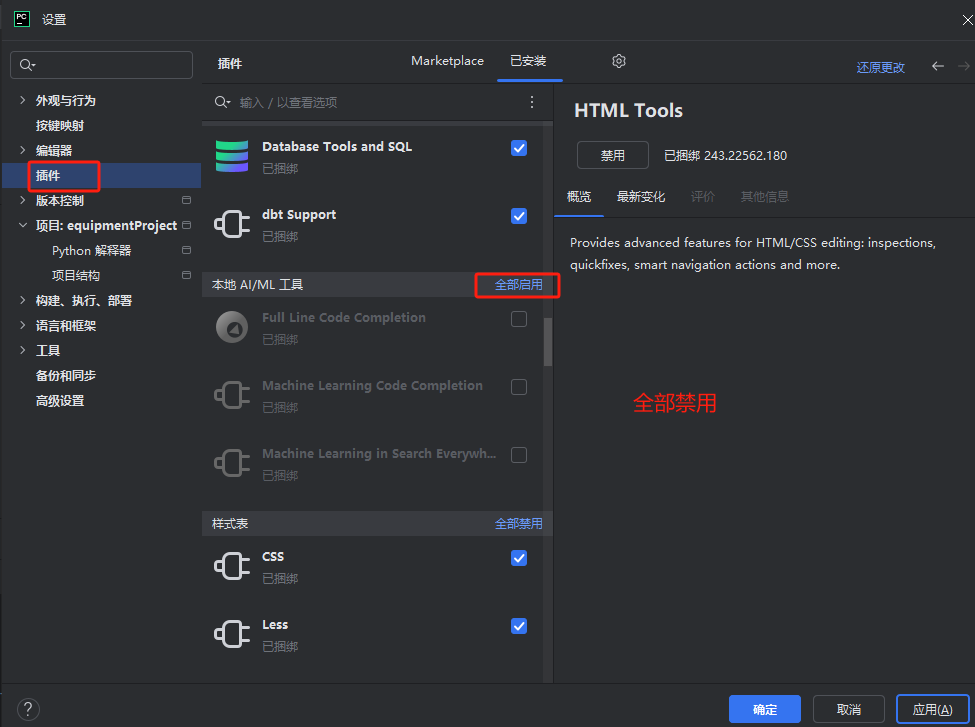
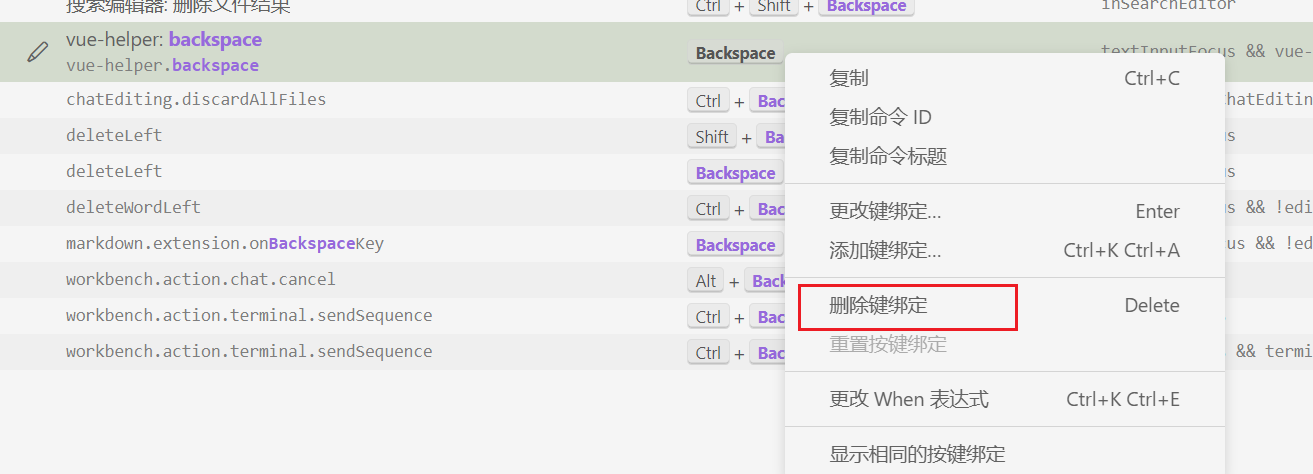
vscode下载vetur和vue-helper插件之后删除键(backspace)失效
最近我在学习前端的过程中,使用vscode下载的vue的插件:vetur和vue-helper这两个
但随后在写代码的时候发现删除键(backspace)不能使用,其他键都能正常使用,也可以用鼠标选中右键剪切/删除
最后发现是上面的插件会占用backspace按键作为插件的功能键
解决方法
点击左上角—…
使用 C# WPF 根据 SEGY 数据绘制二维地震图
一、引言
在地震勘探领域,SEGY(Society of Exploration Geophysicists Y-data)文件格式是常见的地震数据存储格式。对于地震数据的可视化,通常会将 SEGY 文件中的振幅数据通过图像进行展示,以便进行分析。本文将介绍如何使用 C# WPF 应用程序绘制基于 SEGY 数据的二维地震…
为什么浏览器打开的网页默认是英文显示?
最近在学习的时候遇到的问题,打开一些软件的官网默认都是英文(即使这些网站是国内做的)。
其中一个原因是浏览器的默认设置语言是英文
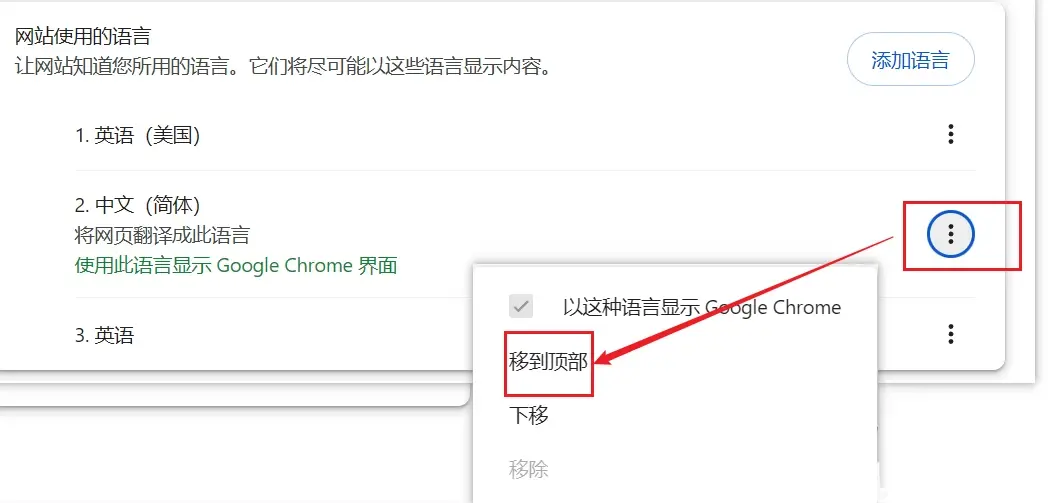
修改浏览器默认语言
以Google Chrome浏览器为例:
右上角三个点—>设置
左边找到“语言”
将中文置顶
LeetCode 762[二进制表示中质数个计算置位]
LeetCode 762[二进制表示中质数个计算置位]题目
链接
LeetCode 762[二进制表示中质数个计算置位]
详情实例提示题解
思路
两个条件:
1、二进制位为1
2、满足条件1的个数为质数首先 for 循环遍历区间for (int i = left; i < right + 1; i++){int iCount = 0;//二进制位为1的…




![LeetCode 762[二进制表示中质数个计算置位]](https://img2024.cnblogs.com/blog/3512406/202501/3512406-20250104105904683-1815538611.png)