Z变换的性质-编程知识

Z变换的性质

news/2025/1/6 19:32:43/文章来源:https://www.cnblogs.com/codersgl-blog/p/18652524

名称	时域 $f(k)$	Z域 $F(z)$
线性	$a_1 f_1(k) + a_2 f_2(k)$	$a_1 F_1(z) + a_2 F_2(z)$
移序（移位）性	$f(k+m) \quad (m > 0)$	$z^m F(z) - \sum_{k=0}^{m-1} f(k) z^{m-k-1}$
	$f(k-m)u(k-m) \quad (m > 0)$	$z^{-m} F(z)$
比例性（尺度变换）	$a^k f(k)$	$F\left(\frac{z}{a}\right)$
Z域微分	$k f(k)$	$-z \frac{dF(z)}{dz}$
Z域积分	$\frac{1}{k} f(k) \quad (a > 0)$	$\int_{z}^{\infty} F(v) v^{-(a+1)} dv$
时域卷积	$f_1(k) * f_2(k)$	$F_1(z) F_2(z)$
时域相乘	$f_1(k) \cdot f_2(k)$	$\frac{1}{2\pi j} \oint_C F_1(v) F_2\left(\frac{z}{v}\right) \frac{dv}{v}$
序列求和	$\sum_{n=0}^{\infty} f(n)$	$\frac{z}{z-1} F(z)$
初值定理	$f(0) = \lim_{z \to \infty} F(z)$
	$f(m) = \lim_{z \to \infty} z^m \left[ F(z) - \sum_{k=0}^{m-1} f(k) z^{-k} \right]$
终值定理	$f(\infty) = \lim_{z \to 1} (z-1) F(z)$

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.hqwc.cn/news/864056.html

如若内容造成侵权/违法违规/事实不符，请联系编程知识网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

已读乱回

我将safetensors格式的TableGPT2-7B通过llama.cpp转换成gguf

python-selenium (1、配置环境)

准备如下： 1、python以及开发工具PyCharm 2、浏览器以及对应的浏览器驱动 3、下载selenium工具包注意: 浏览器与浏览器驱动需要版本一致，以goole为例, https://googlechromelabs.github.io/chrome-for-testing/known-good-versions-with-downloads.json 这个网站里面有对应谷…

12306分流抢票软件 bypass v1.16.43 绿色版（春节自动抢票工具）

软件介绍 12306Bypass分流抢票软件，易操作强大的12306抢票软件，全程自动抢票，云识别验证码打码，多线程秒单、稳定捡漏，支持抢候补票、抢到票自动付款，支持多天、多车次、多席别、多乘客、短信提醒等功能。1、Bypass分流抢票本身附带云识别模块帮助识别，但实际测试即便是…

网络_浏览器的通信能力

本文主要介绍了浏览器的通信能力，包括用户代理、AJAX，在用户代理中浏览器具有自动发送请求的能力和自动解析响应的能力；在AJAX中主要有两种实现方式，分别是XMLHttpRequest和Fetch；另外介绍了XML可以监控请求进度可用于文件上传进度的监控，Fetch更擅长处理异步代码具有流的…

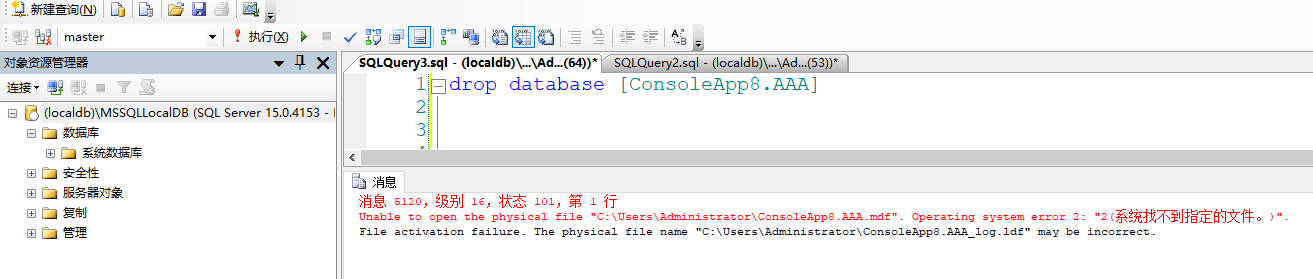
$(LocalDB)\MSSQLLocalDB相关$

系统数据库路径：C:\Users\Administrator\AppData\Local\Microsoft\Microsoft SQL Server Local DB\Instances\MSSQLLocalDB 用户数据库默认路径：C:\Users\Administrator 连接字符串：<connectionStrings><add name="AAA" connectionString="data sou…

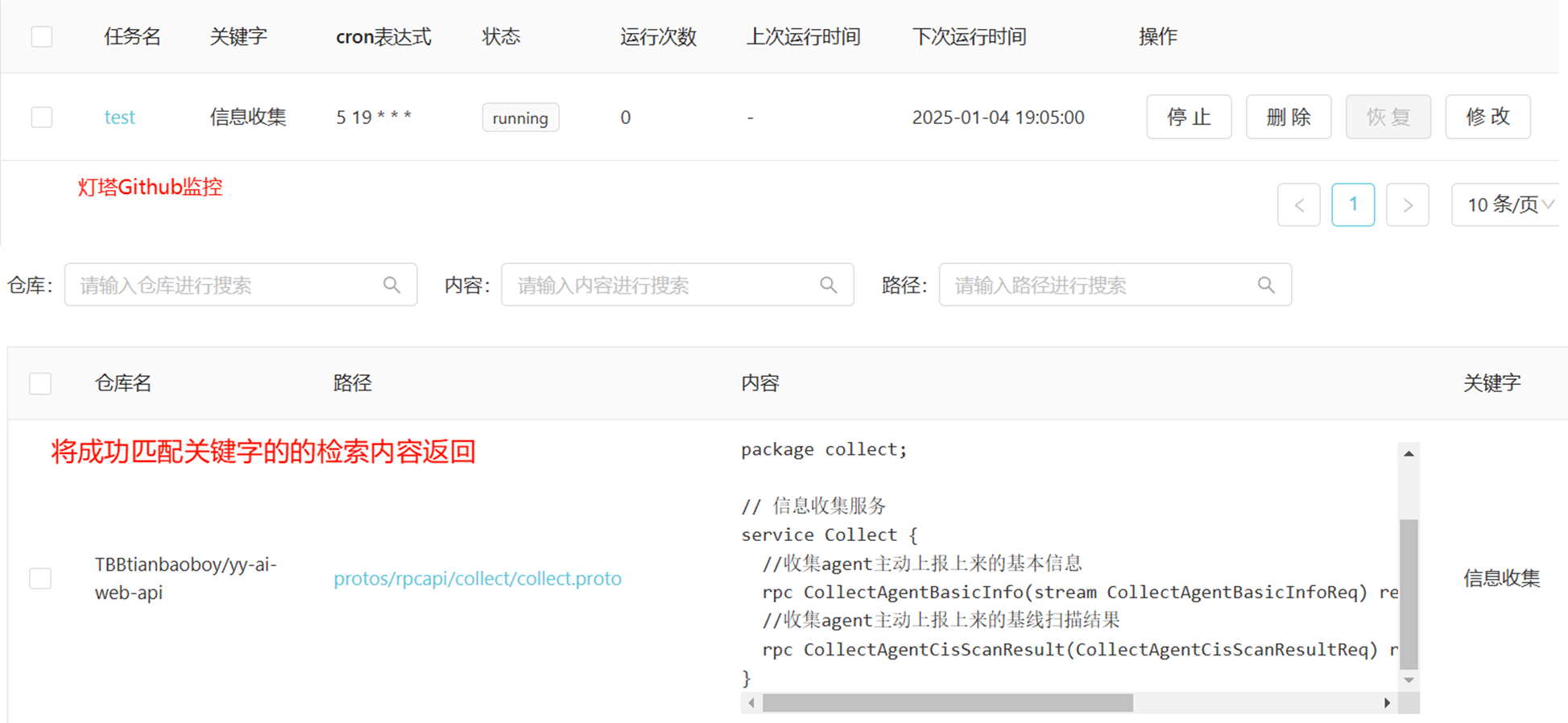
Mind（信息收集篇）

对于在信息收集中所学习知识点做一总结。免责声明：本文章仅用于交流学习，因文章内容而产生的任何违法&未授权行为，与文章作者无关！！！附：完整笔记目录~ ps：本人小白，笔记均在个人理解基础上整理，若有错误欢迎指正！七、Mind（信息收集篇）

VOLTE中eSRVCC相关的一些知识点

注：本文中的SRVCC都是指eSRVCC方案。 SRVCC相关的3GPP规范有：3GPP TS 23.216 SRVCC 3GPP TS 23.856 “Single Radio Voice Call Continuity (SRVCC) enhancement; Stage2.” 3GPP TS 23.237 IMS Service Continuity Stage 2 3GPP TS 24.237 IMS Service Continuity Stage 3详…

信息收集补充思路

引子：前几章分别介绍了针对不同目标的信息收集内容&方式&工具，本章内容则并非针对某一具体目标，而是对前几章信息收集思路&方式的补充。免责声明：本文章仅用于交流学习，因文章内容而产生的任何违法&未授权行为，与文章作者无关！！！附：完整笔记目录~ p…

JVM实战—10.MAT的使用和JVM优化总结

大纲 1.线上大促活动导致的老年代内存泄漏和FGC(MAT分析出本地缓存没处理好) 2.百万级数据误处理导致频繁FGC(大数据量加载到内存处理 + String.split()) 3.JVM运行原理和GC原理总结 4.JVM性能优化的思路和步骤 5.问题汇总1.线上大促活动导致的老年代内存泄漏和FGC(MAT分析出本…

请问数据库迁移后无法登录的问题及解决方案

数据库迁移后无法登录的问题可能由多种原因引起，特别是在迁移过程中涉及到数据库结构、权限设置或配置文件的变化。为了确保顺利迁移并解决登录问题，您可以按照以下步骤进行排查和处理：确认迁移完整性：首先，确保数据库迁移过程完整无误。检查迁移工具的日志，确认所有表、…

名称	时域 \(f(k)\)	Z域 \(F(z)\)
线性	\(a_1 f_1(k) + a_2 f_2(k)\)	\(a_1 F_1(z) + a_2 F_2(z)\)
移序（移位）性	\(f(k+m) \quad (m > 0)\)	\(z^m F(z) - \sum_{k=0}^{m-1} f(k) z^{m-k-1}\)
	\(f(k-m)u(k-m) \quad (m > 0)\)	\(z^{-m} F(z)\)
比例性（尺度变换）	\(a^k f(k)\)	\(F\left(\frac{z}{a}\right)\)
Z域微分	\(k f(k)\)	\(-z \frac{dF(z)}{dz}\)
Z域积分	\(\frac{1}{k} f(k) \quad (a > 0)\)	\(\int_{z}^{\infty} F(v) v^{-(a+1)} dv\)
时域卷积	\(f_1(k) * f_2(k)\)	\(F_1(z) F_2(z)\)
时域相乘	\(f_1(k) \cdot f_2(k)\)	\(\frac{1}{2\pi j} \oint_C F_1(v) F_2\left(\frac{z}{v}\right) \frac{dv}{v}\)
序列求和	\(\sum_{n=0}^{\infty} f(n)\)	\(\frac{z}{z-1} F(z)\)
初值定理	\(f(0) = \lim_{z \to \infty} F(z)\)
	\(f(m) = \lim_{z \to \infty} z^m \left[ F(z) - \sum_{k=0}^{m-1} f(k) z^{-k} \right]\)
终值定理	\(f(\infty) = \lim_{z \to 1} (z-1) F(z)\)