文章目录
- 74. 搜索二维矩阵:
- 样例 1:
- 样例 2:
- 提示:
- 分析:
- 题解:
- rust:
- go:
- c++:
- python:
- java:
74. 搜索二维矩阵:
给你一个满足下述两条属性的 m x n 整数矩阵:
- 每行中的整数从左到右按非递减顺序排列。
- 每行的第一个整数大于前一行的最后一个整数。
给你一个整数 target ,如果 target 在矩阵中,返回 true ;否则,返回 false 。
样例 1:

输入:matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3输出:true
样例 2:
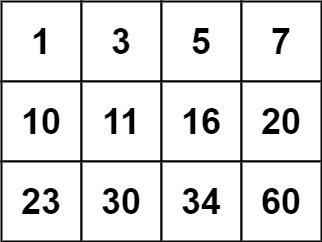
输入:matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 13输出:false
提示:
- m == matrix.length
- n == matrix[i].length
- 1 <= m, n <= 100
- -104 <= matrix[i][j], target <= 104
分析:
- 面对这道算法题目,二当家的再次陷入了沉思。
- 在有序列表中,查找指定元素,一般使用二分查找,非常高效。
- 但是题目中是个二维矩阵,是否还能用二分查找呢?
- 首先想到,可以用两次二分查找,分别看在哪行,再看在哪列,效率已经很高了,但是是否能只用一次二分查找呢?
- 想要使用一次二分查找,就需要将二维矩阵转换成线性结构,有什么办法呢?
- 我们可以快速算出矩阵的长和宽,也就可以拿到它的总长度,我们可以快速将长度范围内的下标,快速转换成行和列的下标,因为行列都是等长的。
题解:
rust:
impl Solution {pub fn search_matrix(matrix: Vec<Vec<i32>>, target: i32) -> bool {let (m, n) = (matrix.len(), matrix[0].len());let (mut left, mut right) = (0, m * n);while left < right {let mid = left + ((right - left) >> 1);let v = matrix[mid / n][mid % n];if v < target {left = mid + 1;} else if v > target {right = mid;} else {return true;}}return false;}
}
go:
func searchMatrix(matrix [][]int, target int) bool {m, n := len(matrix), len(matrix[0])i := sort.Search(m*n, func(i int) bool { return matrix[i/n][i%n] >= target })return i < m*n && matrix[i/n][i%n] == target
}
c++:
class Solution {
public:bool searchMatrix(vector<vector<int>>& matrix, int target) {const int m = matrix.size(), n = matrix[0].size();int left = 0, right = m * n;while (left < right) {const int mid = left + ((right - left) >> 1);const int v = matrix[mid / n][mid % n];if (v < target) {left = mid + 1;} else if (v > target) {right = mid;} else {return true;}}return false;}
};
python:
class Solution:def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:m, n = len(matrix), len(matrix[0])left, right = 0, m * nwhile left < right:mid = left + ((right - left) >> 1)v = matrix[mid // n][mid % n]if v < target:left = mid + 1elif v > target:right = midelse:return Truereturn Falsejava:
class Solution {public boolean searchMatrix(int[][] matrix, int target) {final int m = matrix.length, n = matrix[0].length;int left = 0, right = m * n;while (left < right) {final int mid = left + ((right - left) >> 1);final int v = matrix[mid / n][mid % n];if (v < target) {left = mid + 1;} else if (v > target) {right = mid;} else {return true;}}return false;}
}
非常感谢你阅读本文~
欢迎【点赞】【收藏】【评论】三连走一波~
放弃不难,但坚持一定很酷~
希望我们大家都能每天进步一点点~
本文由 二当家的白帽子:https://le-yi.blog.csdn.net/ 博客原创~