HDU7521 cats 的二分答案 题解

思路

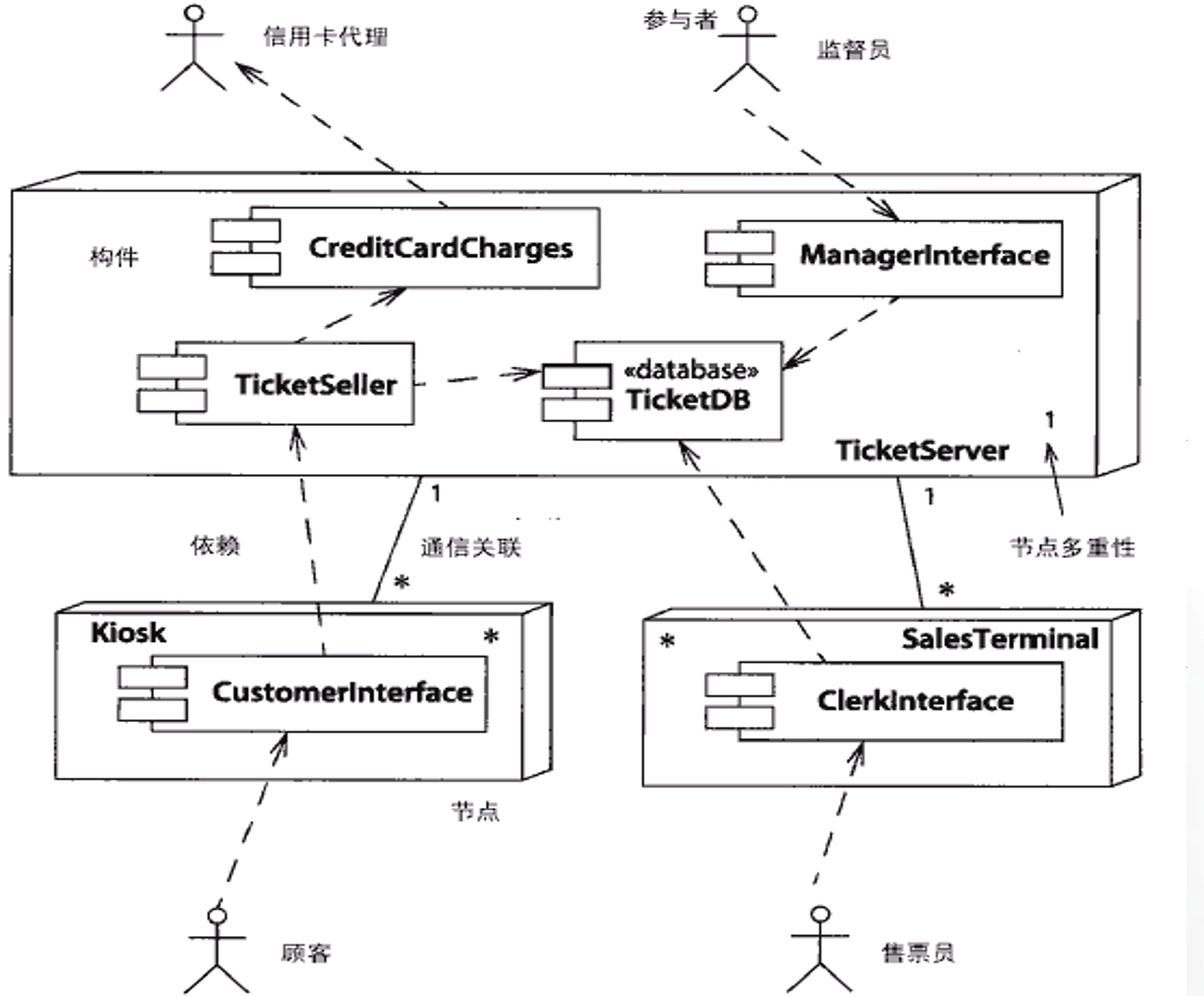
首先，转换一下题意。只有在 \(val = 0\) 时，才会向左缩小范围。

然而只有越界访问才能达成 \(val = 0\)，因此实际上我们最多只能向左缩小范围 \(k\) 次。

对于当前的二分区间，\(mid\) 本身可以作为一个答案，同时还要加上左右两边子区间的贡献。因此想到可以递归计算子区间的贡献。

考虑对于同样长度、\(k\) 相等的区间，其答案应该是一样的。因此我们不用考虑具体的左右端点，只用考虑区间长度和 \(k\) 即可。

加上记忆化搜索优化时间。

AC 代码

#include<bits/stdc++.h>
using namespace std;
long long t;
long long x,y,n;
map<pair<long long,long long>,long long> Map;
long long getans(long long len,long long k){if(len <= 0){return 0;}if(len == 1){return 1;}if(k == 0){return log2(len)+1;}if(Map[{len,k}]){return Map[{len,k}];}long long mid = (len+1)>>1,res = 0;res++;res += getans(mid-1,k-1);res += getans(len-mid,k);Map[{len,k}] = res;return res;
}
int main(){scanf("%lld",&t);while(t--){Map.clear();scanf("%lld%lld%lld",&x,&y,&n);if(n > 66){printf("%lld\n",y-x+1);continue;}printf("%lld\n",getans(y-x+1,n));}return 0;
}