-
[题目链接](149. 直线上最多的点数 - 力扣(LeetCode))
-
解题思路:两个for循环。某一条直线,必须经过第一个点,最多经过多少点?某一条直线,必须经过第二个点,最多经过多少个点?以此类推,最多的那个结果,就是答案。
- 怎么知道必须经过某个点的【直线】,最多经过多少点?例如现在必须经过的点是
(x, y),我们只需要计算这个点和其他点的斜率即可。斜率还有一个问题,两个点,横坐标相同时,怎么办?纵坐标相同时,又怎么办?看代码具体处理。 - 还有一个细节,当处理j个点时,不必再看
[0, j - 1]的点了,为什么?假设最优解是同时经过j与i(i < j)的直线,我们在计算i的点时,已经计算过,【同时经过i和j】的直线了。
- 怎么知道必须经过某个点的【直线】,最多经过多少点?例如现在必须经过的点是
-
代码
class Solution:class twoPointRelation():def __init__(self, x, y, same):self.x = x # 斜率的分母self.y = y # 斜率的分子self.same = same # 为True,代表分母或者分子为0 分母为0时:x为0,y就是两个点的x轴的值, 分子为0时:y为0,x就是两个点y轴的值# 下面这两个函数是为了在字典的keydef __hash__(self):return hash((self.x, self.y, self.same))def __eq__(self, other):return self.same == other.same and self.x == other.x and self.y == other.ydef gcd(self, a, b):if b == 0:return areturn self.gcd(b, a % b)def maxPoints(self, points: List[List[int]]) -> int:# 两个点的关系:斜率k,(y1 - y2) / (x1 - x2) 当x相同时 没有斜率dict = {}count = len(points)ans = 0for i in range(count):dict.clear()for j in range(i + 1, count):x1 = points[i][0]y1 = points[i][1]x2 = points[j][0]y2 = points[j][1]first = y2 - y1 # 分子second = x2 - x1 # 分母if second == 0: # 分母为0k = self.twoPointRelation(0, x2, True)elif first == 0: # 分子为0k = self.twoPointRelation(y1, 0, True)else:num = self.gcd(first, second)k = self.twoPointRelation(second / num, first / num, False)if k in dict:dict[k] += 1else :dict[k] = 1ans = max(ans, dict[k])return ans + 1
149. 直线上最多的点数
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.hqwc.cn/news/866057.html
如若内容造成侵权/违法违规/事实不符,请联系编程知识网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!相关文章
2025.1.8 鲜花
Nim 的变种Nim 的变种グランドエスケープ
空飛ぶ羽根と引き換えに 繋ぎ合う手を選んだ僕ら
没有选择飞翔的翅膀 而是选择十指相扣的我们
それでも空に魅せられて 夢を重ねるのは罪か
却仍然向往着天空 反复做着同样的梦 这有错吗
夏は秋の背中を見て その顔を思い浮かべる
夏…
CTF 之 Crypto (Cryptography) 学习笔记
CTF 之 Crypto (Cryptography)
Chapter 0. 前置知识
群 (Group)
给定一个集合 \(G\neq \emptyset\) 以及二元代数运算 \(\circ\),若满足:封闭性 (Closure):\(\forall u,v\in G\),\(u\circ v\in G\);
结合律 (Associativity):\(\forall u,v,w\in G\),\((u\circ v)\circ w…
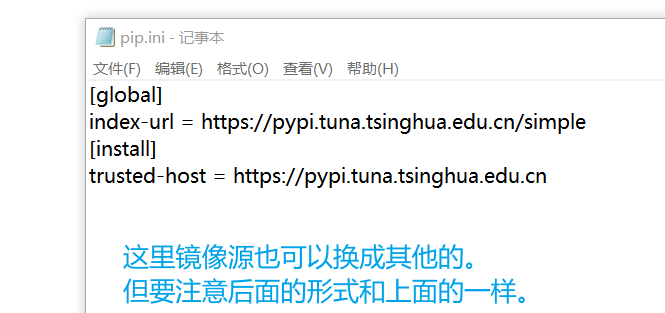
(2025自测有效!)全网最好的python配置教程【非常非常适合小白】
前几天我的电脑刚刚重装,把python重新配置了一下。
1.Python环境部署Python3 可应用于多平台包括 Windows、Linux 和 Mac OS X。
Python官网:https://www.python.org/
进入官网在导航栏选择Dowmloads,选择所使用的系统(以Windows为例)
进入Windows下载页之后选择需要下载的…
写一个支持折叠、有缩进、代码高亮、离线的,方便部署的、易用的、优雅的json格式化查看工具(附html完整代码)
缘由
网上的在线json格式化有很多,但我是个有追求的人。在线的很难同时支持折叠、有缩进线、代码高亮、离线的,方便部署的、易用的、不请求后端(为了安全)的json格式化工具。
去Github上找项目,华而不实的东西占半个屏幕,格式化json要点好几下,一个json格式化工具npm安装…
AGC041F Histogram Rooks
我不知道啊,我只是觉得容斥很好玩。一个朴素的想法是容斥:考虑钦定 \(S\) 集合的位置没有被车覆盖,则答案是 \((-1)^{|S|}2^{c}\),其中 \(c\) 是可以放车的位置,可以直接 dp 做到 \(\mathrm{O}(2^n \text{poly}(n))\),但是难以优化。
延续容斥的想法,注意到钦定一个位置…
rust学习十六.1、并发-乱弹和一个简单并发例子
如书本作者所言,并发编程在绝大部分语言中,都是相对复杂和困难的。
所以,涉及的内容会相对多一些,所涵盖的内容绝对不是几篇文章所可以容纳的。
权当一个乱弹琴!
和此系列的其它文章一样,本文的内容绝大部分来自于相关书籍,本人做了一些摘裁的工作,取我所需!一、无畏并…
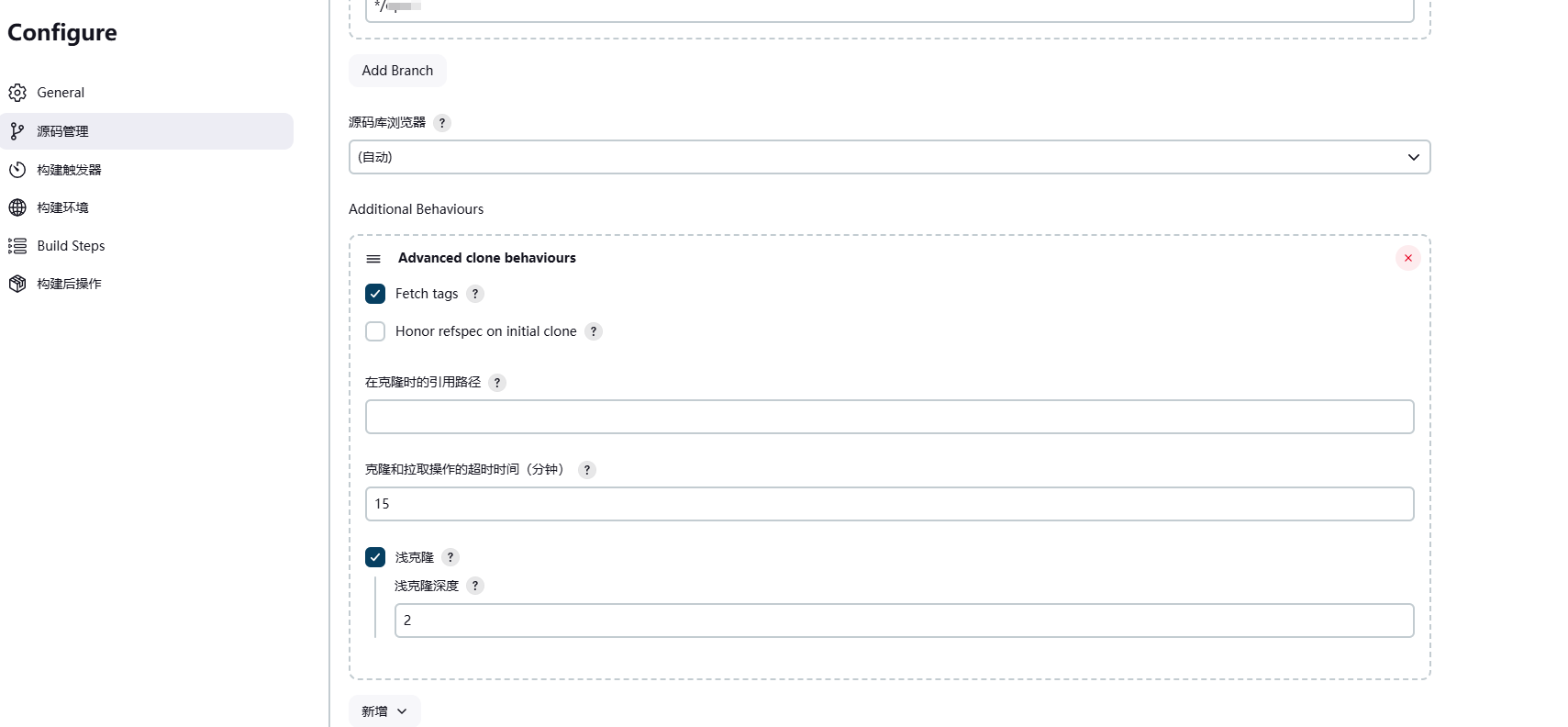
解决jenkins git 拉取代码超时问题
jenkins默认的是时间是10分钟,在git fetch时候超过10分钟了就报错失败了,可在项目源码管理 新增 advance clone behaviours
Java Bluetooth 蓝牙通讯 BlueCove 扫描附近的蓝牙设备
目录BlueCove项目概述BlueCove API架构API的设计原则和实现方式关键类和方法的功能描述测试代码获取本机(PC)蓝牙扫描蓝牙
BlueCove项目概述
BlueCove是一个开源的蓝牙协议栈实现,旨在为Java开发者提供一个全面的、易于使用的API,从而在应用程序中实现蓝牙功能。该项目支持多…
英伟达世界基础模型 Cosmos,教 AI 理解物理世界;阿里通义与雷鸟合作推出 AI 眼镜丨 RTE 开发者日报
开发者朋友们大家好:这里是 「RTE 开发者日报」 ,每天和大家一起看新闻、聊八卦。我们的社区编辑团队会整理分享 RTE(Real-Time Engagement) 领域内「有话题的新闻」、「有态度的 观点 」、「有意思的 数据 」、「有思考的 文章 」、「有看点的 会议 」,但内容仅代表编辑的…
.NET 窗口置于最顶层
本文介绍如何将窗口置于最顶层,以及解决在顶层显示时对锁屏登录界面的影响。用于实现类似Launcher、系统工具等应用需要窗口层级比Windows开始菜单以及置顶任务栏还要高的场景
一般情况下的窗口置顶,可以设置WPF窗口属性Topmost=true
也可以使用WIN32-SetWindowPos函数SetWin…
汽修行业的智能化转型:AI赋能员工培训SOP策略
随着智能化技术的飞速发展,汽修行业也迎来了前所未有的变革机遇。在这一背景下,如何构建高效、标准化的员工培训SOP(Standard Operating Procedure)策略,成为汽修企业提升竞争力、实现智能化转型的关键。本文将探讨智能AI在汽修行业员工培训SOP策略构建中的应用,特别是提…