【模拟电子技术】02-PN结的形成

半导体就是导电能力介于导体和半导体之间的东西, 本征半导体即纯净的半导体。
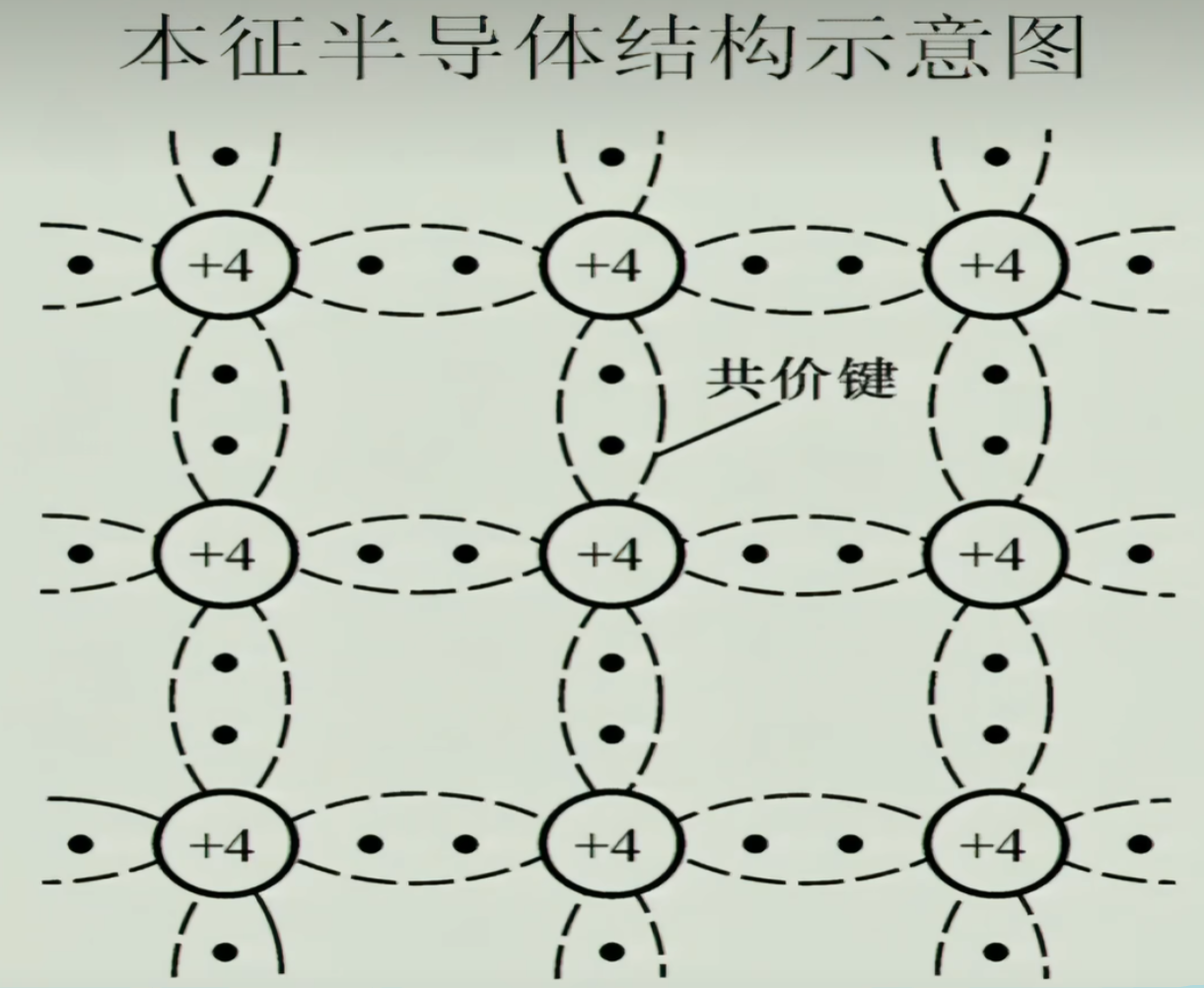
导电靠自由电子,可看到自由电子即使是本征激发也少,导电能力也不够。自由电子撞在空穴中,就是复合(与本征激发相反),两者发生的频率决定着载流子的浓度,其实是温度的改变决定着载流子浓度变化,T1变到T2的过程中,浓度变化显著,但稳定到T2后,本征激发与复合的速率逐渐平衡,浓度才逐渐稳定。但是这种现象究竟有什么用呢?即使我们给本征半导体加热,导电能力也上不去。作为时间穿越者的角度来看,我们直接用前人的办法:掺杂

P为5价,电子多,所以是N型,Negative,电子为多子,空穴是少子,少子有可能比本征半导体中的更少。温度导致的热运动对多子影响小,因为掺杂的半导体中多子数量本就很多,热运动再发生,加多的和掺杂进来的也不在一个数量级。相反对于少子来说,温度变化导致热运动产生的少子数量的变化在总体中就变得显著了。
B为3价,空穴为多子,掺入后为P型半导体,Positive。但是这样掺杂后有什么用呢,导电能力还是不如导体,我们把两种掺杂的半导体放在一起就会得到一个神奇的PN结
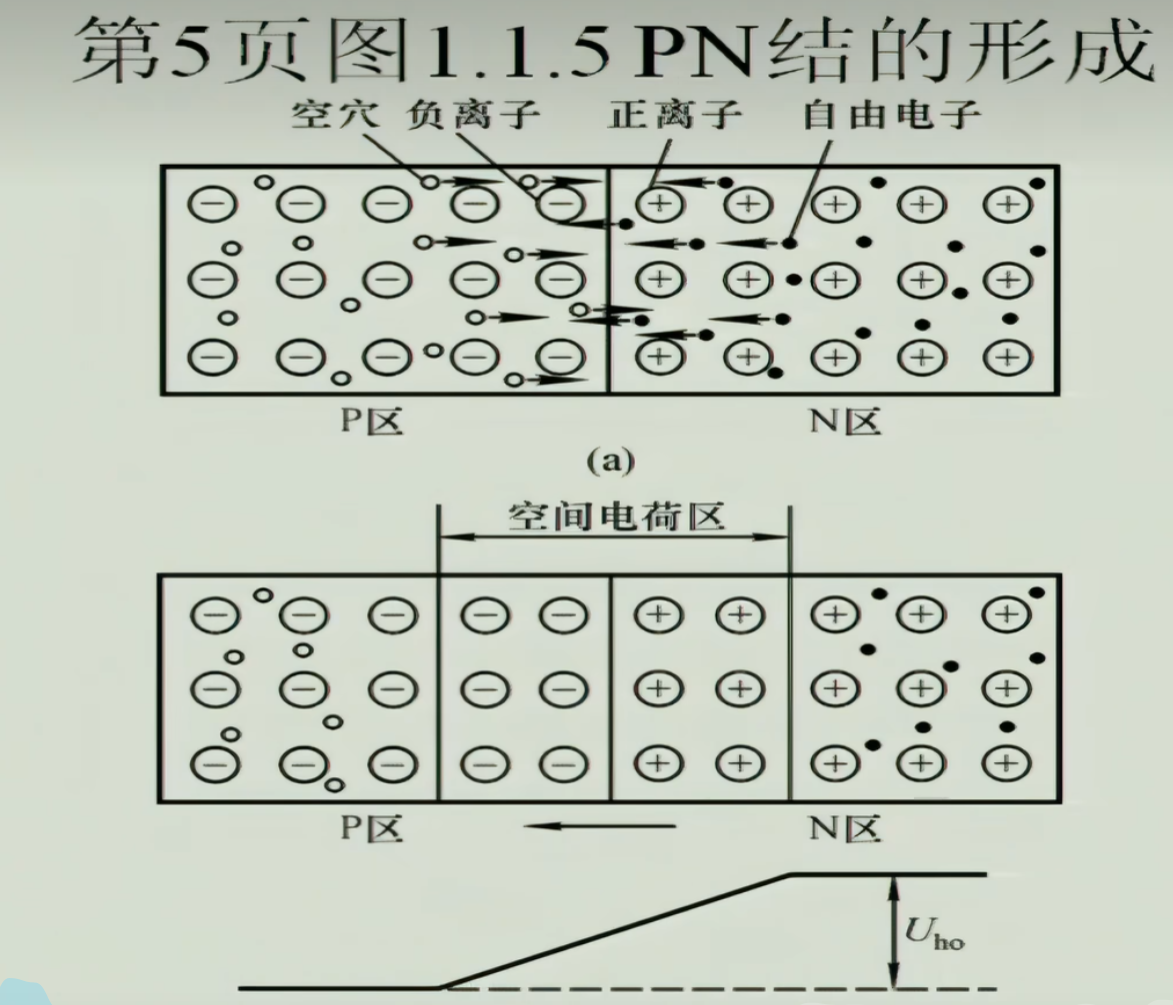
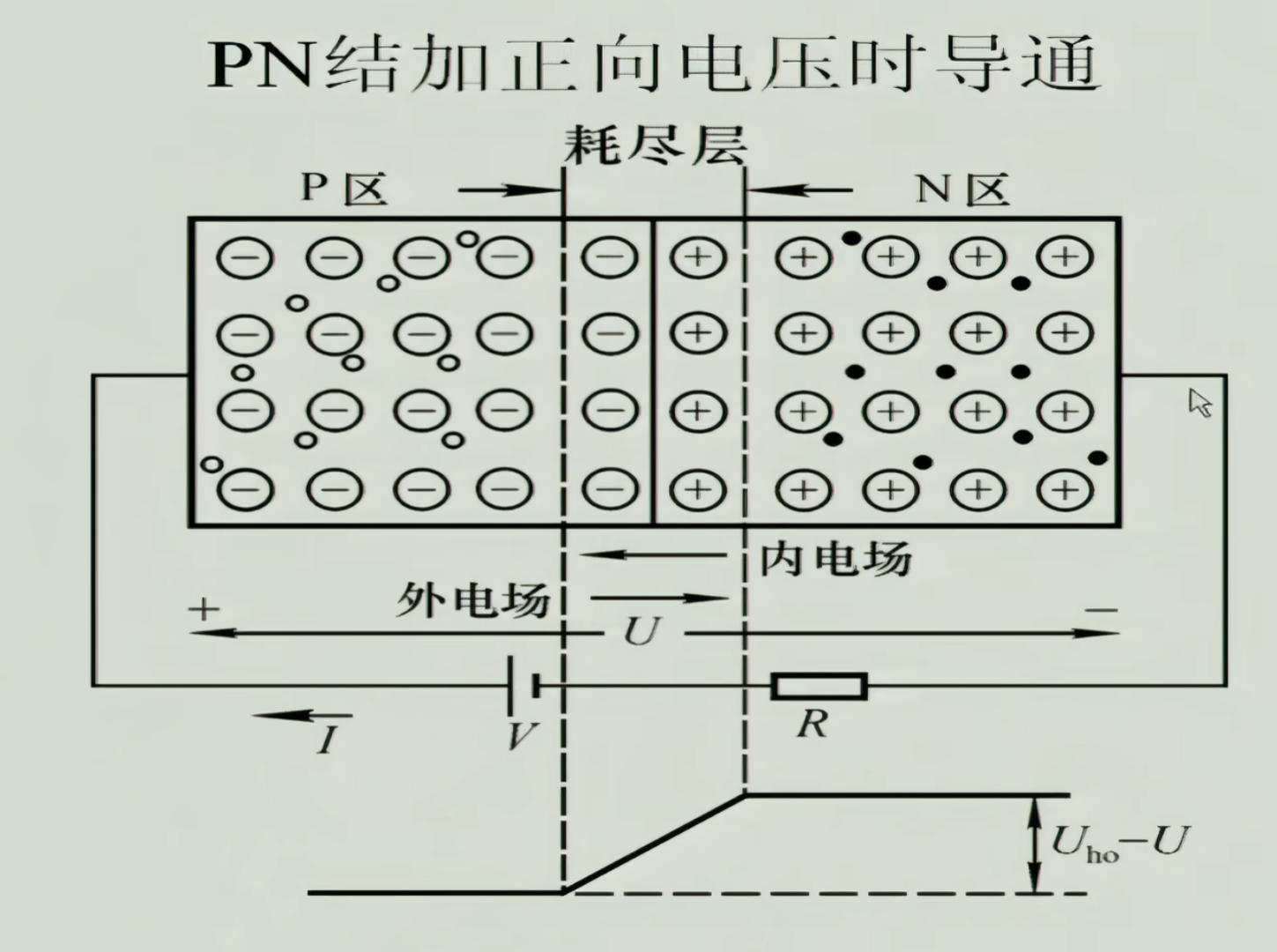
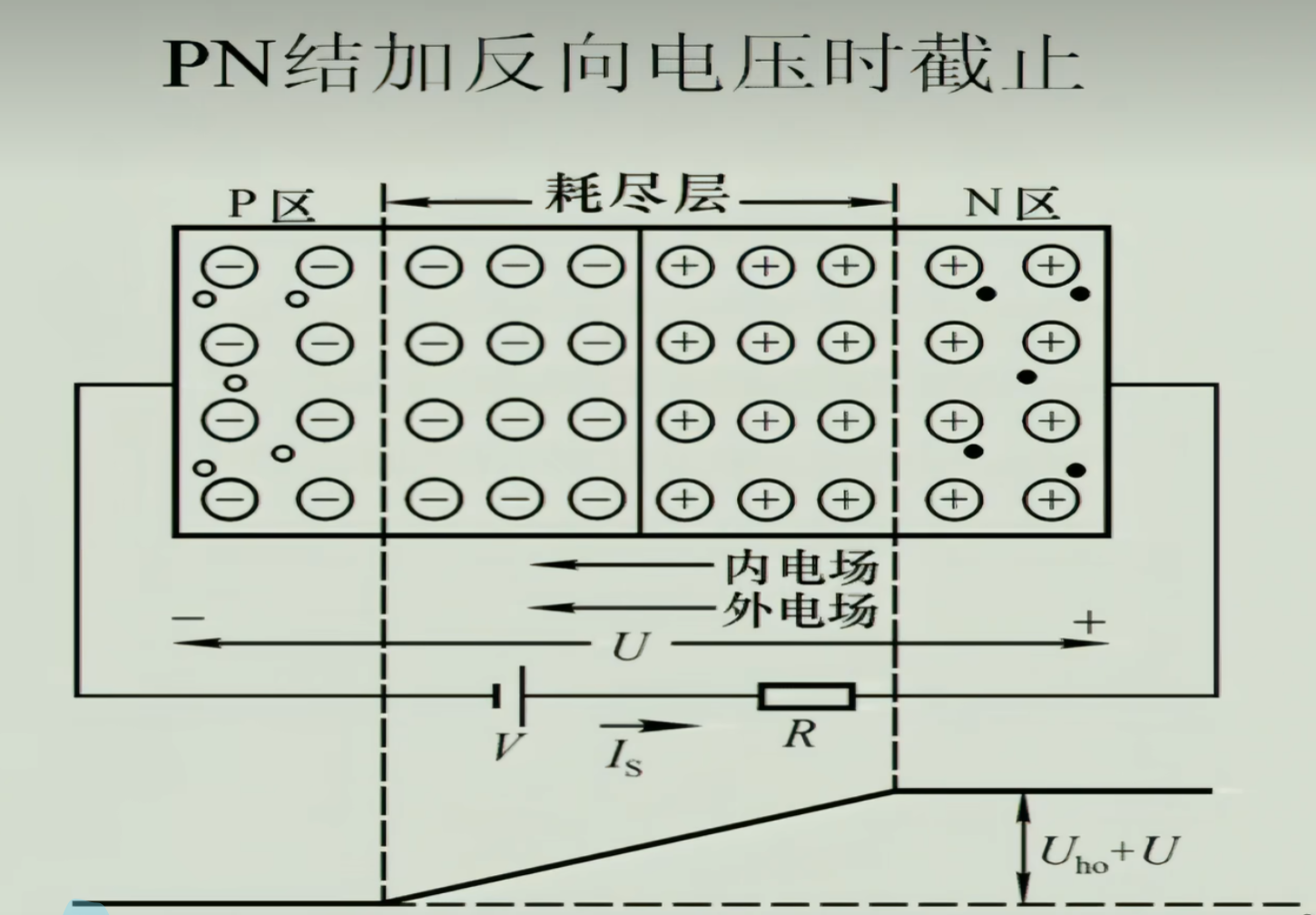
由于扩散运动(浓度差产生的,粒子从其浓度高的地方运动到浓度低的地方),N区的电子向P区,P区空穴向N区,中间形成空间电荷区:耗尽层/阻挡层/PN结
但是即使有这个PN结尽力形成堡垒阻止多子发生扩散运动,但是保不齐还有少量的多飞跃势垒,那么一旦有这种情况发生,慢慢地就会耗尽了。所以为什么还是能保持平衡呢,是因为少子的漂移运动。对多子来说PN结可能是一个势垒,但是对少子来说就是一个吸引物。少量的少子与少量的多子通过PN结,达到动态平衡。
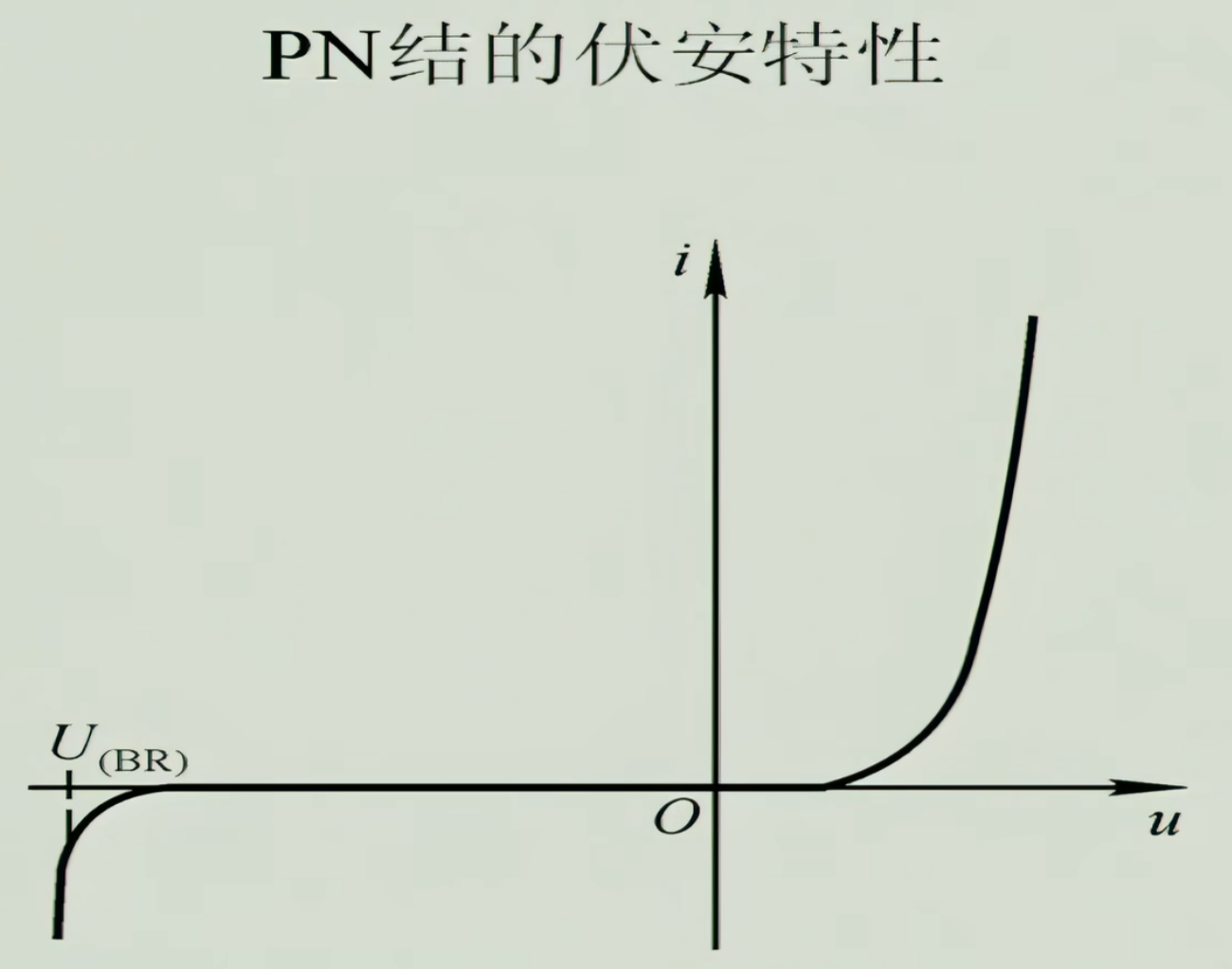
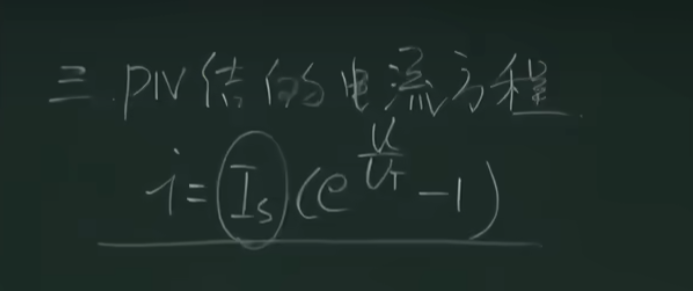
Is为反向饱和电流,UT为温度当量,室温下为26mV,U导通电压Ge管为0.2-0.3V,Si管为0.6-0.7V,因此后面的-1一般可以忽略。