[题目记录]AGC005E Sugigma: The Showdown

news/2025/1/10 16:35:22/文章来源:https://www.cnblogs.com/youlv/p/18664201

AGC005E Sugigma: The Showdown

题意

给出两棵树 , 点的编号相同 , 连边方式不同 .

初始 A 在树 $a$ 上的点 $x$ , B 在树 $b$ 上的点 $y$ , 两人轮流走 , 每人每轮可以向所在树上的一个相邻点走一步 , 也可以不走 . 当两个人所在的点编号相同时游戏结束 .

A 要最大化轮数 , B 要最小化轮数 , 问游戏轮数 . 如果可以进行无限轮 , 输出 $-1$ .

$n\le 2\times 10^5$ .

题解

首先发现可以把这个问题理解成 B 追逐 A . 然后发现 B 的决策可以说是相当 "被动" 的 . 首先 B 任何一轮都不会选择不动 , 因为如果 B 不动 , A 完全可以不动 , 相当于白白多了一轮 . 同理 , B 也不可能向着远离 A 的方向移动 , 否则 A 也可以不动让 B 至少亏一轮 .

因此 B 的决策是固定的 : 每次向 A 当前所在位置移动一格 .

此时只需研究 A 的决策即可 .

先研究一下题目中说的无限轮的情况 , 研究样例 4 , 发现这里是因为有一条 $a$ 边连接了 $b$ 树上的一条路径 , A 只需在 B 走到这条路径靠近自己的一半时换到另一边即可 , 而为了实现能 "遛" B , 这条路径的长度需要 $\ge 3$ .

因此 " 所有 $a$ 边对应的 $b$ 树上路径长度 $<3$ " 是轮数有限的 充分不必要条件 . 先考虑这个子问题 .

这提示我们从每一条 $a$ 边跨越的 $b$ 树上的路径来思考 . 考虑以 $y$ 为根 , 把 $b$ 视作有根树 , 把 $a$ 视作 $b$ 树上的一些连接边 .

这样变化后 , 因为每条 $a$ 边所能跨越的长度 $<3$ , 最多只能从根的一个儿子移动到另一个儿子 , 子树中的其他点都不能联通 , 而根的任何一个儿子都会在下一步被追上 . 因此 **A 无法在 B 当前所在节点的不同子树间移动 ** .

( A 此时只能向它自己的子树移动 )

这也侧面证明了上面的结论是正确的 , 因为 B 总是在缩小 A 可以移动的子树 , 直到 A 移动到一个叶子节点 , 游戏结束 .

而 A 要最大化轮数 , 只能移动到一个深度尽可能大的叶子 . 然而进入哪个叶子不完全由 A 决定 , 比如如下情况 :

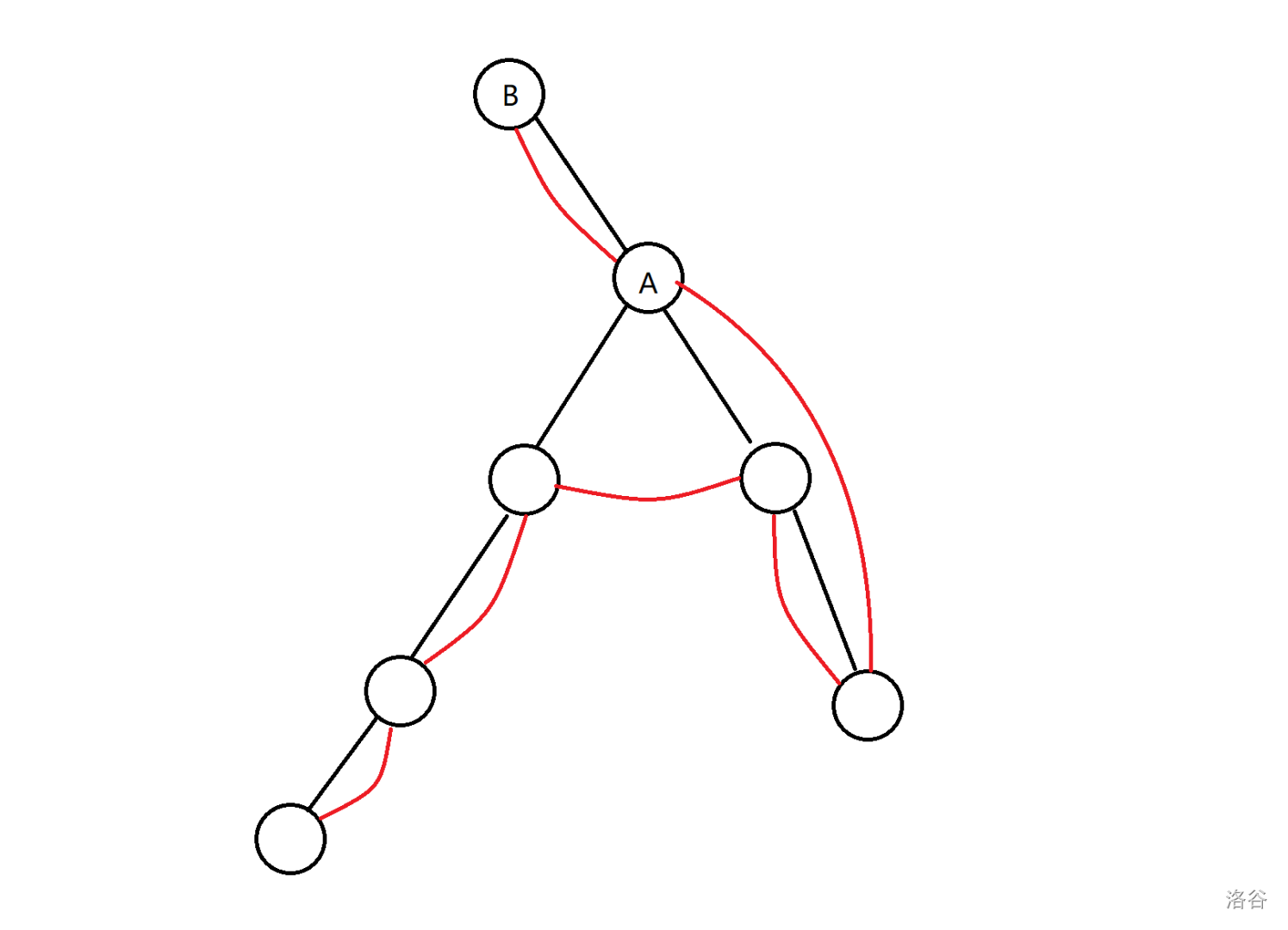
虽然左侧的链可以让轮数更多 , 但是 A 走到左儿子需要 $3$ 步 , 然而仅 $1$ 步之后左子树就会被向下走了一步的 B 封锁 . 究其原因 , A 走到右儿子需要两步 , 而 B 也需要两步 , 恰好在这一步结束 .

因此对于每个点设 $d_u$ 为在 $a$ 树 ( 以 $x$ 为根 ) 上的深度 , $d'_u$ 为在 $b$ 树上的深度 , 只有在 $d_u<d'_u $ 时 , 这个点才能在不在当前点被追上的情况下到达 , 而要到达 $u$ 需要保证从 $y$ 到 $u$ 的路径都满足 $d_x<d'_x$ .

通过这种方法 , 可以获得所有能够到达的点 , 取其中深度最大的点计算答案 .

然后考虑存在 $\ge 3$ 的边 . A 只要到达这种边的一个端点 , 就可以达到无限轮 , 到达这种边的端点相当于到达的终点 , 后面无需考虑 .

因此仍然只考虑 $<3$ 的边 , 用刚才的方法把所有能到达的点找出来 , 如果能到达 $\ge 3 $ 的边的端点就是无限轮 , 否则取深度最大的点计算答案 .

点击查看代码

#include<bits/stdc++.h>
#define file(x) freopen(#x ".in","r",stdin),freopen(#x ".out","w",stdout)
#define ll long long
#define INF 0x3f3f3f3f
#define INF64 1e18
using namespace std;constexpr int N=2e5+5;vector<int> e[N],g[N];
vector<pair<int,int> > ep;int n,x,y;int d[N],dep[N],dfn[N],rnk[N],tot,pos[N],fd[N*2][22],od,lg[N*2];void dfs1(int u,int fa){dfn[u]=++tot;rnk[tot]=u;fd[++od][0]=dfn[u];pos[u]=od;for(auto v:g[u]){if(v==fa) continue;dep[v]=dep[u]+1;dfs1(v,u);fd[++od][0]=dfn[u];}
}
void init(){for(int j=1;(1<<j)<=od;j++)for(int i=1;i+(1<<j)-1<=od;i++)fd[i][j]=min(fd[i][j-1],fd[i+(1<<(j-1))][j-1]);lg[1]=0;for(int i=2;i<=od;i++) lg[i]=lg[i/2]+1;
}
int LCA(int x,int y){x=pos[x],y=pos[y];if(x>y) swap(x,y);int t=lg[y-x+1];return rnk[min(fd[x][t],fd[y-(1<<t)+1][t])];
}int dist(int x,int y){return dep[x]+dep[y]-2*dep[LCA(x,y)];
}bitset<N> vis;int res,ok;void dfs2(int u,int fa){if(d[u]>=dep[u]) return;if(vis[u]) ok=1;else res=max(res,dep[u]);for(auto v:e[u]){if(v==fa) continue;d[v]=d[u]+1;dfs2(v,u);}
}int main(){ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);cin>>n>>x>>y;for(int i=1;i<n;i++){int u,v;cin>>u>>v;ep.push_back({u,v});}for(int i=1;i<n;i++){int u,v;cin>>u>>v;g[u].push_back(v);g[v].push_back(u);}dfs1(y,y);init();for(auto [u,v]:ep){if(dist(u,v)>2) vis[u]=vis[v]=1;e[u].push_back(v);e[v].push_back(u);}dfs2(x,x);if(ok) cout<<-1;else cout<<2*(res);
}