- 伊基的故事 I - 道路重建
- 网络流题,在跑完 dinic 后,在残量网络上找 \(f(u,v)=0\),满足存在 \(s\rightarrow u,v \rightarrow t\) 的边。代码。
- [USACO05FEB] Secret Milking Machine G
-
网络流题,明显二分答案。网络可以直接建反向边,因为流两次相当于没流。
code
const int N = 205; const int M = 8e4 + 5; const int inf = 2147483647;int head[N], ver[M], _edge[M], Next[M], tot = 1; int n, p, T, d[N], now[N], s, t; queue<int> que; int edge[M];void add(int u, int v, int w) {ver[++tot] = v, _edge[tot] = w;Next[tot] = head[u], head[u] = tot; }bool bfs() {memset(d, 0, sizeof d);while (que.size()) que.pop();d[s] = 1, que.push(s), now[s] = head[s];while (que.size()) {int u = que.front(); que.pop();for (int i = head[u]; i; i = Next[i]) {int v = ver[i], w = edge[i];if (w && !d[v]) {d[v] = d[u] + 1;now[v] = head[v];if (v == t) return 1;que.push(v);}}}return 0; }int dfs(int u, int f) {if (u == t || !f) return f;int res = 0;for (int &i = now[u]; i; i = Next[i]) {if (edge[i] && d[ver[i]] == d[u] + 1) {int k = dfs(ver[i], min(f, edge[i]));if (!k) d[ver[i]] = 0;edge[i] -= k, edge[i ^ 1] += k;f -= k, res += k;if (f <= 0) break;}}return res; }int dinic() {int res = 0, f;while (bfs()) while (f = dfs(s, inf)) res += f;return res; }bool check(int val) {LF(i, 2, tot) edge[i] = (_edge[i] <= val ? 1 : 0);if (dinic() >= T) return 1;return 0; }int main() {cin >> n >> p >> T;s = 1, t = n;LF(i, 1, p) {int u, v, w; cin >> u >> v >> w;add(u, v, w);add(v, u, w);}int l = 1, r = 1e6;while (l < r) {int mid = (l + r) >> 1;if (check(mid)) r = mid;else l = mid + 1;}cout << l;return 0; }
-
泛做题记录
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.hqwc.cn/news/867342.html
如若内容造成侵权/违法违规/事实不符,请联系编程知识网进行投诉反馈email:809451989@qq.com,一经查实,立即删除!相关文章
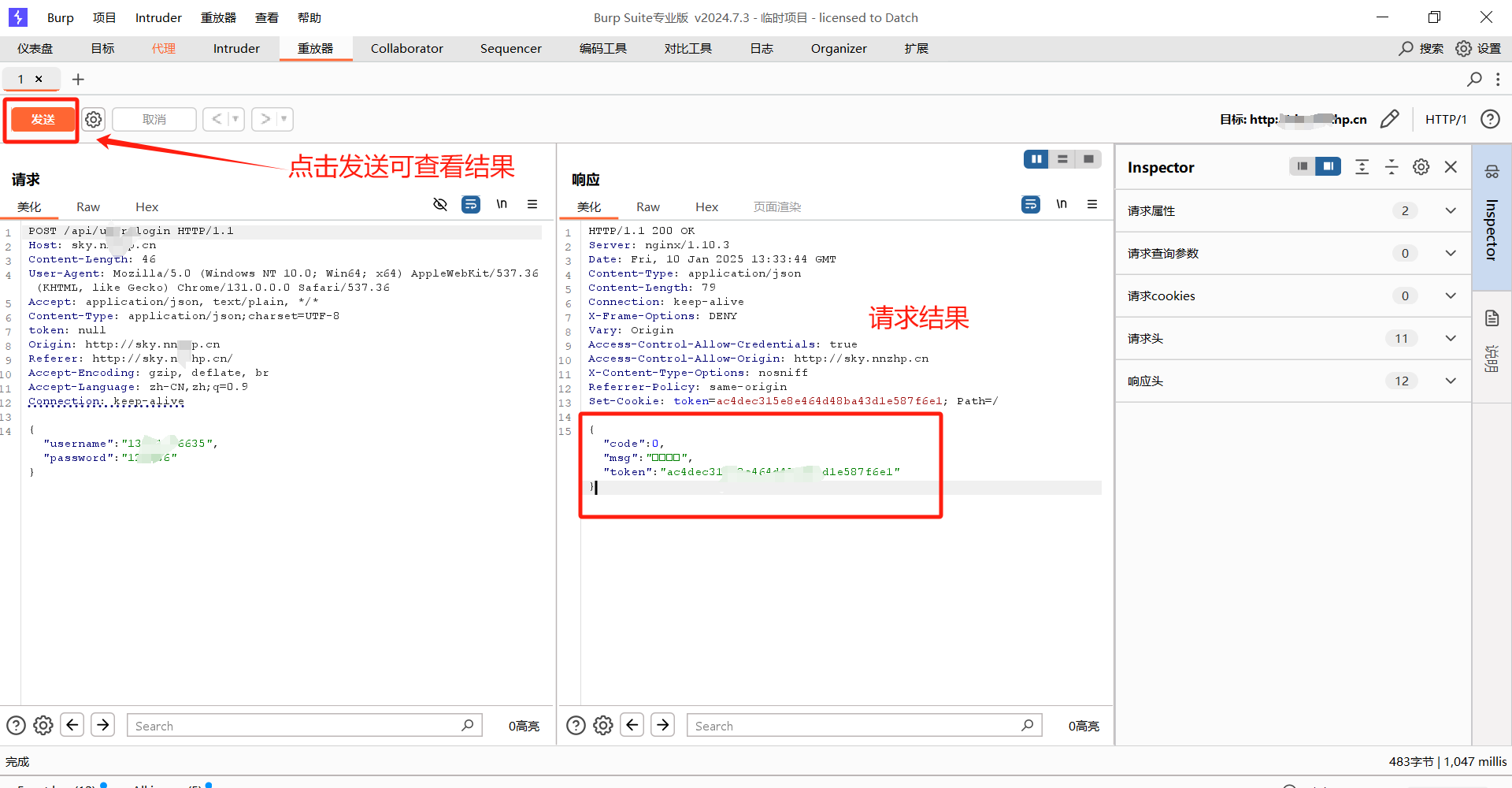
BurpSuite实操之重发器功能使用
手动操作来触发单独的HTTP请求,并进行应用程序响应的工具,此功能用于根据不同的情况修改和发送相后的请求并分析,通过调整Request的参数,不断尝试,通过Response查看状态,从而节省在浏览器中操作的时间。
在渗透测试过程中,我们经常使用Repeater进行请求与响应的消息验证…
G1原理—3.G1是如何提升垃圾回收效率
大纲
1.G1为了提升GC的效率设计了哪些核心机制
2.G1中的记忆集是什么
3.G1中的位图和卡表
4.记忆集和卡表有什么关系
5.RSet记忆集是怎么更新的
6.DCQ机制的底层原理是怎样的
7.DCQS机制及GC线程对DCQ的处理提升G1垃圾回收器GC效率的黑科技
G1设计了一套TLAB机制 + 快速分配机制…
1.10日学习笔记之C++的类
类其实就是一种数据类型,和结构相似。类的成员包括两类,属性(成员变量)和行为(成员函数)。
成员函数定义的两种方法(可能有多种,觉得这两种比较常用)
1、将类的成员函数定义在类体内,如
class CPerson
{public: short age;short getage(){return age;}};2、将类的成…
着火智能监测识别摄像机
着火智能监测识别摄像机利用了先进的图像处理技术和人工智能算法,能够快速、准确地检测环境中的着火点,从而及时采取必要的安全措施。其工作原理如下:首先,摄像机配备高清摄像头,能够实时捕捉并传输环境图像。这些图像通过内置的处理单元,进行高效处理和分析。其次,利用…
BurpSuite实操之测试器功能
对web应用程序进行自动化攻击。此功能有多种用途,如漏洞利用、模糊测试、进行暴力pojie等1、目标设置代理发送过来请求的目标主机及端口信息。
输入要攻击的目标及端口2、位置设置在这个模块可以设置攻击的参数,及攻击使用的类型(1)Sniper-狙击手(2)Battering ram-破城锤…
采沙船智能监测识别摄像机
采沙船智能监测识别摄像机还支持数据记录和分析功能,可以生成详尽的非法采沙统计报告和趋势分析,为河流管理决策提供科学依据。管理部门可以通过监控系统的数据分析,制定精准的禁采政策和优化河流资源管理,有效保护水域生态环境,防止非法采砂对生态系统的破坏。在实际应用…
C api简单查询需要的几步
C api查询简单需要的几步
1.准备sql语句
2.绑定变量
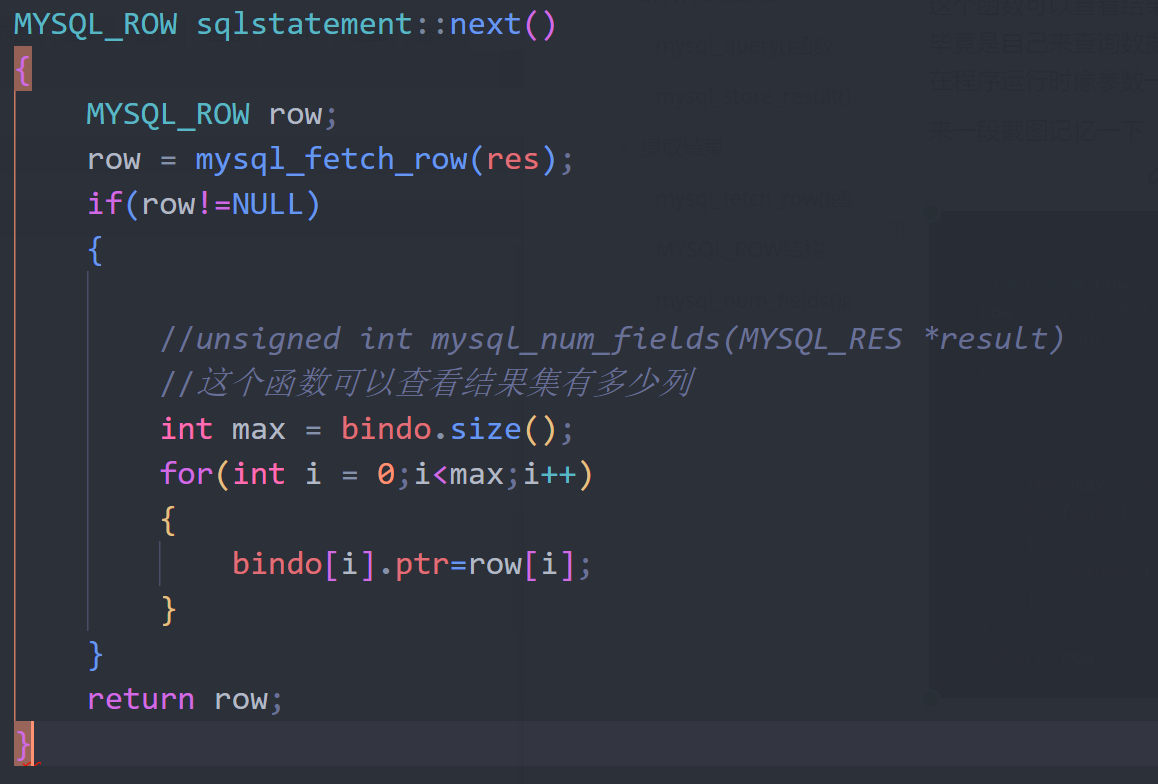
通过sqlstatement类bindout方法将查询出来的值与存储他们的变量绑定。 这里绑定是为了以后从结果集中提取一行时只需要一行就可以完成将提取出 来的变量赋值。
3.执行execute
在这一步将sql语句执行。在这里有几个重点
mysql…
22. MDI窗口设计
一、什么是MDI窗口MDI 窗口(Multiple-Document Interface),又称多文档界面,它主要用于同时显示多个文档,每个文档显示在各自的窗口中。MDI 窗口中通常包含子菜单和窗口菜单,用于在窗口或文档之间进行切换。用 QMainWindow 建立的主界面,通常会同时建立或打开多个相互独立…
详解:订单履约系统规划
大家好,我是汤师爷~
什么是订单履约系统?
订单履约是从消费者下单支付到收到商品的全流程管理过程,包括订单接收、订单派单、库存分配、仓储管理和物流配送等环节,核心目标是确保商品准时、准确地送达消费者手中。
通过订单履约系统,消费者可以实时了解商品的物流状态和预…
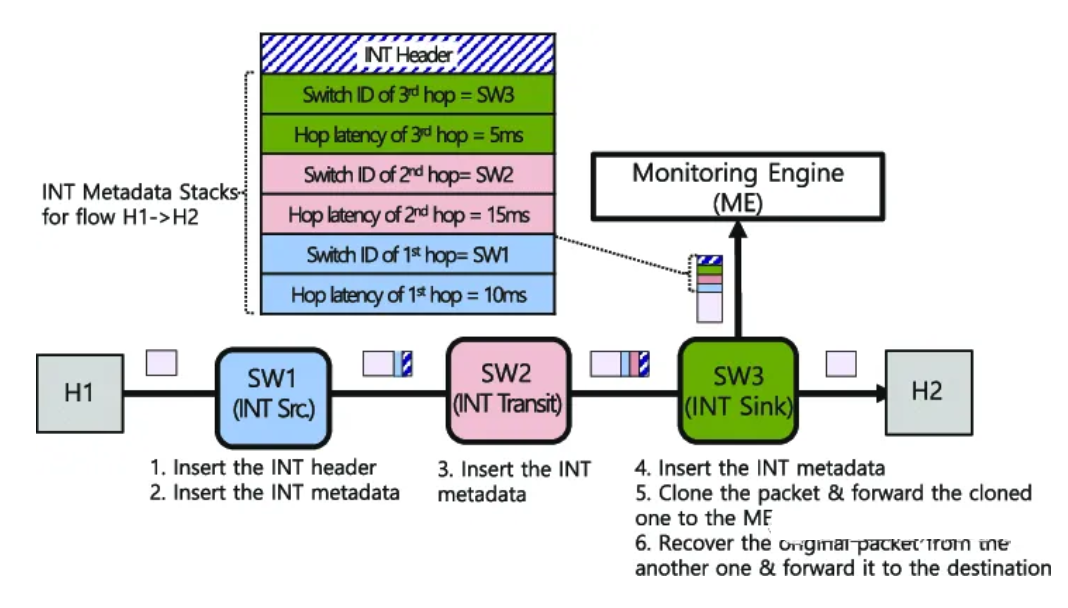
In‐band Network Telemetry
#卫星 #遥测技术 #INT
一、INT是什么?
INT,In‐band Network Telemetry ,带内网络遥监测。telemetry,英文原意是遥测技术。从其英文名称可以了解如下:
a.In-band,说明监测指令及数据均在带内传输
b.telemetry ,说明是长距离,远程获取网络数据的方法。
想象一下卫星在…