P1792 [国家集训队] 种树

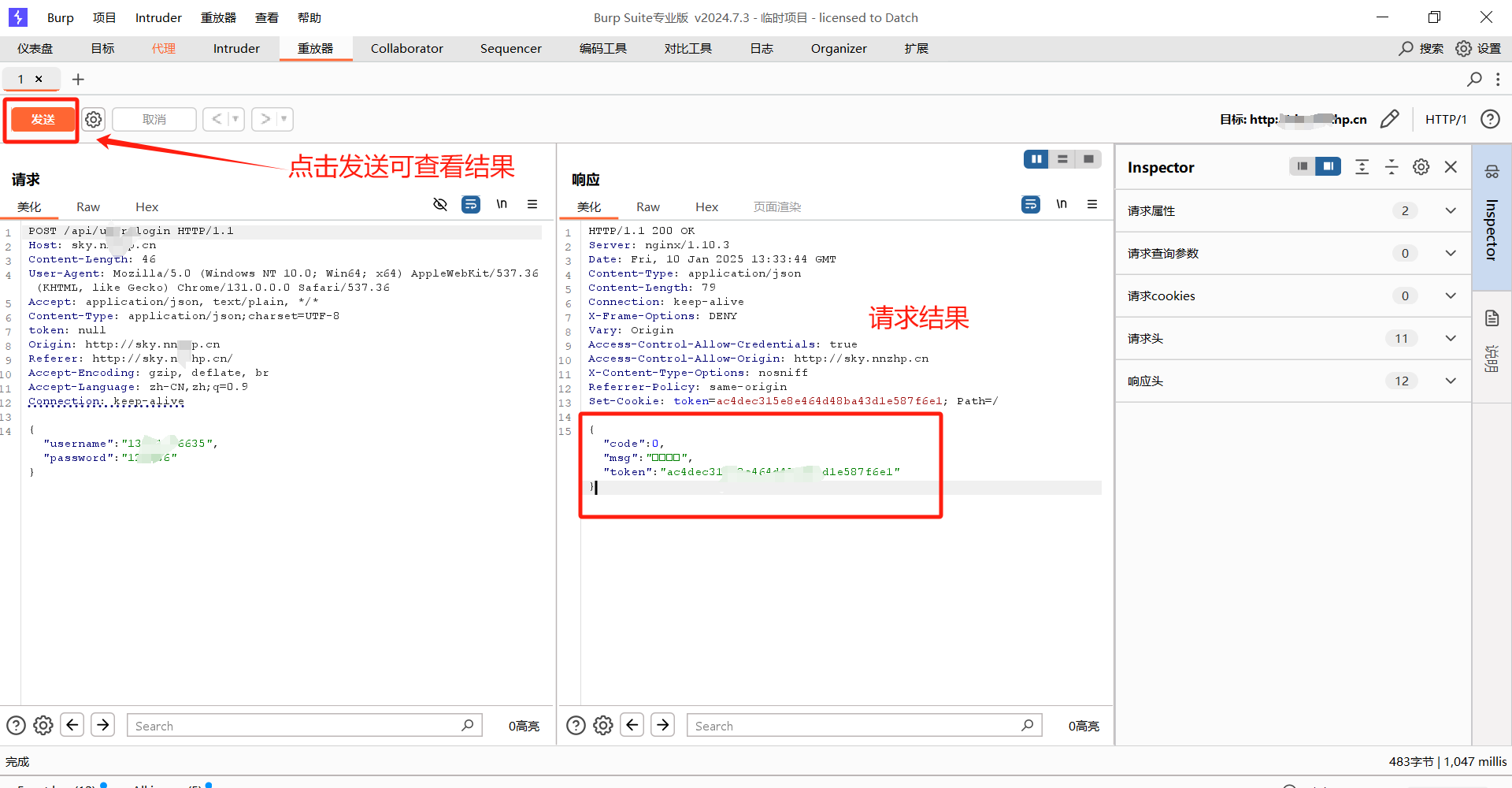
题意：给一个长度为n的环形数组，你要选m个数，满足没有任意两个数的位置相邻，求总和最大。

一开始没仔细看数据范围写了个dp暴力，想着枚举第1个点选还是不选两次dp取最大值。(属于痴心妄想）
后面自己也是看的题解。我们先贪心选最大的，那么它两边就不可以选了，但有可能选两边比选这个更好，那么我们就选两边，这样怎么处理?我们先选了第i个，加上了\(a_i\)，那么如果我们不选这个而选旁边两个，是不是要加上\(a_{i-1}\) 和 \(a_{i + 1}\)，如何要减掉\(a_i\)。那么我们用一个新点来替代当前点，它的值为\(a_{i-1}\) + \(a_{i + 1}\) - \(a_i\)。
因为不能相邻，所以m最多\(\lfloor n \rfloor\)个。
用优先队列模拟即可。

点击查看代码

void solve() {int n, m;std::cin >> n >> m;if (m > n / 2) {std::cout << "Error!\n";return;}std::priority_queue<std::pair<int, int> > heap;std::vector<int> l(n), r(n), val(n);for (int i = 0; i < n; ++ i) {std::cin >> val[i];l[i] = i - 1;r[i] = i + 1;	heap.push({val[i], i});}l[0] = n - 1; r[n - 1] = 0;auto del = [&](int p) -> void {l[r[p]] = l[p];r[l[p]] = r[p];};int ans = 0;std::vector<int> vis(n);while (m -- ) {while (vis[heap.top().second]) {heap.pop();}auto [v, id] = heap.top(); heap.pop();vis[l[id]] = vis[r[id]] = 1;ans += v;val[id] = val[l[id]] + val[r[id]] - v;heap.push({val[id], id});del(l[id]); del(r[id]);}std::cout << ans << "\n";
}