群
定义
半群的定义:设S是一个具有结合法的非空集合.如果S中有一个元素e;使得对S中所有元素a,都有 ea=ae=a.
单位元的定义:
性质:设 S是一个有单位元的半群, 则对 S 中的任意可逆元 a, 其逆元 a' 是唯的
群的定义:
子群
定义:
同态和同构
定义:
单射、满射、双射:
单射确保不同的输入产生不同的输出。换句话说,函数不会将两个不同的元素映射到同一个元素。
满射确保函数的输出覆盖了整个目标集合B。换句话说,所有可能的输出都有对应的输入。
如果既是单射又是满射,那么就称为双射
记为: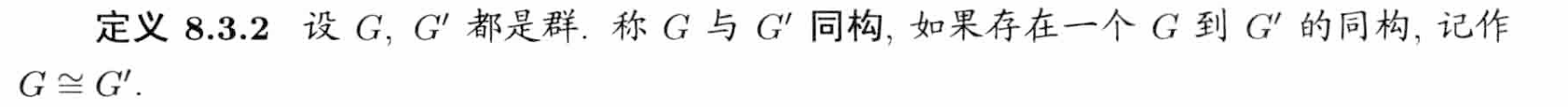
同态五大定理:

解释:1、2不必多说,3要满足单同态即不同输入对应不同输出,那必然只可能有一个元素;4理所当然;5:G’的子群H‘通过f^-1会得到G的子群
出题
1 证明群(四大公理)
2 判断同构
坑点:
(ab)-1=b-1 a^-1
陪集
陪集和代表元的定义:
定理:
(元素的)阶

例如乘群中
1的阶是1 --》 1=1
-1的阶是2 --》(-1)*(-1)=1
其他数为无穷大,因为m为正整数
变换群
即证明一个变换如x-》f(x)是不是一个群
例题:贴个链接
30min左右
置换
有限集上的一一变换
变换方式:(A,B,C,。。。,D)=》A换成B,B换成C,。。。,D换成A。
例题: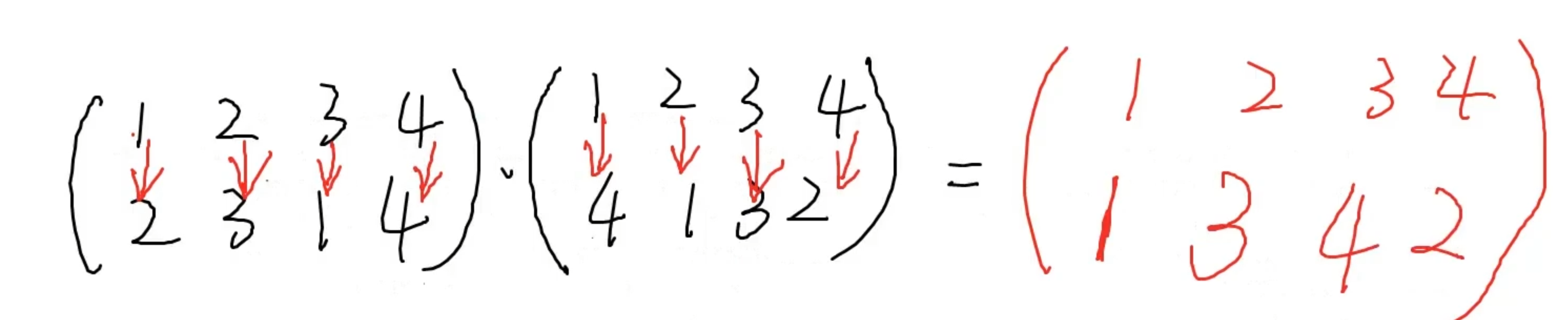
从左置右 与 从右置左 虽然结果不一样,但是对意义没什么影响。