【学习笔记】斜率优化 dp

Foreword

斜率优化，顾名思义就是用一次函数的单调性来优化 dp，具体表现为利用单调性找到最优决策点从而优化掉需要枚举的决策点。

给斜率优化 dp 总结一个模板：

\[dp_{i} = \min\{dp_{j} + calc (i,j)\} \]

或者：

\[dp_{i} = \max\{dp_{j} + calc (i,j)\} \]

其中 \(j\) 为我们所枚举的决策点，从 \(j\) 转移到当前决策点 \(i\)，\(calc\) 函数表示需要最小 / 最大化的答案。

Type

斜率优化分类可以根据横坐标和斜率的单调性分成以下：

1. 斜率单调，横坐标单调。

2. 斜率不单调或横坐标不单调。

3. 都【数据删除】的不单调。

这三种都可以用李超线段树，cdq，平衡树维护，对于第二种可以单调队列 / 单调栈和二分解决，以上都是 \(O(n \log n)\) 的复杂度，但是第一种可以只用单调队列做到 \(O(n)\)。

李超线段树

这里简单介绍一下。

李超线段树可以看做是线段树的一个变种，其中一个节点代表横坐标的一个区间，支持动态插入线段，然后就可以维护区间上的优势线段，具体过程如下：

1. 插入线段，一般是动态插入（即动态开点）。

2. 判断新加入的线段是否全覆盖原线段。

3. 如果是就直接将树上当前节点的线段替换成新加入线段，反之，判断两条线段在 \(mid\) 处的 \(y\) 值大小，若交点在 \(mid\) 左侧，故右侧谁更优是确定的，递归求解左侧，交点在 \(mid\) 右侧同理。

Ex.1 P10979 任务安排 2

它还有一个弱化版 P2356，和一个强化版 P5785。

Solution

首先考虑 \(O(n^2)\) 的暴力 dp，我们记 \(dp_i\) 表示已经处理完前 \(i\) 个任务的最小花费，枚举前 \(i\) 个中分批于 \(j\) 位置，对于处理任务的花费，我们可以记 \(sumt_i,sumf_i\) 两个前缀和，花费即为 \(sumt_i \times (sumf_i - sumf_j)\)，对于启动机器的时间，显然它对后面 \([j + 1.n]\) 需要处理的任务会产生影响，故一同考虑，得到转移式子：

\[dp_{i} = \min_{j=0}^{i-1}{dp_{j} + sumt_i \times (sumf_i - sumf_j) + S \times (sumf_n - sumf_j)} \]

显然这是 \(O(n^2)\) 的，可以通过弱化版，考虑优化。

我们来拆掉这个柿子：

\[dp_{i} = \min_{j=0}^{i-1}{dp_{j} + sumt_i \times sumf_i -sumt_i \times sumf_j + S \times sumf_n - S \times sumf_j} \]

暂时拆掉 \(\min\) 并且移个项：

\[dp_j = sumf_j \times (sumt_i + S) + dp_i - sumt_i \times sumf_i - S \times sumf_n \]

显然的，在 \(i\) 一定的情况下，\(dp_i - sumt_i \times sumf_i - S \times sumf_n\) 为定值，令 \(y = dp_j,x = summf_j\)：

\[y = x \times (sumt_i + S) + dp_i - sumt_i \times sumf_i - S \times sumf_n \]

显然的关于 \(x\) 的一次函数，斜率为 \(k = (sumt_i + S)\)，截距为 \(b = dp_i - sumt_i \times sumf_i - S \times sumf_n\)。

所以说建立平面直角坐标系，决策点集中每个点为 \((sumf_j,dp_j)\)，我们现在就将题意转化成了对于一条直线 \(y' = kx + b'\)，其中 \(b' \in (-\infty,\infty)\)，使得它与决策点集中的点相交后 \(b'\) 计算出来最小。

如下图：

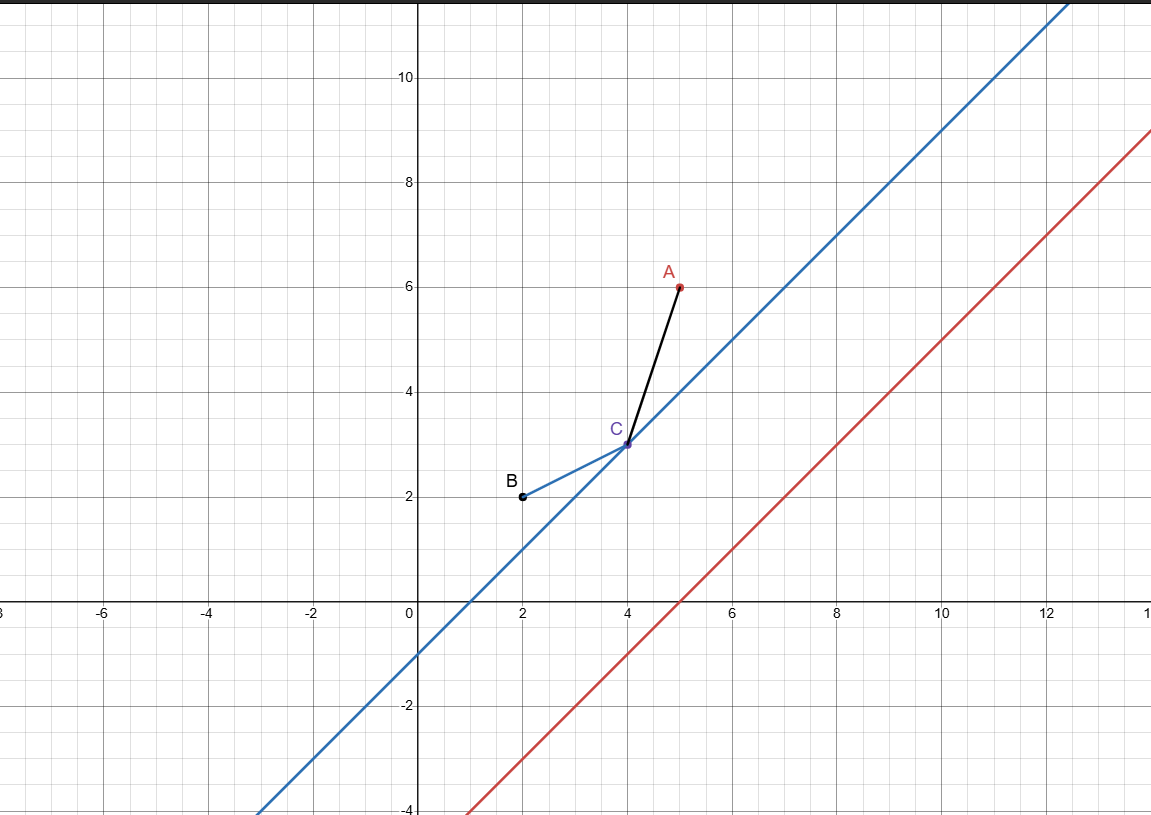
红色图像为 \(y'\)，蓝色图像为它与 \(C\) 所交。

显然 \(C\) 点为最优决策点，且所有最优决策点定位于下凸壳。

考虑如何维护，对于直线 \(l_{p_ip_{i-1}}\) 和直线 \(l_{p_ip_{i+1}}\)，在满足 \(k_{l_{p_ip_{i-1}}} < k <k_{l_{p_ip_{i+1}}}\) 时点 \(p_i\) 为最优决策点，故选用具有单调性的容器（此处使用单调队列）进行操作，每次二分找到满足该条件的点，然后插入当前决策点 \(i\)，检查 \(i\) 是否与上一个点构成下凸壳，否则就踢掉队尾直到符合下凸壳，即为保证新加入的直线的斜率大于队尾直线的斜率，每次插入新决策点前 dp 转移即可，复杂度 \(O(n \log n)\)。

但是其实有更优做法，所以该题为 P5785 弱化版。

由于本题 \(t_i,c_i\) 满足为正整数，斜率和截距单增，因此下凸壳加入新决策点一定是不断向右加入，只需要在转移前在单调队列中去除无用策略，因为凸包最左侧的点一定是最优的，所以对于当前的 \(k\)，判断队头直线的斜率，不断踢出队头直到找到第一个大于 \(k\) 的队头作为最优决策点转移，这个操作均摊 \(O(1)\)，故总复杂度 \(O(n)\)。

Code

\(O(n \log n)\) 做法。

#include <bits/stdc++.h>
#define int long longusing namespace std;
inline int read() {int res = 0, f = 1;char ch = getchar();while (!isdigit (ch)) f = ch == '-' ? -1 : 1, ch = getchar();while (isdigit (ch)) res = (res << 1) + (res << 3) + (ch ^ 48), ch = getchar();return res * f;
}
const int MAXN = 3e5 + 10;
int n, S, dp[MAXN], t[MAXN], f[MAXN], preSumt[MAXN], preSumf[MAXN], q[MAXN], head, tail;signed main() {n = read(), S = read();for (int i = 1; i <= n; i ++)t[i] = read(), f[i] = read();for (int i = 1; i <= n; i ++) {preSumt[i] = preSumt[i - 1] + t[i];preSumf[i] = preSumf[i - 1] + f[i];}for (int i = 1; i <= n; i ++) {int l = head, r = tail, mid = 0;while (l < r) {mid = l + r >> 1;if (dp[q[mid + 1]] - dp[q[mid]] >= (preSumf[q[mid + 1]] - preSumf[q[mid]]) * (preSumt[i] + S)) r = mid;else l = mid + 1;}dp[i] = dp[q[l]] - (S + preSumt[i]) * preSumf[q[l]] + preSumt[i] * preSumf[i] + S * preSumf[n];while (head < tail && (__int128_t)(dp[q[tail]] - dp[q[tail - 1]]) * (preSumf[i] - preSumf[q[tail]]) >= (__int128_t)(dp[i] - dp[q[tail]]) * (preSumf[q[tail]] - preSumf[q[tail - 1]])) tail --;q[++ tail] = i;}printf ("%lld\n", dp[n]);return 0;
}

\(O(n)\) 做法。

#include <bits/stdc++.h>
#define int long longusing namespace std;
inline int read() {int res = 0, f = 1;char ch = getchar();while (!isdigit (ch)) f = ch == '-' ? -1 : 1, ch = getchar();while (isdigit (ch)) res = (res << 1) + (res << 3) + (ch ^ 48), ch = getchar();return res * f;
}
const int MAXN = 3e5 + 10;
int n, S, dp[MAXN], t[MAXN], f[MAXN], preSumt[MAXN], preSumf[MAXN], q[MAXN], head, tail;signed main() {n = read(), S = read();for (int i = 1; i <= n; i ++)t[i] = read(), f[i] = read();for (int i = 1; i <= n; i ++) {preSumt[i] = preSumt[i - 1] + t[i];preSumf[i] = preSumf[i - 1] + f[i];}for (int i = 1; i <= n; i ++) {while (head < tail && (__int128_t)(dp[q[head + 1]] - dp[q[head]]) <= (__int128_t)(preSumf[q[head + 1]] - preSumf[q[head]]) * (preSumt[i] + S)) head ++;dp[i] = dp[q[head]] - (S + preSumt[i]) * preSumf[q[head]] + preSumt[i] * preSumf[i] + S * preSumf[n];while (head < tail && (__int128_t)(dp[q[tail]] - dp[q[tail - 1]]) * (preSumf[i] - preSumf[q[tail]]) >= (__int128_t)(dp[i] - dp[q[tail]]) * (preSumf[q[tail]] - preSumf[q[tail - 1]])) tail --;q[++ tail] = i;}printf ("%lld\n", dp[n]);return 0;
}

Warning

计算斜率可以使用交叉相乘规避掉精度问题，但是有可能暴 longlong 需要 int128。

Ex.2 P4655 [CEOI2017] Building Bridges

首先还是思考 \(O(n^2)\) 柿子。

记 \(dp_{i}\) 表示前 \(i\) 根柱子连接的最小代价，记 \(sumw_i\) 为 \(w_i\) 前缀和，得到转移：

\[dp_i = \min_{j=0}^{i-1}\{dp_j + (h_i - h_j)^2 + sumw_{i-1} - sumw_j\} \]

拆柿子：

\[dp_i = dp_j + h_i^2 - 2h_ih_j + h_j^2 + sumw_{i-1} - sumw_j \\ \ \\ \Downarrow \\ \ \\ k_i = -2 \times h_i \\ b_j = dp_j + h_j^2 - sumw_j \\ y_i = dp_i - h_i^2 - sumw_{i-1} \\ x_j = h_j \\ dp_i = h_i^2 + sumw_{i-1} + \min_{j=0}^{i-1}\{k_ix_j + b_j\} \]

\(\min\) 当中的可以看做维护区间上的最低线段，可以用李超线段树维护，复杂度 \(O(n \log n)\)。

#include <bits/stdc++.h>
#define int long longusing namespace std;
inline int read() {int res = 0, f = 1;char ch = getchar();while (!isdigit (ch)) f = ch == '-' ? -1 : 1, ch = getchar();while (isdigit (ch)) res = (res << 1) + (res << 3) + (ch ^ 48), ch = getchar();return res * f;
}
const int MAXN = 1e6 + 10, inf = LLONG_MAX;
int n, h[MAXN], w[MAXN], sumw[MAXN], dp[MAXN], ind, rt;
inline int Getx (int p) { return h[p]; }
inline int Getb (int p) { return dp[p] + h[p] * h[p] - sumw[p]; }
inline int Getk (int p) { return -2 * h[p]; }
struct line {int k, b;line (int k = 0, int b = 0):k(k), b(b){};int Getfx (int x) { return k * x + b; }
};
struct Ayaka {int lson, rson;line ln;bool isCover;
}seg[MAXN << 2];void Modify (int &rt, line lnx, int l, int r) {if (!rt) rt = ++ ind;int lpos = seg[rt].ln.Getfx (l), rpos = seg[rt].ln.Getfx (r);int tmpLpos = lnx.Getfx (l), tmpRpos = lnx.Getfx (r);if (!seg[rt].isCover)seg[rt].isCover = true, seg[rt].ln = lnx;else if (tmpLpos <= lpos && tmpRpos <= rpos) seg[rt].ln = lnx; /* 原线段完全在新线段之下 */else if (tmpLpos <= lpos || tmpRpos <= rpos) {int mid = l + r >> 1;if (seg[rt].ln.Getfx (mid) > lnx.Getfx (mid)) swap (seg[rt].ln, lnx); /* 如果新线段在 mid 处比原线段小则交换 */if (seg[rt].ln.Getfx (l) > lnx.Getfx (l)) Modify (seg[rt].lson, lnx, l, mid); /* 右侧一定更优递归左侧 */else Modify (seg[rt].rson, lnx, mid + 1, r); /* 左侧一定更优递归右侧 */}return;
}int query (int pos, int rt, int l, int r) {if (!rt) return inf;int tmpVal = seg[rt].ln.Getfx (pos);if (l == r) return tmpVal;int mid = l + r >> 1;if (pos <= mid)tmpVal = min (tmpVal, query (pos, seg[rt].lson, l, mid));elsetmpVal = min (tmpVal, query (pos, seg[rt].rson, mid + 1, r));return tmpVal;
}signed main() {n = read();for (int i = 1; i <= n; i ++) h[i] = read();for (int i = 1; i <= n; i ++)w[i] = read(), sumw[i] = sumw[i - 1] + w[i];Modify (rt, line (0, inf), 1, 1e6);Modify (rt, line (Getk (1), Getb (1)), 1, 1e6);for (int i = 2; i <= n; i ++) {dp[i] = query (Getx (i), 1, 1, 1e6) + h[i] * h[i] + sumw[i - 1];Modify (rt, line (Getk (i), Getb (i)), 1, 1e6);}printf ("%lld\n", dp[n]);return 0;
}

Ex.3 P4072 [SDOI2016] 征途

这是一道需要考虑两个维度的问题，还是先考虑暴力 \(O(n^3)\) 的 dp 方程。

记 \(dp_{i,j}\) 表示前 \(j\) 天走 \(i\) 段路的最小答案。

首先，我们需要知道答案式子，记总路程为 \(S\)，记 \(d_i\) 为每段路的长度，答案：

\[\begin{aligned} Ans &= m^2 \times \frac{\sum\limits_{i=1}^{m}{(di - \frac{S}{m})^2}}{m} \\ &= \frac{\sum\limits_{i=1}^{m}{(m \times d_i - m \times S)^2}}{m} \\ &= \frac{\sum\limits_{i=1}^{m}{(m^2d_i^2 - 2Smd_i + mS^2)}}{m} \\ &= m \cdot (\sum\limits_{i=1}^{m}{d_i})^2 - S^2 \end{aligned} \]

只需要维护 \((\sum\limits_{i=1}^{m}{d_i})^2\) 的最小值就行，所以 dp 方程：

\[dp_{i,j} = \min^{i-1}_{k=0}\{dp_{k,j-1} + (sumd_i - sumd_k)^2\} \]

设决策点 \(k\) 优于 \(l\)：

\[dp_{k,j-1} + sumd_i^2 - 2sumd_isumd_k + sumd_k^2 < dp_{l,j-1} + sumd_i^2 - 2sumd_isumd_l + sumd_l^2 \\ \ \\ \downarrow \\ \ \\ (dp_{k,j-1} + sumd_k^2) - (dp_{l,.j-1} + sumd_l^2) < 2sumd_i \times (sumd_k - sumd_l) \\ \ \\ \downarrow \\ \ \\ \frac{(dp_{k,j-1} + sumd_k^2) - (dp_{l,.j-1} + sumd_l^2)}{(sumd_k - sumd_l)} < 2sumd_i \]

然后就斜率优化，分子看做 \(y\)，分母看做 \(x\)，注意每次从 \(j - 1\) 转移。

Summary

斜率优化题单