AVL树的插入

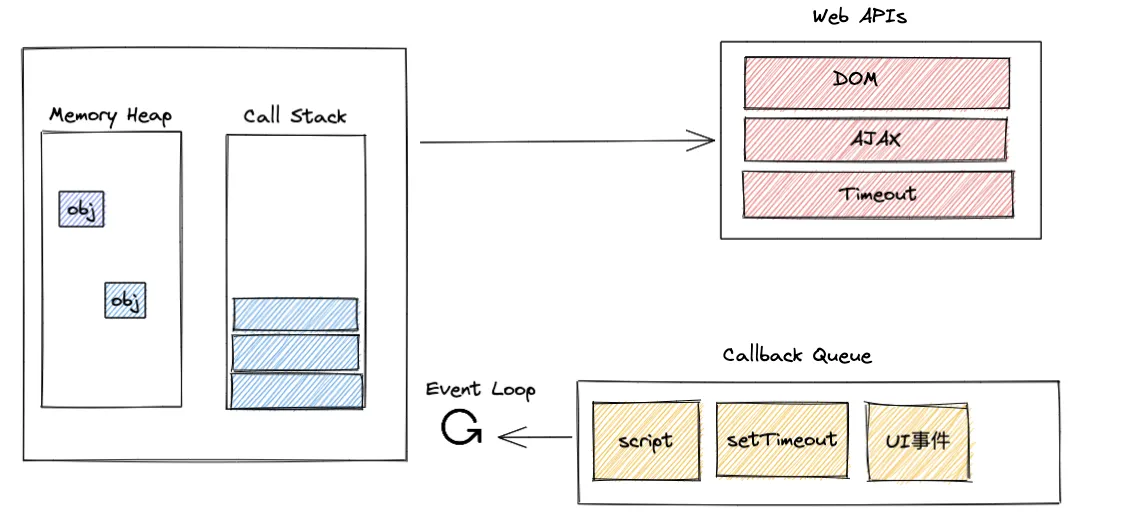
关于AVL树的插入，其实是一个比较复杂的问题，主要是在于他对于“旋转”这一概念，对于这一概念其实我感觉很多博主讲的都不是很明白，包括CHATGPT，也试了，但是也没有比较清楚的解释，他们主要集中在一种比较简单的情况，即没有任何子树的情况，如下所示

​

​
对于这种最基本的平衡维护，确实不是一件困难的事情，这个可以作为一种技巧，来帮助我们快速的来去得到答案。所以在这里，我会先从最基本的情况来去讲解这里是怎么个操作的流程，这里会不用“旋转”这一概念来解释平衡的维护，而是一种更加简单易懂的方式来讲解。

(注  本次的博客会在发布之后补充上代码，现在不会添加代码，只是会提供相关的概念)

其实个人觉得看到不错的是这个，推荐一下便于大家学习https://www.hello-algo.com/chapter_tree/avl_tree/#2_1

OK。可恶的作者终于把他的废话说完了，现在开始要说内容了。

首先是对于这里的基本情况。

如下所示

可以看到是有四种情况，这里即是插入节点后失衡的四种情况。对于这四种情况，我们可以对他们做一个分类，分为直线型和弯线型。

为什么叫直线型和弯线型，其实在这里是非常明显的(这里当然很明显，但是对于实际的节点插入来说就不是特别明显了)，我们将插入的节点向上回溯，然后一直到第一个失衡点，这样子来看，到达第一个失衡点之后，向下往插入点的方向标记三个单位，这个三个点就是接下来要主要操作的三个点了。

如下所示，

可以看到如上面的图片所示，可以知道，他为什么叫直线型和弯线型。那么接下来，就是如何对他们做操作呢，其实也是很简单的。

对于直线型，我们要做的就是把他掰弯，为了方便起见，我们将这三个点由上到下分别叫做爷爷，父亲，儿子。那么要做的是把爷爷弯折至和儿子一个高度，让后再将父亲给连接上。

对于弯线型，则是不一样，我们要先将它弄直，然后再像直线型一样操作。对于再将弯线型弄直的过程中，由于他是一个二叉树，所以要将父亲和儿子的值给交换一下，这样子才可以让其维持二叉树的特点。

那么这种最基本的情况讲完了，但是这并不足以应付一些复杂的情况，如果说存在子树的话，那么怎么去移动父亲，儿子，爷爷三个点的子树就成为了问题。

那么如下所示

对于这样子一个二叉树，我应该怎么去维护他的平衡性。可以按照如下的操作。

首先我们要先找到他的不平衡点，我们去依次标记他的子树的大小，如下所示

可以知道当前的为直线型，爷爷，父亲，儿子分别为4,7,15三个点，那么由于是直线型，那么父亲必然是要作为接下来的新根节点，但是问题是此时，由于他是在中间位置，如果我直接去做弯折的操作，就会导致他的子树无法处理（总不能直接变成三叉树吧），所以这个时候，我需要做的是对他的子树进行转移。

如何转移他的子树呢，对于由于此时爷爷节点在下移了之后，他的位置有一个子树的位置是空了，所以在这里可以把子树转移到他的爷爷节点下面，转移之后，如下所示

实际上，我们就是将节点转移到了爷爷上面，并且把父亲作为了新的根节点。

那么对于有子树的弯折型，又应该怎么处理呢，可以参考如下的例子。在这里，已经标记好了弯折点。

在这里，接下来要做的就是去首先将它给掰直，在掰直的过程中，可以发现由于16的存在，影响了掰直，所以在这里的处理措施是将将7移动到与6连接的地方，在这之后，就是将15节点移动下来，并将14节点拼接到15节点上，这样，就完成了一次移动，完成后的结果如下所示。
之后，我们可以看到他接下来就可以弄弯了。

这样子，我们就可以实现对他的平衡的维护了。

最后总结一下吧。

1.对于直线型，我们要做的是将它儿子的那个不在线上的子树给他的父亲节点，这样子就可以完成平衡的维护

2.对于弯线型，则可以去将其儿子的子树给到父亲节点，然后将儿子放在中间位置，在这之后，就是做和直线型一样的操作。