傅里叶级数 转自 https://zhuanlan.zhihu.com/p/609597010
傅里叶级数的公式:
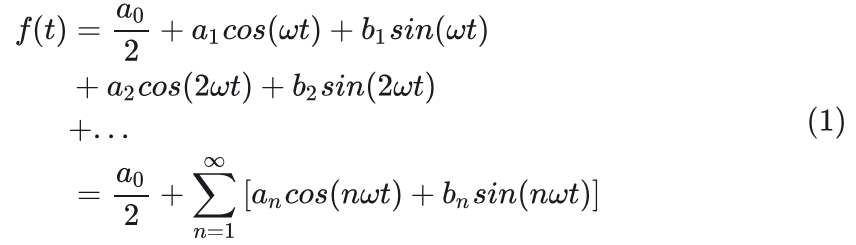
其中:
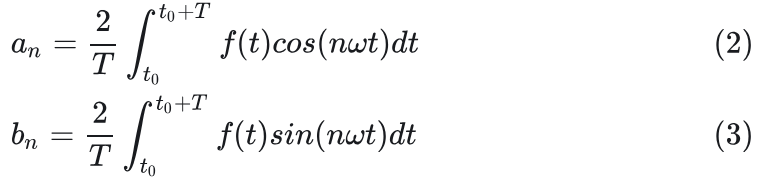
为了积分方便,积分区间一般设为[-π, π],也相当一个周期T的宽度。
1、把一个周期函数表示成三角级数:
首先,周期函数是客观世界中周期运动的数学表述,如物体挂在弹簧上作简谐振动、单摆振动、无线电电子振荡器的电子振荡等,大多可以表述为:

这里 t 表示时间, A 表示振幅, w 为角频率, Ψ为初相(与考察时设置原点位置有关,可以理解为一个常量)。
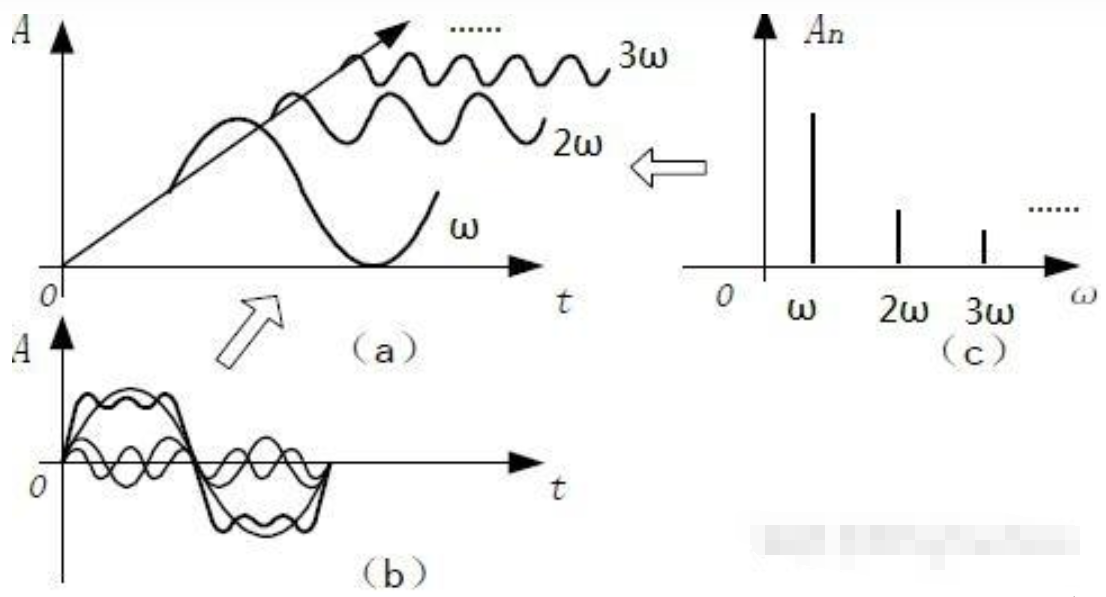
然而,世界上许多周期信号并非正弦函数那么简单,如方波、三角波等。傅里叶就想,能否用一系列的三角函数

之和来表示那个较复杂的周期函数 f(t) ?因为正弦函数 sin 可以说是最简单的周期函数了。于是,傅里叶写出下式:
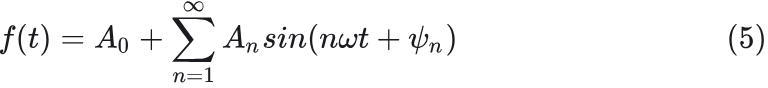
这里,t是变量,其他都是常数。与上面最简单的正弦周期函数相比,5式中多了一个n,且n从1到无穷大。这里f(t)是已知函数,也就是需要分解的原周期函数。从公式5来看,傅里叶是想把一个周期函数表示成许多正弦函数的线性叠加,这许许多多的正弦函数有着不同的幅度分量(即式中An)、有不同的周期或说是频率(是原周期函数的整数倍,即n)、有不同的初相角(即
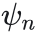
),当然还有一项常数项(即

)。要命的是,这个n是从1到无穷大,也就是是一个无穷级数。
这里强调一下,傅里叶级数中对不同频率的波有一个要求就是给定一个初始的频率
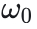
,之后的角频率必须是
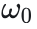
的整数倍, 这就是DTF(离散傅里叶变化)中的角频率取值的原则。
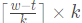






![[2025.1.13 JavaSE学习]集合-7(Hashtable Properties)](https://img2024.cnblogs.com/blog/3574171/202501/3574171-20250114033027596-1768811498.png)