[ARC070E] NarrowRectangles

前言

模拟赛 \(\rm{T4}\) , 不会比较正常, 仅仅只是记录做法

然后就是还有每日一练

思路

首先是朴素的 \(\rm{dp}\)
令 \(f_{i, j}\) 表示考虑到第 \(i\) 行, 其中这一行的左端点位置为 \(j\) 的最优花费
容易写出转移

\[f_{i, j} \gets \min_{k \in [j - len_{i - 1}, j + len_i]} f_{i - 1, k} + |j - l_i| \]

考虑优化
注意到绝对值是「凸函数」, 你把 \(f_{i, j}\) 视做 \(n\) 个函数 \(f_i(x)\) , 容易递归证得 \(f_i(x)\) 也是「凸函数」

用函数的形式表示 \(f_{i - 1}\) , 然后考虑转移

你发现转移相当于在这个函数上做一个滑动窗口, 然后求最小, 具体的

记中间那一段斜率为 \(0\) 的左右端点为 \(L, R\)

利用你的初中数学知识得到表达式

\[\begin{align*} f_i (x) \gets |x - l_i| + \begin{cases} f_{i - 1} (x + len_i) , \textrm{ case } x \in (-\infty, L - len_{i}) \\ f_{i - 1} (L) , \textrm{ case } x \in [L - len_i, R + len_{i - 1}] \\ f_{i - 1} (x - len_{i - 1}) , \textrm{ case } x \in (R + len_{i - 1}, \infty) \\ \end{cases} \end{align*} \]

你发现如果只考虑大括号, 就是一个对 \(L, R\) 的偏移, 使得中间斜率为 \(0\) 的部分拉长, 然后两边扩张

具体为什么 : 左加右减常数项, 上加下减自变量

考虑加上绝对值
首先不难证明, 绝对值函数由 \(k = -1, 1\) 的一次函数拼成, 可以看做对 \(x = l_i\) 左侧的 \(k \gets k - 1\) , 对 \(x = l_i\) 右侧的 \(k \gets k + 1\)

考虑其影响, 你发现对 \(l_i\) 两侧的斜率 \(\pm 1\) 并不好维护
你发现斜率 \(\pm 1\) , 如果 \(l_i\) 恰好在原来的端点上, 会保持一个优美的性质: 相邻两线段 \(k\) 值相差为 \(1\)
考虑维护每一个斜率对应的线段的左右端点, 你会发现 \(l_i\) 不在端点上时, 会出现相邻两线段 \(k\) 相差 \(2\) 的情况, 怎么办
大胆令 \(x = l_i\) 这个点的斜率为相邻两线段的 \(k\) 中间值, 于是满足了这个美丽性质

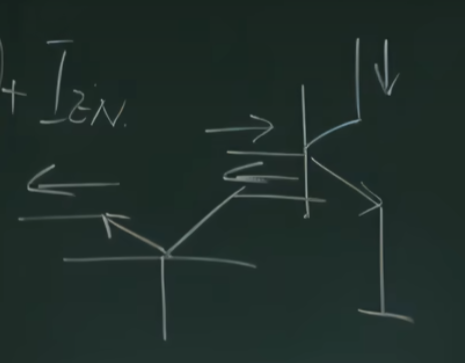
由上, 我们把 \(L\) 左侧以及 \(L\) 的线段端点 (上面的图中的红色点) 放到一块, 把 \(R\) 右侧以及 \(R\) 的线段端点放到一块, 一会解释为什么

那么我们现在大可以把 \(f_i \gets f_{i - 1}\) 分成两次操作

• 处理斜率的变化, 会产生新的左右端点
• 处理 \(L, R\) 的偏移

---

具体一点, 我们来模拟一些这样的过程

处理斜率的变化

对于 \(l_i < L\)

你可以看做把原来的 \(L\) , 也就是 左侧最小的线段端点 弹出 左侧线段端点 , 然后把它放进 右侧线段端点
还需要把 \(l_i\) 所处的位置看做一个新的端点放进左侧端点的集合中, 因为

大胆令 \(x = l_i\) 这个点的斜率为相邻两线段的 \(k\) 中间值, 于是满足了这个美丽性质

所以要放两个 \(l_i\) 进去, 表示左右端点

注意负数斜率 \(-1\), 在画图的时候表示为更陡

对于 \(l_i > R\)

跟上面的情况是类似的, 对称
绝对不是我懒

对于 \(L \leq l_i \leq R\)

你发现 \(l_i\) 变成了左右的同时端点, 其他的不变

处理 \(L, R\) 的偏移

显然可以处理每次操作的偏移量
这里有一个小问题, 你无法同时更新两个部分中所有的端点位置, 怎么办
很巧妙的方法是, 你每次将 \(L, R\) 还原之后插入, 然后对两个部分维护偏移量, 即可动态维护 \(L, R\) 的位置

现在可以解释为什么

我们把 \(L\) 左侧以及 \(L\) 的线段端点放到一块, 把 \(R\) 右侧以及 \(R\) 的线段端点放到一块, 一会解释为什么
首先是这样可以快速求出 \(f_i\) 的 \(L, R\) , 只需要对 \(L\) 维护大根堆, 对 \(R\) 维护小根堆即可

---

最后一个问题: 答案怎么求得

你发现最后的答案可以表示成 \(f_n (L \sim R)\) , 可惜不好维护
考虑每次操作的时候, 动态维护当前的 \(f_i (L), f_i(R)\)

---

具体怎么做?
首先需要发现偏移操作并不影响 \(y\) 值

对于上文中 \(l_i < L\) 的情况

我们可以发现这种情况下, 答案会变成 \(f_{i - 1} (L) + (L - l_i)\)

对于上文中 \(l_i > R\) 的情况

我们可以发现这种情况下, 答案会变成 \(f_{i - 1} (L) + (l_i - R)\)

对于上文中 \(L \leq l_i \leq R\) 的情况

我们可以发现这种情况下, 答案不变

---

动态维护即可

---

总结一下, 每次维护新的 \(f_i\) , 我们首先计算偏移量, 然后维护新的线段端点, 统计对答案的影响

总结

清新 \(\rm{dp}\) , 这种没有后效性的问题要多考虑 \(\rm{dp}\)

特殊性质 : 凸函数

对于特殊的操作, 比如本题中只会造成 \(k \pm 1\) 的情况, 考虑特殊维护
一般可以先找特殊性质, 然后推广到一般上

多个操作考虑分开考虑

对于这种处理 \(L_{\max}, R_{\min}\) 类问题, 堆处理是常见的, 一般分左右端点讨论

多画画图可以找到操作的性质, 需要画一些更一般的图

答案无法直接统计时, 考虑每次操作动态维护答案的变化