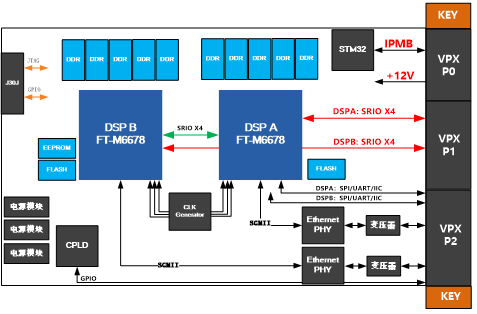
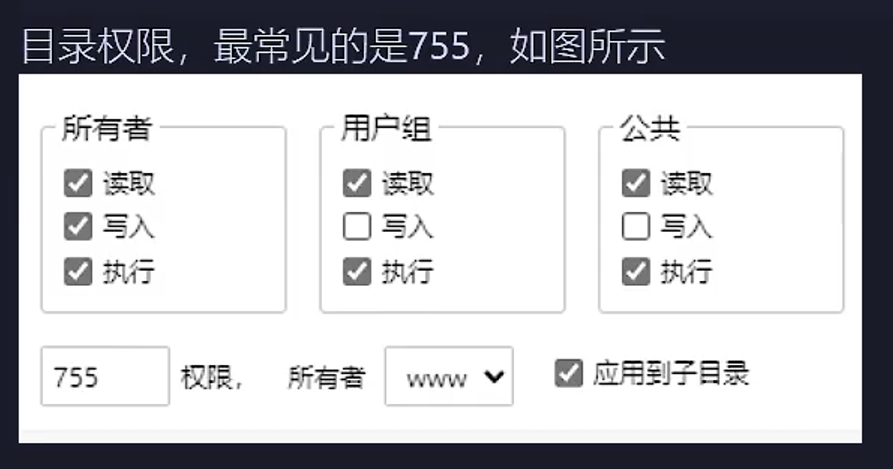
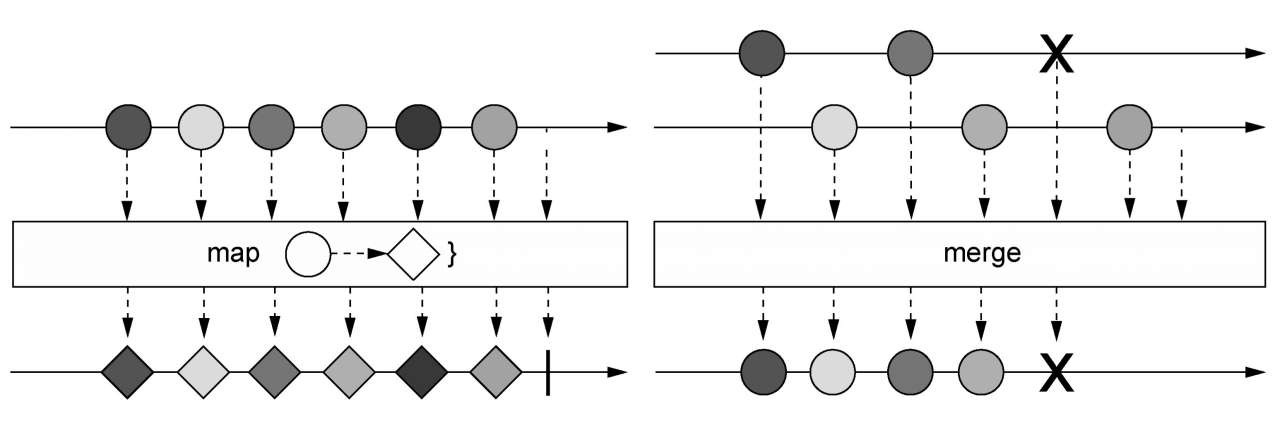
VP赛时\(4\)题,发挥得比较不错的一场,并且这场也偏简单。
A
数数题,找好规律直接模拟即可
code
B
简单排列组合题
显然总方案数为:
\(a_1到a_m\)表示某种字符的数量
想最小化总方案数,只能最大化上式分母的值。而题目操作等价于将某个\(a_i\)减\(1\),并将某个\(a_j\)加\(1\)。由全排列式的定义,显然将最小的\(a_i\)减\(1\),并将最大的\(a_j\)加\(1\)是最优的。
注意当所有\(a_i\)均相同时,若出现了超过一种字符,则要选不同的字符。
code
C
超级简单的一个div2 C题
逆向思考,计算路径和最大值,等价于计算所有没走的格子之和的最小值。而题中操作等价于可以将列任意排列,这样就相当于除了向下走的那一列,剩下的\(n-1\)列中可以不选其中任意一个数——若不选第一行的数,则该列在向下走那一列的右侧;若不选第二行的数,则该列在向下走那一列的左侧。
则直接贪心取每一列的最小值不选即可。枚举每一列作为刚开始不选的那一列,并暴力计算剩下\(n-1\)列的最小值之和即可,复杂度\(O(n^2)\)。
code
D
显然,每个元素最多只会被操作一次。(证明略)
考虑原序列:当某个元素的后面存在比它小的数时,它必然要被移动,以让后面比它小的元素移动到前面,以达到字典序最小。所以可以先通过一轮扫描来确定哪些元素一定要操作。
其次,由于某些元素移动到了后面,那些还没移动的元素后面又会出现一些新的值,而这些值即为 移动过的所有元素\(+1\)。所以需要再对所有没有移动的数扫一遍,若其值超过了移动后的所有数的最小值,则它也需要被移动。
经过以上操作后,就可以保证任意未移动的数的值均\(<=\)任意移动的数的值。将已经移动的数排个序,然后先将未移动的数顺序输出,再输出移动了的数即可。
code
E
考察比较全面的一道题,代码能力要求也比较高。
首先需要将所有点离散化,这样才能在\(O(n)\)的范围内枚举。
然后可以发现,最优解内的坐标轴\(x,y\)一定可以经过某些点(证明略)。这样,就不需要枚举离散化后\([1,n]\)上的所有数,只需要顺序枚举所有已有点的坐标即可。
考虑顺序枚举所有点的 \(x\) ,这样就将所有点分成了左右两部分。若对于任意给定的\(y\),可以知道每一侧中 \(<=y\) 的点的数量,就可以在给定的\(x,y轴\)下计算出四个象限内的点数。由于\(x\)的枚举会使某一侧增加一些点,而另一侧减少一些点,故涉及修改操作,需要用两个树状数组来维护每一侧所有点的\(y\)。而枚举\(y\)时可以利用“最小值在\(y\)上侧(一二象限)还是下侧(三四象限)”这个二段性,使用二分来枚举\(y\)。在二分函数内更新全局最优解即可。
具体细节看代码,复杂度\(O(nlog^2n)\)。
code