题面
link
【题目描述】
城市的规划在城市建设中是个大问题。
不幸的是,很多城市在开始建设的时候并没有很好的规划,城市规模扩大之后规划不合理的问题就开始显现。
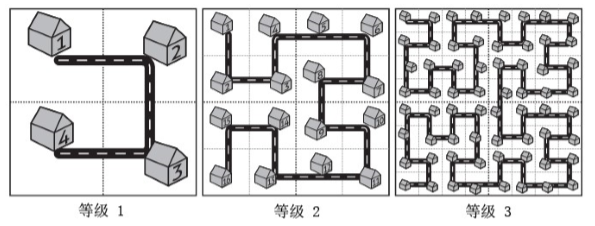
而这座名为 Fractal 的城市设想了这样的一个规划方案,如下图所示:
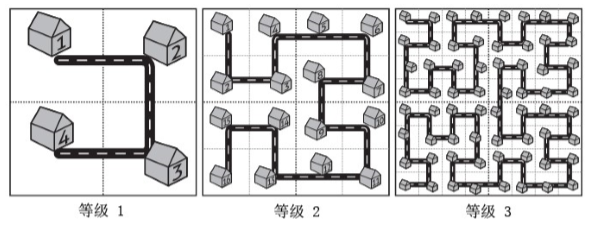
当城区规模扩大之后,Fractal 的解决方案是把和原来城区结构一样的区域按照图中的方式建设在城市周围,提升城市的等级。
对于任意等级的城市,我们把正方形街区从左上角开始按照道路标号。
虽然这个方案很烂,Fractal 规划部门的人员还是想知道,如果城市发展到了等级 \(N\),编号为 \(A\) 和 \(B\) 的两个街区的直线距离是多少。
街区的距离指的是街区的中心点之间的距离,每个街区都是边长为 \(10\) 米的正方形。
【数据范围】
\(1\le N\le31,1\le A,B\le2^{2N},1\le n\le1000\)
思路
首先这道题一眼递归,通过 \(n-1\) 级的坐标信息就可以推出 \(n\) 级的坐标信息。
那我们不妨在图形中央建系。
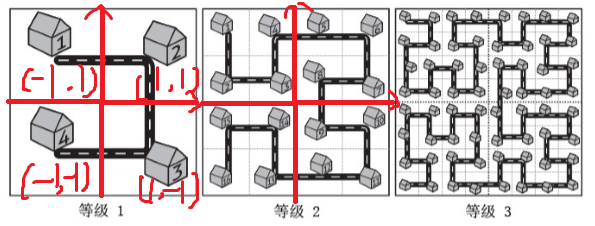
那我们接下来考虑的就是坐标信息如何转移了。
1.坐标信息的转移
首先我们需要一些数学芝士铺垫一下:
- 对于点 \((x, y)\),沿原点顺时针旋转 \(90°\),将变为 \((y, -x)\)。
- 对于点 \((x, y)\),沿原点逆时针旋转 \(90°\),将变为 \((-y, x)\)。
- 对于点 \((x, y)\),以 \(y\) 轴为对称轴翻转将变为 \((-x, y)\)。
我们直接探究等级 \(1\) 如何转等级 \(2\)
仔细观察左上角是由等级 \(1\) 顺时针旋转 \(90°\),再对 \(y\) 轴翻转而来(序号需要对应)。
右上角和右下角都是直接平移,不需要改变。

左下角是由等级 \(1\) 逆时针旋转 \(90°\),再对 \(y\) 轴翻转而来(序号需要对应)。

然后就根据象限平移就行了(具体细节见代码)。
2.计算距离
最后计算距离只需要 \(\times 5\) 而不是 \(\times 10\)。
因为原点是在图形中央的,而距离计算的是每个村庄中心点间的距离。
举个栗子:
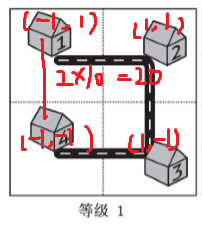
若计算 \(1\) 和 \(4\) 的距离,如果 \(\times 10\),最后答案是 \(20\),而正确答案是 \(10\)。
最后 一定要开 \(long long\)!!!要写 \(1LL\) !!!
#include<bits/stdc++.h>
#define int long long
#define PII pair<int,int>
using namespace std;
int q,n,a,b;
PII solve(int n,int m)//细节m是从0开始的
{if(n==0) return {0,0};int len=1LL<<(n-1);//象限边长 2^{n-1} 不写1LL两行泪int cnt=1LL<<(2*n-2);//象限总数 4^{n-1}PII xx=solve(n-1,m%cnt);//上一等级的坐标信息int x=xx.first,y=xx.second;int z=m/cnt;//判断处于哪个象限/*象限分布为(由等级 1 定义而来)0|1———3|20为第二象限,1为第一象限,2为第四象限,3为第三象限*/if(z==0){//(x,y)顺转90->(y,-x)翻转y轴->(-y,-x)平移->(-y-len,-x+len)return {-y-len,-x+len};}else if(z==1){//(x,y)平移->(x+len,y+len)return {x+len,y+len};}else if(z==2){//(x,y)平移->(x+len,y-len)return {x+len,y-len}; }else{//(x,y)逆转90->(-y,x)翻转y轴->(y,x)平移->(y-len,x-len)return {y-len,x-len};}
}
signed main()
{ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);cin>>q;while(q--){cin>>n>>a>>b;PII x=solve(n,a-1);//细节从0开始PII y=solve(n,b-1);double w=(double)x.first-y.first,v=(double)x.second-y.second;double ans=sqrt(w*w+v*v)*5;//距离公式 细节原点是在图形中央,所以距离只用乘5cout<<fixed<<setprecision(0)<<ans<<"\n";}return 0;
}