最近刚学完主席树,找了道题巩固一下,还是非常有收获的。
题目链接:problem
若只让求\(f(1)\),则还是比较简单的——用权值树状数组维护\(dfs\)路径上的数,每次查一下在 递归路径中\(>\)当前结点值 的结点数量,累加起来即为\(f(1)\)。
可是题目要求将\(f(1)到f(n)\)全部求出,且\(n<=2e5\),显然不能对每个点都\(dfs\)一次来求,需要利用\(f(1)\)来计算出其他答案,这显然是换根\(DP\)的思路:
设\(v\)是\(u\)的儿子(整棵树以\(1\)为根),若\(f(u)\)已知,可以推出\(f(v)\),则问题解决。

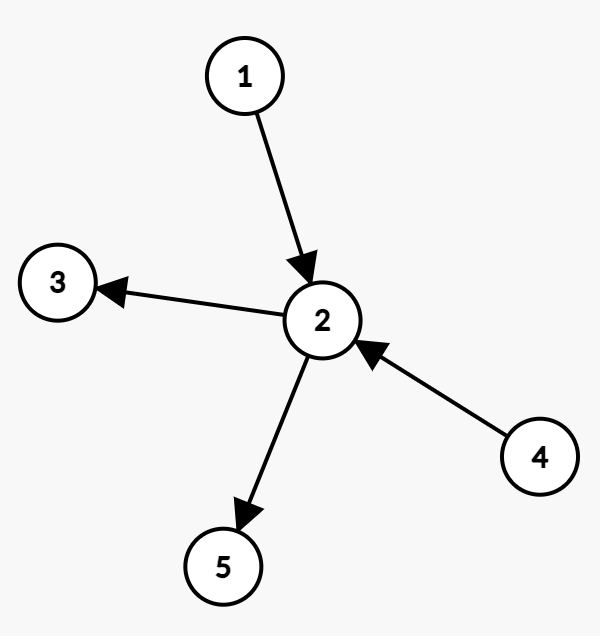
画出换根前后的两个图,可以发现:
f(3) = f(1) - 1对红色子树(包括3)的贡献 + 3对蓝色子树(包括1)的贡献
这里的贡献可以理解为逆序对的数量:
- \(1\)红:对于红色子树内的所有点\(v\),满足\(v<1\)的\(v\)的数量
(\(1\)作为\(w\))。此贡献在\(1\)下移后消失。 - \(3\)蓝:对于蓝色子树内的所有点\(v\),满足\(v<3\)的\(v\)的数量
(\(3\)作为\(w\))。此贡献在\(3\)上移后产生。而计算这个必须用
\(v - 1\)(\(<v\)的总数量)再减去红色子树中\(v<3\)的\(v\)的数量得到(注意不能用蓝色子树,因为右图是换根后的想象图,而左图中的红色子树是真实存在的)。
因此,计算\(f(u)\),只需要知道在以\(u\)为根的子树中\(<\)某个定值\(k\)的数的数量即可。
可以发现,若将子树理解为子区间,则问题就转化为:查询给定区间的任意子区间中\(<k\)的值的数量。这个问题就是主席树的板子。
而子树恰好可以映射成子区间 -> 只需要处理出\(dfn\)序,这样一棵子树就恰好对应\(dfn\)数组中的一个连续的区间,所有子树就成为了\(dfn\)数组的子区间,对这个\(dfn\)序列建好主席树,对每个点用它的父节点递推计算答案即可,复杂度\(O(nlogn)\)。
code