Prim最小生成树算法
首先给出最小生成树的概念:把给定的无向图中转换成一棵树,且树的边权和最小
Prim算法基于贪心的思想,每次在图中选取距离最小生成树最近的点加入树
首先给出朴素的模板算法:
struct edge{int v,w;
};int n,m;
vector<edge> e[5010];
int dis[5010];
bool vis[5010];
int cnt,sum;void init(void){memset(dis,0x3f,sizeof dis);
}bool prim(int s){init();dis[s]=0;while(1){int u=0;for (int i=1;i<=n;i++){if (dis[i]<dis[u]&&!vis[i])u=i;}if (u==0) break;vis[u]=1;cnt++;sum+=dis[u];for (auto it=e[u].begin();it!=e[u].end();it++){if (dis[it->v]>it->w)dis[it->v]=it->w;}}return cnt==n;
}
其中的
int u=0;
for (int i=1;i<=n;i++){if (dis[i]<dis[u]&&!vis[i])u=i;
}
if (u==0) break;
作用是找到一个距离最小生成树最近的点(这个点还没有加入树)
如果最后没有找到满足条件的点,就应该结束循环,退出 while(1)
vis[u]=1;//标记找到的这个点已经被加入树中
cnt++;//记录加入树的节点数加一
sum+=dis[u];//最小生成树的边权和
然后根据找到的这个点更新它连通的邻点到最小生成树的距离
for (auto it=e[u].begin();it!=e[u].end();it++){if (dis[it->v]>it->w)dis[it->v]=it->w;
}
这里以一个连通图为例:
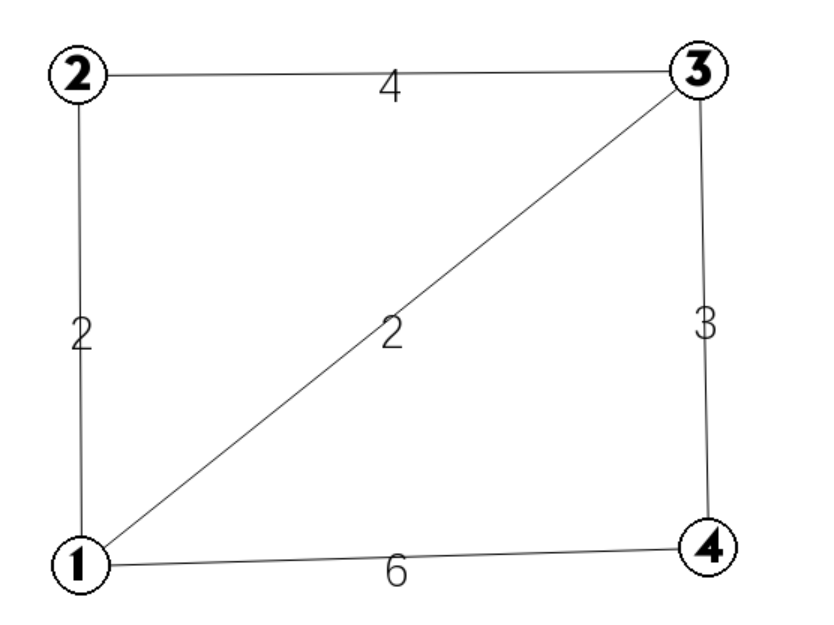
我们可以任意以一个点为 s 即起始点,s=1 时
第一轮:
树无节点,此时的dis 为 dis[]={inf,0,inf,inf,inf},从小到大找到 1 为最小点,1 加入最小生成树
然后更新 1 的邻点,dis={inf,0,2,2,6}
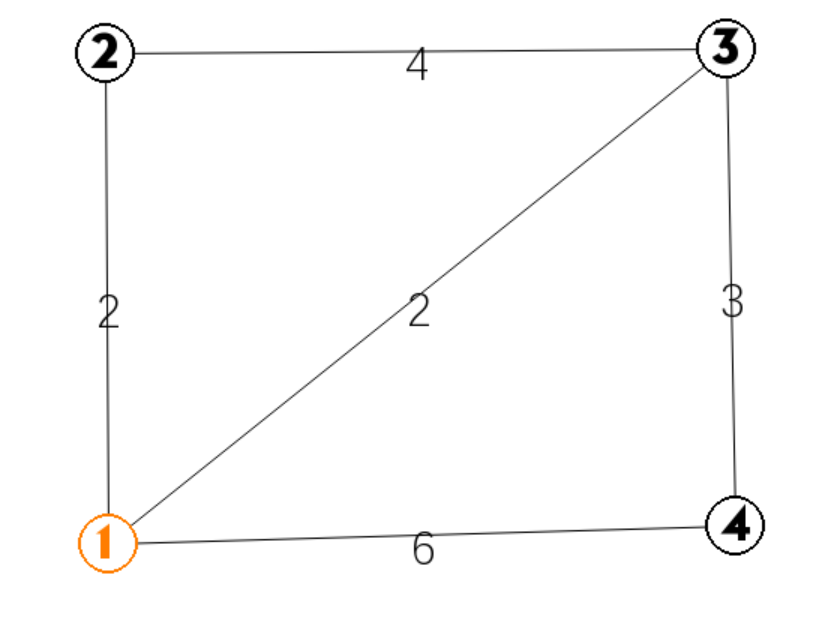
第二轮:
树节点有 1,此时的dis 为 dis[]={inf,0,2,2,6},从小到大找到 2 为最小点,2 加入最小生成树
然后更新 2 的邻点,dis={inf,0,2,2,6}
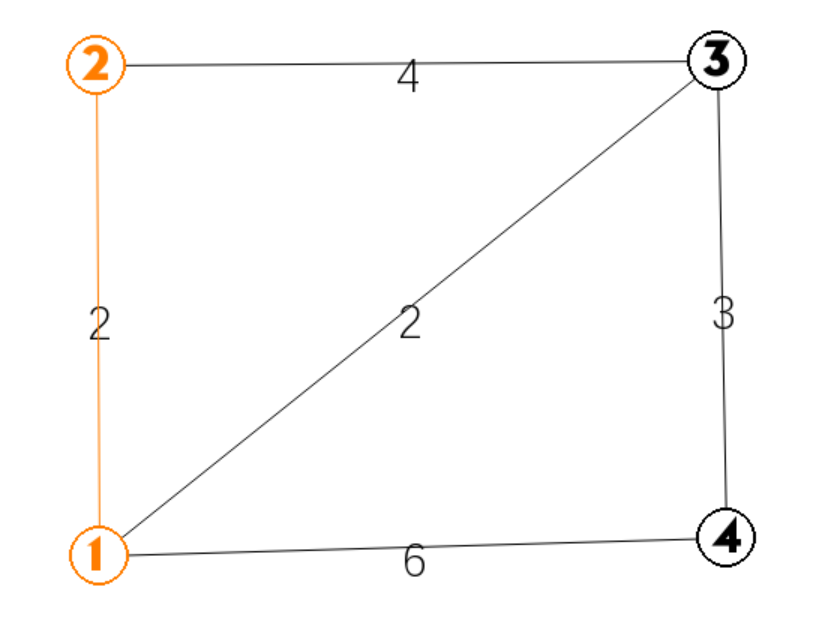
第三轮:
树节点有 1,2,此时的dis 为 dis[]={inf,0,2,2,6},从小到大找到 3 为最小点,3 加入最小生成树
然后更新 3 的邻点,dis={inf,0,2,2,3}
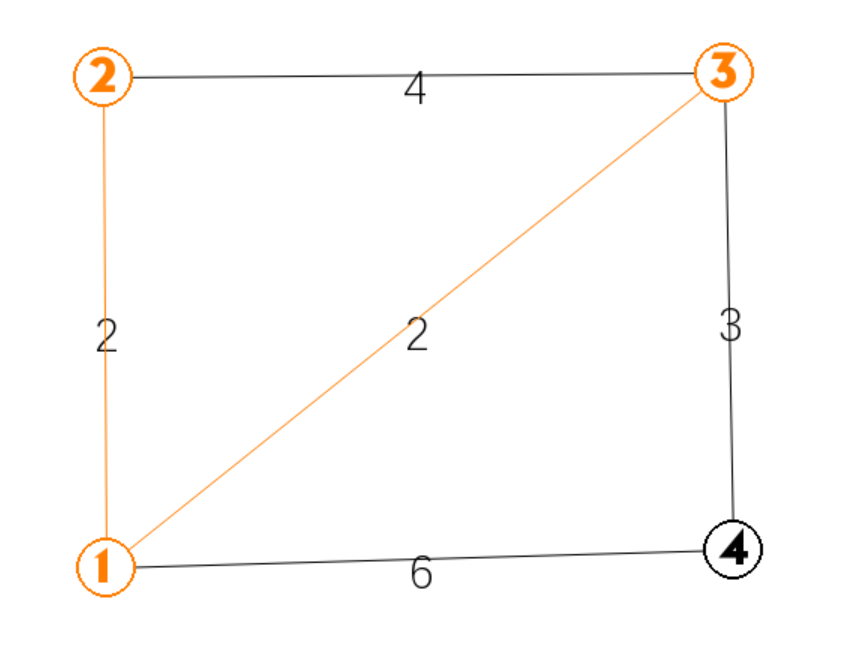
第三轮:
树节点有 1,2,3,此时的dis 为 dis[]={inf,0,2,2,3},从小到大找到 4 为最小点,4 加入最小生成树
然后更新 4 的邻点,dis={inf,0,2,2,3}
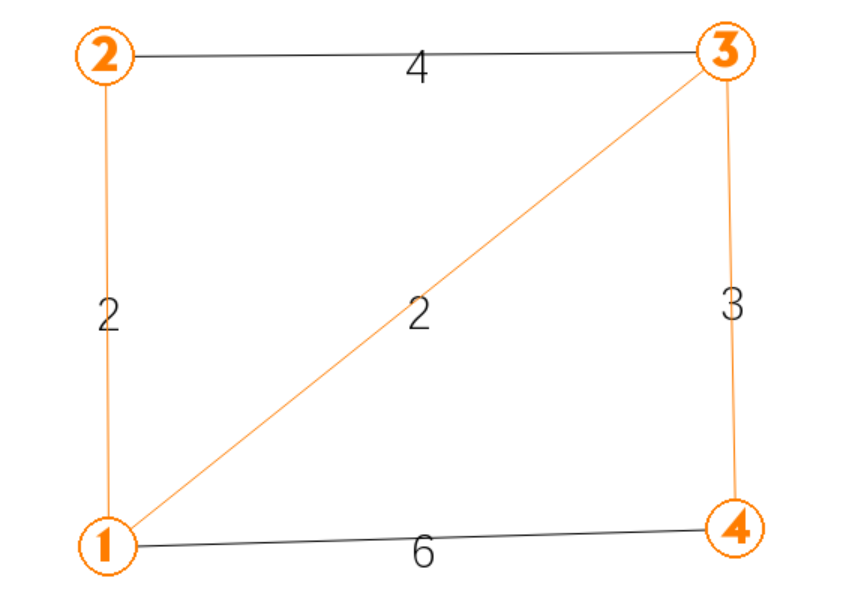
第四轮:
树节点有 1,2,3,4,此时的dis 为 dis[]={inf,0,2,2,3},找不到满足条件的点,退出循环
return cnt==n;
返回所有的点是否都加入了树,如果没有全部进树,说明存在不连通点
同样的,对于找最近点的操作可以使用 priority_queue 优先队列优化
priority_queue<pair<int,int>> q;bool prim(int s){init();dis[s]=0;q.push({0,s});while (q.size()){auto t=q.top();q.pop();if (vis[t.second]) continue;vis[t.second]=1;sum-=t.first;cnt++;for (auto it=e[t.second].begin();it!=e[t.second].end();it++){if (dis[it->v]>it->w){dis[it->v]=it->w;q.push({-dis[it->v],it->v});}}}return cnt==n;
}
使用优先队列优化后仍然不要忘记判断点和树的关系
if (vis[t.second]) continue;//如果不是没有进树的点,那就重新找
区别于最短路的问题,最小生成树更新边的关系原理不一样
for (auto it=e[u].begin();it!=e[u].end();it++){//此时的u已经进了树if (dis[it->v]>it->w)//到树的距离为dis[v]和wdis[it->v]=it->w;//取两者最小,即更新最短距离
}
在最小生成树中,把边权重新更新为 到树的最短距离,而非最短路中的到起始点的最短距离