数据结构–栈的引用–前中后缀表达式(后部分)

中缀表达式转后缀表达式(手算)
中缀转后缀 \color{purple}中缀转后缀 中缀转后缀的 手算方法 \color{purple}手算方法 手算方法:
①确定中缀表达式中 各个运算符的运算顺序 \color{red}各个运算符的运算顺序 各个运算符的运算顺序
②选择下一个运算符,按照 「左操作数右操作数运算符」 \color{red}「左操作数右操作数运算符」 「左操作数右操作数运算符」的方式组合成一个新的操作数③如果还有运算符没被处理,就继续②
“左优先”原则 \color{red}“左优先”原则 “左优先”原则:只要左边的运算符能先计算,就优先算左边的

中缀表达式转后缀表达式(机算)
初始化一个栈,用于保存 暂时还不能确定运算顺序的运算符 \color{red}暂时还不能确定运算顺序的运算符 暂时还不能确定运算顺序的运算符。从左到右处理各个元素,直到末尾。可能遇到三种情况:
①遇到 操作数 \color{red}操作数 操作数。直接加入后缀表达式。
②遇到 界限符 \color{red}界限符 界限符。遇到“(”直接入栈;遇到“)”则依次弹出栈内运算符并加入后缀表达式,直到弹出“(”为止。注意:“(”不加入后缀表达式。
③遇到 运算符 \color{red}运算符 运算符。依次弹出栈中 优先级 \color{purple}优先级 优先级高于或等于当前运算符的所有运算符,并加入后缀表达式,若碰到“(”或栈空则停止。之后再把当前运算符入栈。
∗ / 优先级高于 + − \color{pink}*/优先级高于+- ∗/优先级高于+−
按上述方法处理完所有字符后,将栈中剩余运算符依次弹出,并加入后缀表达式。

中缀表达式的计算(用栈实现)
用栈实现 \color{purple}用栈实现 用栈实现中缀表达式的计算:
初始化两个栈, 操作数栈 \color{red}操作数栈 操作数栈和 运算符栈 \color{red}运算符栈 运算符栈
若扫描到操作数,压入操作数栈
若扫描到运算符或界限符,则按照“中缀转后缀”相同的逻辑压入运算符栈(期间也会弹出运算符,每当弹出一个运算符时,就需要再 弹出两个操作数栈的栈顶元素并执行相应运算,运算结果再压回操作数栈 \color{red}弹出两个操作数栈的栈顶元素并执行相应运算,运算结果再压回操作数栈 弹出两个操作数栈的栈顶元素并执行相应运算,运算结果再压回操作数栈)
后缀表达式的计算(机算)
用栈实现 \color{purple}用栈实现 用栈实现后缀表达式的计算:
①从左往右扫描下一个元素,直到处理完所有元素②若扫描到操作数则压入栈,并回到①;否则执行③
③若扫描到运算符,则弹出两个栈顶元素,执行相应运算,运算结果压回栈顶,回到①

注意:
先出栈的是“右操作数”
栈用于存放当前暂时还不能确定运算次序的操作数
中缀表达式转后缀表达式(机算)
初始化一个栈,用于保存 暂时还不能确定运算顺序的运算符 \color{red}暂时还不能确定运算顺序的运算符 暂时还不能确定运算顺序的运算符。从左到右处理各个元素,直到末尾。可能遇到三种情况:
①遇到 操作数 \color{red}操作数 操作数。直接加入后缀表达式。
②遇到KaTeX parse error: Invalid color: '界' at position 7: \color界̲限符。遇到“(”直接入栈;遇到“)”则依次弹出栈内运算符并加入后缀表达式,直到弹出“(”为止。注意:“(”不加入后缀表达式。
③遇到 运算符 \color{red}运算符 运算符。依次弹出栈中优先级高于或等于当前运算符的所有运算符,并加入后缀表达式,若碰到“(”或栈空则停止。之后再把当前运算符入栈。
按上述方法处理完所有字符后,将栈中剩余运算符依次弹出,并加入后缀表达式。
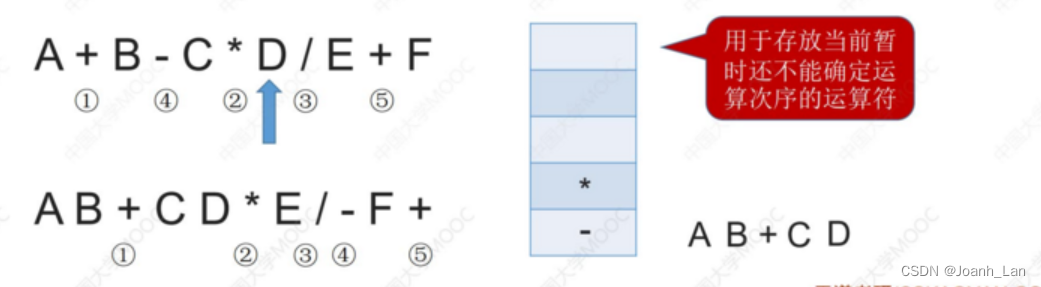
中缀表达式的计算(用栈实现)
栈实现 \color{purple}栈实现 栈实现中缀表达式的计算:
初始化两个栈, 操作数栈 \color{red}操作数栈 操作数栈和 运算符栈 \color{red}运算符栈 运算符栈若扫描到操作数,压入操作数栈
若扫描到运算符或界限符,则按照“中缀转后缀”相同的逻辑压入运算符栈(期间也会 弹出运算符,每当弹出一个运算符时,就需要再弹出两个操作数栈的栈顶元素并执行相应运算,运算结果再压回操作数栈 \color{red}弹出运算符,每当弹出一个运算符时,就需要再弹出两个操作数栈的栈顶元素并执行相应运算,运算结果再压回操作数栈 弹出运算符,每当弹出一个运算符时,就需要再弹出两个操作数栈的栈顶元素并执行相应运算,运算结果再压回操作数栈)
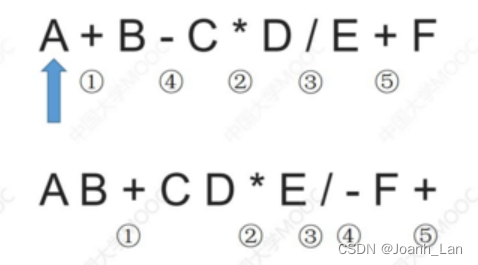
中缀表达式的计算(用栈实现)
用栈实现 \color{purple}用栈实现 用栈实现中缀表达式的计算:
初始化两个栈, 操作数栈 \color{red}操作数栈 操作数栈和 运算符栈 \color{red}运算符栈 运算符栈若扫描到操作数,压入操作数栈
若扫描到运算符或界限符,则按照“中缀转后缀”相同的逻辑压入运算符栈(期间也会 弹出运算符,每当弹出一个运算符时,就需要再弹出两个操作数栈的栈顶元素并执行相应运算,运算结果再压回操作数栈 \color{red}弹出运算符,每当弹出一个运算符时,就需要再弹出两个操作数栈的栈顶元素并执行相应运算,运算结果再压回操作数栈 弹出运算符,每当弹出一个运算符时,就需要再弹出两个操作数栈的栈顶元素并执行相应运算,运算结果再压回操作数栈)

知识点回顾与重要考点



![NSS [鹏城杯 2022]简单包含](https://img-blog.csdnimg.cn/img_convert/c48b8e11a59ae8796ecbd5d3b7e3eb79.jpeg)