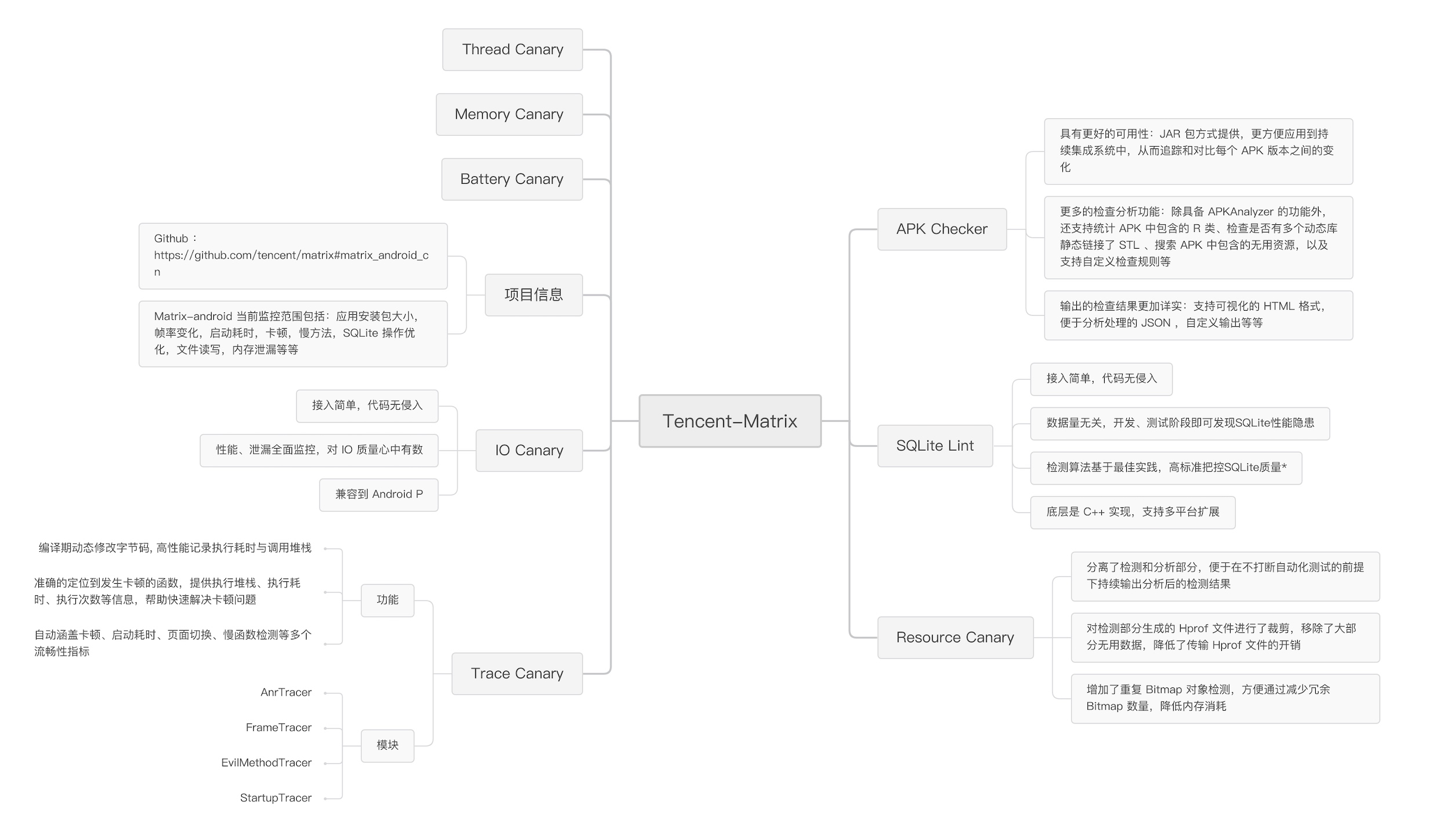
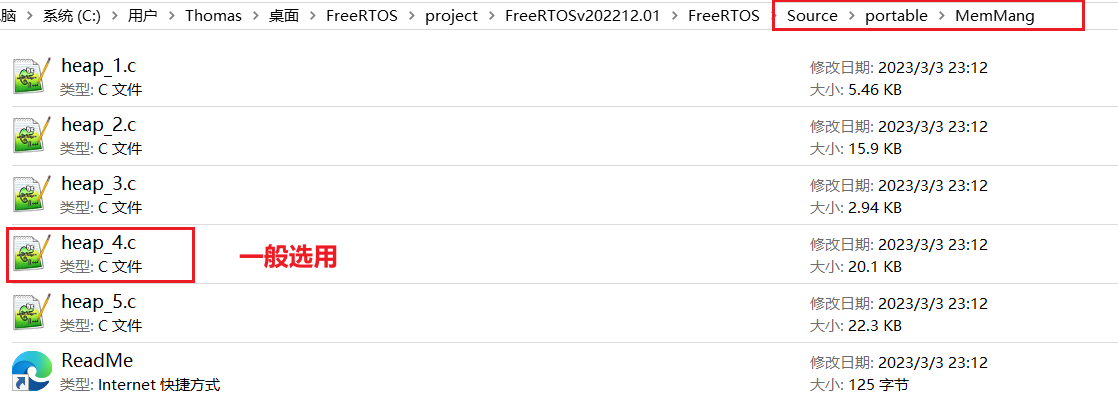
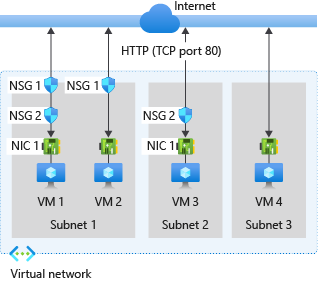
数学学到什么程度可以进行下一部分的学习了?
只要你愿意承认前面有没学懂的东西,还能心平气和地回去学懂。(而这一点是很多人做不到的,这需要内心极其强大,以及无与伦比的耐心。)
比如费曼(量子电动力学发明人之一,诺贝尔物理学奖得主)就是这样做的,转述一个在某本书里的描述,他看书就是“先一直往后看,一直看到看不下去的地方,再退回去看”,可以说是对知识点进行一个深度优先的遍历--这方法其实挺好的,在知识不是线性排列的时候尤其适用。
然而这种方法一般人有 hold 不住的危险。要用这种方法学习,必须内心强大,对自己非常诚实,心态出点偏差这人就废了。(看过费曼的传记,就会知道他是对内心非常诚实的人。)
风险之一是,不能承认自己不懂,很多概念混个脸熟就认为自己懂了。如果为了装懂而学,其实很容易把自己也忽悠进去,比如学了个新学科就满嘴名词,其实离理解还有很长距离。而且新学科里面经常有那种不太费劲的结论,比如刚看代数拓扑的时候很多结论,像球面的同调群同构于整数群之类的,直接拿过来用就能证明很多原来分析里证不了的东西(比如 Brouwer不动点定理),给人一种自己很强大的错觉。其实这只能说明工具以及工具的发明人强大,和自己的实力关系不大。新学功夫套路,总能学到点花拳绣腿,忽悠一下外行,但是有些人可能学了一年两年还在练基本功,亮不出什么花拳绣腿,但这并不是他们不如你的表现。
上面提到的例子,本质上是陷入用“熟悉” 来代替“理解”的误区。有很多事情其实解释起来非常复杂-比如煤气燃烧,火焰发出蓝色的光芒--但是因为熟悉,我们通常不会去想为什么。但是如果学习数学是这种方式,很容易把自己变成工科生的状态。(并不是说工科生不好,只是他们对数学的理解和应用的侧重点和数学系的人是不一样的。)最可怕的是,你从此适应了一种似懂非懂的状态,这个状态在学的东西比较浅的时候危害并不明显,但是很妨碍向前走。
另一种风险是,沾了看似高深的东西的皮毛,就不愿意踏踏实实学基本的内容。比如你跟富豪玩要了几天,挥金如土,像刘姥姥进大观园一样涨了点见识,还愿意去老老实实干一小时挣 50 元的辛苦活吗?能做到的话,其实见识广点挺好的,但是不能做到的话,就危险。如果虚荣心比较强,很可能会有“呀,我昨天在看泛函分析,今天退回来看线性代数里面没有掌握好的内容,会不会很丢脸”之类的想法--这种想法趁早丢掉。本来呢,知道一些好的数学,是有好处的,但是如果对心态造成了巨大的影响,就得不偿失了。
说上面这些并不是反对扩充知识面,只是做一些善意的提醒。要是想扩充点知识面,请抱着一种仰望星空的心态,仰望完了回头还得脚踏实地学习。真的扩充点知识面之后就会知道,顶尖的数学在搞星际战役,然后你学的数学就像在地球上一个宁静的小湖边上砌砖墙抹石灰--就这样你还能保持对自己的信心,相信砖墙砌好了总有一天你也能参与到星际战争里去,那就可以说心态不错了。
本科阶段跟某老师聊天,老师提到 Voevodsky 因为 motivic homotopy 的工作拿了菲尔兹奖,然后书架上拿出来 2002 年北京的国际数学家大会(ICM)的报告,翻到 Voevodsky 的一小时报告,第句里就有“triangulated category+”这个词。当时才大二,自然是不知所云。平心而论,如果有耐心和恒心,本科四年念完的时候知道 triangulated category 为何物也不错,起码北美很多学校刚入学的研究生是不知道的。如果心态摆正,看到这个概念能耐心去学(还不排除你找来一本讲triangulated category 的书,发觉上面的第一个概念也没听过的可能性),学完了发现还是搞不懂motivic homotopy theory还能有耐心去学第二句话里面的概念,那可以说这种心态已经很强大了。真是这样的话,有志者事竟成,请务必加油。(但是,你现在已经知道 triangulated category这样的词汇了,你能抵住用名词装逼的诱惑吗?)
最后,这种知识面的扩充完全应该是学有余力的情况下做的,前面提到“本科四年念完的时候知道某个概念为何物也可以说不错”,这并不是让你把自己抛下常识(比如复变函数、常微分方程、概率论、曲线和曲面的微分几何),去用这种高深的东西武装自己。诚然,很多本科的东西是十八十九世纪的数学,学完了也没什么了不起的。但是基本上只有经历了实用性(理论和工程上的)和美学的多重考验还没被淘汰掉的学科才会留在数学系的课表里面。它们本身就是简单优美的,而且是练手的好机会,能把数学上的成熟性慢慢建立起来,也有助于帮你发现自己的兴趣所在。这些学科离微积分不远,能让你看见一个抽象的概念是怎么来的,如果基础好的话,遇到困难,能退到微积分的领域,拿起纸和笔跟抽象的概念作战,则更能欣赏抽象的概念,这类从抽象到具体再到抽象的转化(也就是别人说的算例子,把一个抽象的概念拆开,转化成具体的问题算清楚,然后再用抽象的语言把结论说明白),对于成熟性的增长很有帮助。